苏教版六下数学 7.2.6立体图形的表面积和体积 教案
文档属性
| 名称 | 苏教版六下数学 7.2.6立体图形的表面积和体积 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 83.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 21:21:31 | ||
图片预览

文档简介
《立体图形的表面积和体积》复习设计
教学内容:
苏教版第十二册数学105-106页立体图形的表面积和体积
教材简析:
这是六年级第十二册数学总复习的内容。旨在让学生在整理、复习的过程中,进一步熟悉立体图形的表面积和体积的内涵,牢固掌握相关公式,能灵活地计算它们的表面积和体积,加强知识之间的内在联系,将所学知识进一步条理化和系统化。使知识向能力方面转化,为进一步发展和提高学生的空间想像能力奠定基础,为学生将来的几何学习创造条件。
本节课我以创设情景,发现问题——整理复习,构建网络——应用知识,解决问题为主要线索展开教学。注重构建知识网络,再现知识结构,深化认知水平;注重让学生灵活运用知识解决实际问题,发挥学习数学的价值;注重使不同层次的学生都有不同程度的提高,体现了复习课的实效性。
教学目标:
1、通过系统的整理、复习,使学生进一步理解、掌握立体图形的表面积和体积的意义及计算方法,加深对所学形体之间内在联系的认识。。
2、通过小组整理、实际操作等活动,培养学生的合作能力、初步的空间观念。
3、通过解决问题,感受数学与生活的密切联系,体会数学的价值。
教学重点:立体图形体积计算公式之间的联系。
教学难点:灵活利用所学知识解决简单的实际问题。
教学准备:250ml的盒装牛奶 多媒体课件
教学过程:
课前:预习提纲
1、预习相关内容,将书中一些填空部分填完整。如表面积和体积公式可以用文字或字母表示。
2、思考表面积和体积有哪些不同点,可以用表格形式进行整理,要做到有条理、层次分明。
3、思考体积公式推导过程,整理成网络图,要能体现知识间的联系。
一、创设情景,发现问题
谈话:老师今天带来了一盒同学们经常喝的牛奶(净含量250毫升的蒙牛奶),别小看它哟,里面蕴涵着很多数学问题呢, 请同学们想一想,你能根据这盒牛奶提出什么数学问题?
师:在小学阶段我们学过哪样一些立体图形?
引导:同学们想一想,工人叔叔在生产这样一盒长方体牛奶的过程中,需要考虑到哪些数学问题呢?
师:刚才同学们说的这些问题都涉及到了和表面积和体积(容积)有关方面的知识,今天这节课我们就一起来复习立体图形的表面积和体积。
二、整理复习,构建网络
(一) 建立概念
1、立体图形的表面积和体积的意义。
师提问:什么是立体图形的表面积
什么是立体图形的体积
什么是容积?
学生回忆,讨论交流,积极发言。
追问:你认为容积和体积有什么联系和区别?
联系实际:大家看,这盒牛奶上面标有净含量:250毫升,是指这盒牛奶的容积吗?
(二)小组合作,系统整理。
师:立体图形的表面积和体积的有关知识,同学们已经有所了解,下面就请同学们以小组为单位,系统地整理一下这些知识,比一比,看哪个小组整理的最好!
温馨提示:
1、试着用你们喜欢的方式来整理。
2、整理的结果要有条理、层次要分明。
3、整理的结果要能体现知识间的联系与区别。
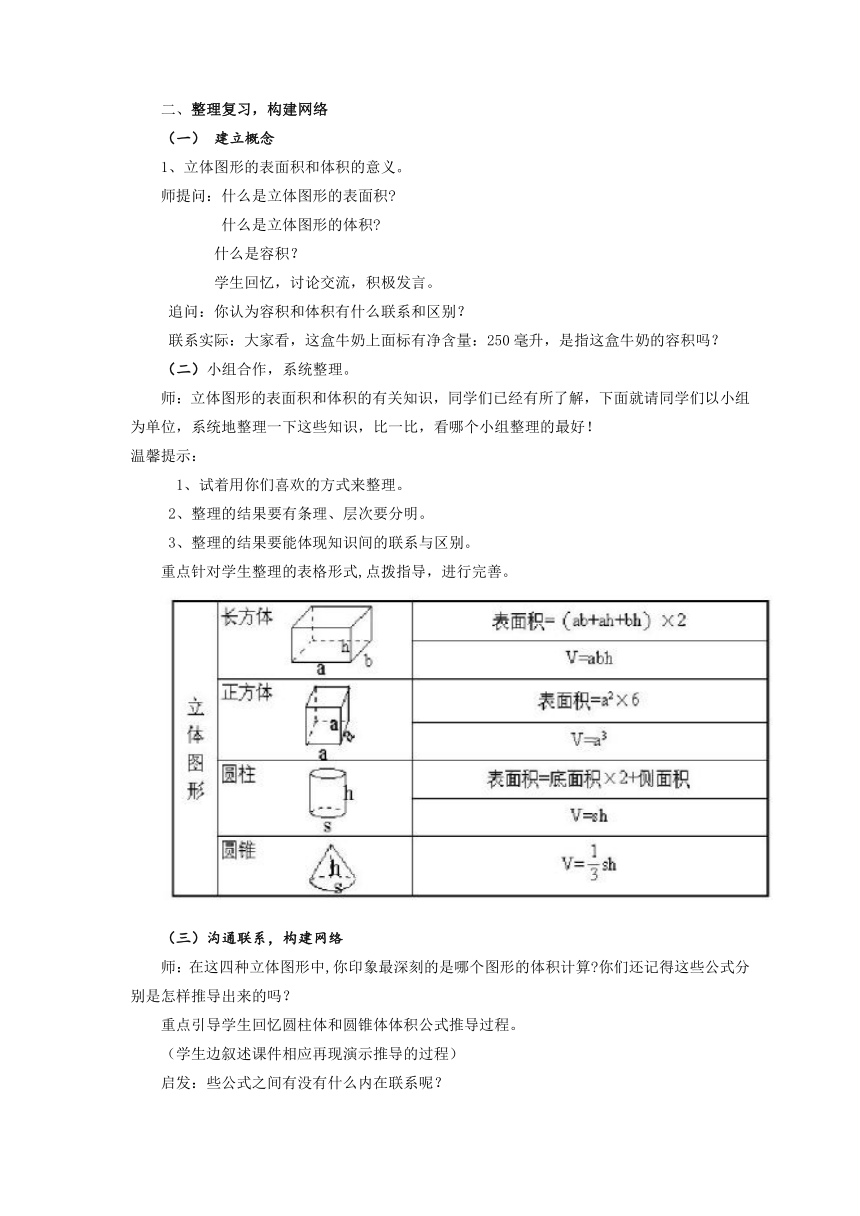
重点针对学生整理的表格形式,点拨指导,进行完善。
(三)沟通联系,构建网络
师:在这四种立体图形中,你印象最深刻的是哪个图形的体积计算 你们还记得这些公式分别是怎样推导出来的吗?
重点引导学生回忆圆柱体和圆锥体体积公式推导过程。
(学生边叙述课件相应再现演示推导的过程)
启发:些公式之间有没有什么内在联系呢?
引导回答:我们把圆柱体转化成了长方体,圆锥体转化成了圆柱体,正方体是特殊的长方体,可以直接利用长方体公式推导。
课件出示:
2:长方体、正方体、圆柱体的体积都可以用底面积乘以高来求。圆锥体的体积还要乘以三分之一。
课件出示:
师:从体积计算公式的推导过程中,我们不难发现有一个共同的特点:新问题都可以转化成已学过的知识,从而得到解决。这种转化的方法、转化的思想,是我们今后学习数学中一种很常见、很重要的方法。
三、应用知识,解决问题
师:刚才我们对立体图形的表面积和体积进行了回忆和梳理,如果要知道这盒牛奶至少需要多少平方厘米包装材料?(接头处不考虑)体积是多少立方厘米?需要搜集那些数据?怎样计算?
生:需要知道长方体牛奶盒的长、宽、高,然后可以直接利用公式进行计算。
生测量出所需要的数据,然后独立解答并集体交流。
师:五一促销活动中,蒙牛配送中心实行了“买一送二”的活动(买一件牛奶送两盒牛奶)
1、选一选 如果这两盒牛奶需要用礼品纸包装,怎样包装用的纸最节省?
(电脑显示三种不同的包装方案)
师: 喜旺配送中心也实行了有奖促销“买一送一”的活动(买一件牛奶送一个无盖圆柱形玻璃杯)
2、算一算 玻璃杯的底面半径是3厘米,高是6厘米,制造这样一个杯子大约需要多少平方厘米的玻璃?(得数保留整数)
3、想一想 请你给这个玻璃杯设计一个用料最节省的包装盒,这个包装盒的长、宽、高分别是多少厘米 它是什么形状的 这个包装盒的表面积是多少平方厘米?体积是多少?
4、倒一倒
A、如果把你手中的牛奶盒中的牛奶全部倒入一个内直径6厘米,高9厘米的圆柱形玻璃杯中,能装满吗?为什么?
B、如果把你手中的牛奶盒中的牛奶全部倒入一个底面周长18、84厘米,高10厘米的圆锥形高脚杯中,大约装几杯?
四、课堂小结:
这节课你有什么收获
教学内容:
苏教版第十二册数学105-106页立体图形的表面积和体积
教材简析:
这是六年级第十二册数学总复习的内容。旨在让学生在整理、复习的过程中,进一步熟悉立体图形的表面积和体积的内涵,牢固掌握相关公式,能灵活地计算它们的表面积和体积,加强知识之间的内在联系,将所学知识进一步条理化和系统化。使知识向能力方面转化,为进一步发展和提高学生的空间想像能力奠定基础,为学生将来的几何学习创造条件。
本节课我以创设情景,发现问题——整理复习,构建网络——应用知识,解决问题为主要线索展开教学。注重构建知识网络,再现知识结构,深化认知水平;注重让学生灵活运用知识解决实际问题,发挥学习数学的价值;注重使不同层次的学生都有不同程度的提高,体现了复习课的实效性。
教学目标:
1、通过系统的整理、复习,使学生进一步理解、掌握立体图形的表面积和体积的意义及计算方法,加深对所学形体之间内在联系的认识。。
2、通过小组整理、实际操作等活动,培养学生的合作能力、初步的空间观念。
3、通过解决问题,感受数学与生活的密切联系,体会数学的价值。
教学重点:立体图形体积计算公式之间的联系。
教学难点:灵活利用所学知识解决简单的实际问题。
教学准备:250ml的盒装牛奶 多媒体课件
教学过程:
课前:预习提纲
1、预习相关内容,将书中一些填空部分填完整。如表面积和体积公式可以用文字或字母表示。
2、思考表面积和体积有哪些不同点,可以用表格形式进行整理,要做到有条理、层次分明。
3、思考体积公式推导过程,整理成网络图,要能体现知识间的联系。
一、创设情景,发现问题
谈话:老师今天带来了一盒同学们经常喝的牛奶(净含量250毫升的蒙牛奶),别小看它哟,里面蕴涵着很多数学问题呢, 请同学们想一想,你能根据这盒牛奶提出什么数学问题?
师:在小学阶段我们学过哪样一些立体图形?
引导:同学们想一想,工人叔叔在生产这样一盒长方体牛奶的过程中,需要考虑到哪些数学问题呢?
师:刚才同学们说的这些问题都涉及到了和表面积和体积(容积)有关方面的知识,今天这节课我们就一起来复习立体图形的表面积和体积。
二、整理复习,构建网络
(一) 建立概念
1、立体图形的表面积和体积的意义。
师提问:什么是立体图形的表面积
什么是立体图形的体积
什么是容积?
学生回忆,讨论交流,积极发言。
追问:你认为容积和体积有什么联系和区别?
联系实际:大家看,这盒牛奶上面标有净含量:250毫升,是指这盒牛奶的容积吗?
(二)小组合作,系统整理。
师:立体图形的表面积和体积的有关知识,同学们已经有所了解,下面就请同学们以小组为单位,系统地整理一下这些知识,比一比,看哪个小组整理的最好!
温馨提示:
1、试着用你们喜欢的方式来整理。
2、整理的结果要有条理、层次要分明。
3、整理的结果要能体现知识间的联系与区别。
重点针对学生整理的表格形式,点拨指导,进行完善。
(三)沟通联系,构建网络
师:在这四种立体图形中,你印象最深刻的是哪个图形的体积计算 你们还记得这些公式分别是怎样推导出来的吗?
重点引导学生回忆圆柱体和圆锥体体积公式推导过程。
(学生边叙述课件相应再现演示推导的过程)
启发:些公式之间有没有什么内在联系呢?
引导回答:我们把圆柱体转化成了长方体,圆锥体转化成了圆柱体,正方体是特殊的长方体,可以直接利用长方体公式推导。
课件出示:
2:长方体、正方体、圆柱体的体积都可以用底面积乘以高来求。圆锥体的体积还要乘以三分之一。
课件出示:
师:从体积计算公式的推导过程中,我们不难发现有一个共同的特点:新问题都可以转化成已学过的知识,从而得到解决。这种转化的方法、转化的思想,是我们今后学习数学中一种很常见、很重要的方法。
三、应用知识,解决问题
师:刚才我们对立体图形的表面积和体积进行了回忆和梳理,如果要知道这盒牛奶至少需要多少平方厘米包装材料?(接头处不考虑)体积是多少立方厘米?需要搜集那些数据?怎样计算?
生:需要知道长方体牛奶盒的长、宽、高,然后可以直接利用公式进行计算。
生测量出所需要的数据,然后独立解答并集体交流。
师:五一促销活动中,蒙牛配送中心实行了“买一送二”的活动(买一件牛奶送两盒牛奶)
1、选一选 如果这两盒牛奶需要用礼品纸包装,怎样包装用的纸最节省?
(电脑显示三种不同的包装方案)
师: 喜旺配送中心也实行了有奖促销“买一送一”的活动(买一件牛奶送一个无盖圆柱形玻璃杯)
2、算一算 玻璃杯的底面半径是3厘米,高是6厘米,制造这样一个杯子大约需要多少平方厘米的玻璃?(得数保留整数)
3、想一想 请你给这个玻璃杯设计一个用料最节省的包装盒,这个包装盒的长、宽、高分别是多少厘米 它是什么形状的 这个包装盒的表面积是多少平方厘米?体积是多少?
4、倒一倒
A、如果把你手中的牛奶盒中的牛奶全部倒入一个内直径6厘米,高9厘米的圆柱形玻璃杯中,能装满吗?为什么?
B、如果把你手中的牛奶盒中的牛奶全部倒入一个底面周长18、84厘米,高10厘米的圆锥形高脚杯中,大约装几杯?
四、课堂小结:
这节课你有什么收获
