湘教版数学八年级下册同步2.7 正方形课件(18张ppt)
文档属性
| 名称 | 湘教版数学八年级下册同步2.7 正方形课件(18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-20 07:25:52 | ||
图片预览




文档简介
(共18张PPT)
第2章 四边形
2.7 正方形
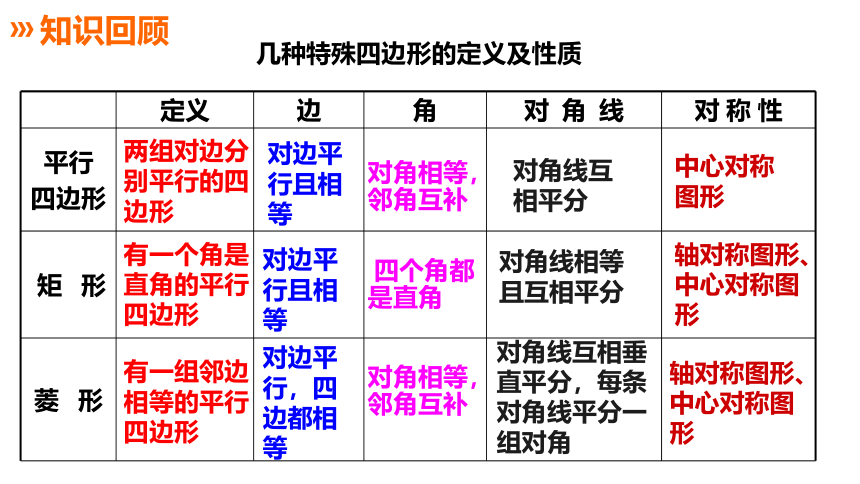
定义 边 角 对 角 线 对 称 性
平行 四边形
矩 形
菱 形
几种特殊四边形的定义及性质
对边平行且相等
对边平行且相等
对边平行,四边都相等
对角相等,邻角互补
四个角都是直角
对角相等,邻角互补
对角线互相平分
对角线相等且互相平分
对角线互相垂直平分,每条对角线平分一组对角
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、中心对称图形
两组对边分别平行的四边形
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
知识回顾
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
情景导入
〃
〃
问题1:矩形怎样变化后就成了正方形呢 你有什么发现?
正方形
讲授新课
矩 形
有一组邻边相等
问题2 菱形怎样变化后就成了正方形呢 你有什么发现?
正方形
菱形
有一个角是直角
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
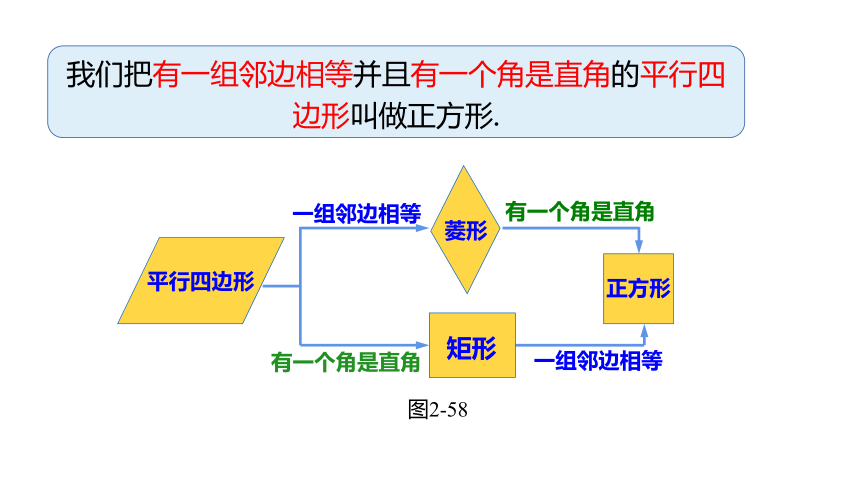
平行四边形
菱形
正方形
矩形
图2-58
我们把有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
性质:1.正方形的四条边都相等,四个角都是直角.
2.正方形的对角线相等且互相垂直平分.
结论
正方形是中心对称图形,对角线的交点是它的对称中心.
正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴.
由于正方形既是菱形,又是矩形,因此:
A
B
C
D
例1 如图2-59,点E是正方形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F.
求证:DE = DF.
∴ AD = CD, ∠A =∠DCF = 90°.
证明
∵ 四边形ABCD为正方形,
∵ DF⊥DE,
∴ ∠EDF = 90°, 即∠1 +∠3 = 90°,
图2-59
例题讲解
又 ∵ ∠2 +∠3 = 90°,
∴ ∠1 =∠2.
∴ △AED≌△CFD (ASA).
∴ DE = DF.
观察示意图2-58,说一说如何判断一个四边形是正方形?
可以先判定四边形是矩形,再判定这个矩形有一组邻边相等.
也可以先判定四边形是菱形,再判定这个菱形有一个角是直角.
探究
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
平行四边形
菱形
正方形
矩形
讲授新课
例2 如图2-60, 已知点A′,B′, C′, D′分别是正方形ABCD 四条边上的点, 并且AA′= BB′= CC′= DD′.
求证:四边形A′B′C′D′是正方形.
图2-60
证明
∵ 四边形ABCD为正方形,
∴ AB = BC = CD = DA.
又∵ AA′ = BB′ = CC′ = DD′,
∴ D′A = A′B = B′C = C′D.
又∵ ∠A =∠B =∠C =∠D = 90°,
∴ △AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
例题讲解
∴ A′D′= B′A′= C′B′= D′C′.
∴ 四边形A′B′C′D′是菱形.
又∵ ∠1 =∠3, ∠1 +∠2 = 90°,
∴ ∠2 +∠3 = 90°.
∴ ∠D′A′B′= 90°.
∴ 四边形A′B′C′D′是正方形.
图2-60
4
1
有一个角是直角或对角线相等
随堂演练
4. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF.
求证:△ABE≌△BCF.
证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠C=90°.
在△ABE和△BCF中,AB=BC,∠ABE=∠C, BE=CF
∴△ABE≌△BCF.
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形
性质
定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
课堂小结
判定
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
平行四
边形
菱形
正方形
矩形
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
正方形的判定小结
第2章 四边形
2.7 正方形
定义 边 角 对 角 线 对 称 性
平行 四边形
矩 形
菱 形
几种特殊四边形的定义及性质
对边平行且相等
对边平行且相等
对边平行,四边都相等
对角相等,邻角互补
四个角都是直角
对角相等,邻角互补
对角线互相平分
对角线相等且互相平分
对角线互相垂直平分,每条对角线平分一组对角
中心对称图形
轴对称图形、
中心对称图形
轴对称图形、中心对称图形
两组对边分别平行的四边形
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
知识回顾
观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
情景导入
〃
〃
问题1:矩形怎样变化后就成了正方形呢 你有什么发现?
正方形
讲授新课
矩 形
有一组邻边相等
问题2 菱形怎样变化后就成了正方形呢 你有什么发现?
正方形
菱形
有一个角是直角
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
平行四边形
菱形
正方形
矩形
图2-58
我们把有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
矩形
菱形
正
方
形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以矩形、菱形有的性质,正方形都有.
平行四边形、矩形、菱形、正方形之间关系:
性质:1.正方形的四条边都相等,四个角都是直角.
2.正方形的对角线相等且互相垂直平分.
结论
正方形是中心对称图形,对角线的交点是它的对称中心.
正方形是轴对称图形,两条对角线所在直线,以及过每一组对边中点的直线都是它的对称轴.
由于正方形既是菱形,又是矩形,因此:
A
B
C
D
例1 如图2-59,点E是正方形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F.
求证:DE = DF.
∴ AD = CD, ∠A =∠DCF = 90°.
证明
∵ 四边形ABCD为正方形,
∵ DF⊥DE,
∴ ∠EDF = 90°, 即∠1 +∠3 = 90°,
图2-59
例题讲解
又 ∵ ∠2 +∠3 = 90°,
∴ ∠1 =∠2.
∴ △AED≌△CFD (ASA).
∴ DE = DF.
观察示意图2-58,说一说如何判断一个四边形是正方形?
可以先判定四边形是矩形,再判定这个矩形有一组邻边相等.
也可以先判定四边形是菱形,再判定这个菱形有一个角是直角.
探究
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
平行四边形
菱形
正方形
矩形
讲授新课
例2 如图2-60, 已知点A′,B′, C′, D′分别是正方形ABCD 四条边上的点, 并且AA′= BB′= CC′= DD′.
求证:四边形A′B′C′D′是正方形.
图2-60
证明
∵ 四边形ABCD为正方形,
∴ AB = BC = CD = DA.
又∵ AA′ = BB′ = CC′ = DD′,
∴ D′A = A′B = B′C = C′D.
又∵ ∠A =∠B =∠C =∠D = 90°,
∴ △AA′D′≌△BB′A′≌△CC′B′≌△DD′C′.
例题讲解
∴ A′D′= B′A′= C′B′= D′C′.
∴ 四边形A′B′C′D′是菱形.
又∵ ∠1 =∠3, ∠1 +∠2 = 90°,
∴ ∠2 +∠3 = 90°.
∴ ∠D′A′B′= 90°.
∴ 四边形A′B′C′D′是正方形.
图2-60
4
1
有一个角是直角或对角线相等
随堂演练
4. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且BE=CF.
求证:△ABE≌△BCF.
证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠C=90°.
在△ABE和△BCF中,AB=BC,∠ABE=∠C, BE=CF
∴△ABE≌△BCF.
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形
性质
定义
有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
课堂小结
判定
有一个角是直角
一组邻边相等
一组邻边相等
有一个角是直角
平行四
边形
菱形
正方形
矩形
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
正方形的判定小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
