湘教版数学八年级下册4.2一次函数 同步课件 (共15张PPT)
文档属性
| 名称 | 湘教版数学八年级下册4.2一次函数 同步课件 (共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 282.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 09:27:26 | ||
图片预览





文档简介
(共15张PPT)
第4章 一次函数
4.2 一次函数
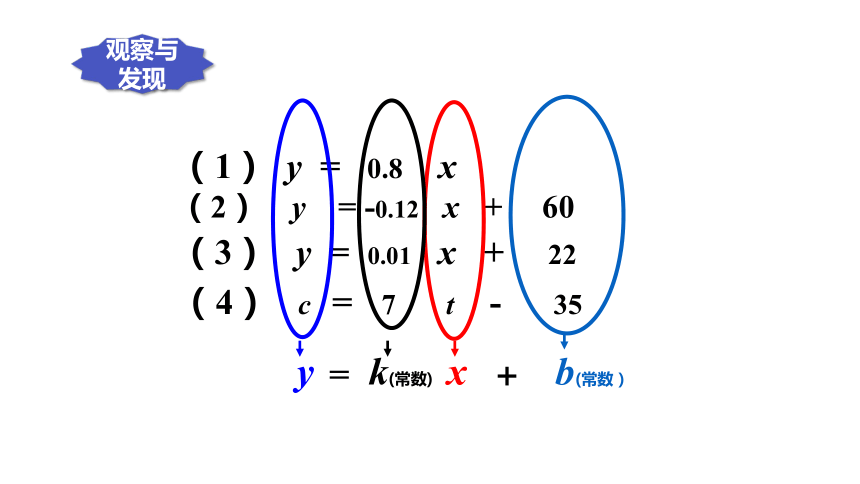
写出下列各题的函数关系式:
复习导入
(1)某地电费的单价为0.8元/(kW·h), 请用表达式表示电费y(元)与所用电量x(kW·h)之间的函数关系.
y = 0.8x
(2)某辆汽车油箱中原有油60 L,汽车每行驶50km耗油6 L. 写出剩余油量y与汽车行驶里程x的函数关系.
y=60-0.12x=-0.12x+60
(3)某城市的市内电话的月收费额y(元)包括:月租费22元,拨打电话x 分的计时费(按0.01元/分收取).
y =0.01x + 22
(x ≥ 0)
(4)有人发现,在20-25o C 时,蟋蟀每分钟鸣叫次数c 与温度t (o C )有关,即c 的值大约是t 的7倍与35的差;
c = 7t - 35
(20≤t≤25)
上述四个函数表达式有什么共同特征?
(1)y = 0.8x
(3)y =0.01x + 22
(2)y=-0.12x+60
(4)c = 7t - 35
讲授新课
(2) y = -0.12 x + 60
(3) y = 0.01 x + 22
(1) y = 0.8 x
y
k(常数)
x
=
b(常数)
+
(4) c = 7 t - 35
观察与发现
一般地,形如y=kx+b (k,b 是常数,k≠0)的函数,叫做一次函数.
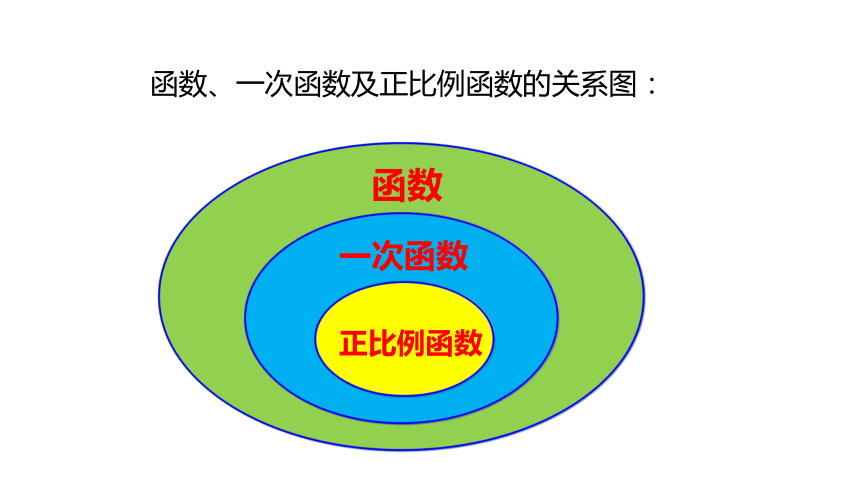
当b=0时,一次函数y=kx(k是常数,k≠0)也叫作正比例函数,其中k叫作比例系数.
正比例函数是一种特殊的一次函数
y:因变量 x:自变量 k:自变量系数 b:常数项
注意:自变量系数k与常数项b可以为数、字母、式子.
函数、一次函数及正比例函数的关系图:
函数
一次函数
正比例函数
一次函数y=kx+b(k,b为常数,k≠0)的自变量取值范围是实数集.但是在实际问题中,要根据具体情况来确定该一次函数的自变量取值范围.
注意
例如:
问题1中y = 0.8x的自变量取值范围为x ≥ 0.
问题2中y=-0.12x+60的自变量取值范围为0≤x ≤ 500.
问题3中y =0.01x + 22的自变量取值范围为x ≥ 0.
问题4中c = 7t - 35的自变量取值范围为20≤t≤25.
例1 下列关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-x-4; (2)y=5x2-6; (3)y=2πx;
(6)y=8x2+x(1-8x)
解:(1)是一次函数,不是正比例函数;
(2)不是一次函数,也不是正比例函数;
(3)是一次函数,也是正比例函数;
(4)是一次函数,也是正比例函数;
(5)不是一次函数,也不是正比例函数;
(6)是一次函数,也是正比例函数.
例题讲解
方法总结
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数项为零.
例2 科学研究发现,海平面以上10 km 以内,海拔每升高1 km,气温下降6 ℃.某时刻,若甲地地面气温为20 ℃,设高出地面x(km)处的气温为y(℃).
(1)求y(℃)随x(km)而变化的函数表达式.
(2)若有一架飞机飞过甲地上空,机舱内仪表显示飞机外面的温度为-34 ℃,求飞机离地面的高度.
解(1)高出地面的高度x(km)是自变量,高出地面x km处的气温y(℃)是x 的函数,它们之间的数量关系为甲地高出地面x km处的气温=地面气温-下降的气温,
即y = 20 - 6x.
(2)当y = -34 时,即20 - 6x = -34, 解得x = 9.
答: 此时飞机离地面的高度为9 km.
(0≤x≤10)
B
m≠2
3
一次
随堂演练
课堂小结
第4章 一次函数
4.2 一次函数
写出下列各题的函数关系式:
复习导入
(1)某地电费的单价为0.8元/(kW·h), 请用表达式表示电费y(元)与所用电量x(kW·h)之间的函数关系.
y = 0.8x
(2)某辆汽车油箱中原有油60 L,汽车每行驶50km耗油6 L. 写出剩余油量y与汽车行驶里程x的函数关系.
y=60-0.12x=-0.12x+60
(3)某城市的市内电话的月收费额y(元)包括:月租费22元,拨打电话x 分的计时费(按0.01元/分收取).
y =0.01x + 22
(x ≥ 0)
(4)有人发现,在20-25o C 时,蟋蟀每分钟鸣叫次数c 与温度t (o C )有关,即c 的值大约是t 的7倍与35的差;
c = 7t - 35
(20≤t≤25)
上述四个函数表达式有什么共同特征?
(1)y = 0.8x
(3)y =0.01x + 22
(2)y=-0.12x+60
(4)c = 7t - 35
讲授新课
(2) y = -0.12 x + 60
(3) y = 0.01 x + 22
(1) y = 0.8 x
y
k(常数)
x
=
b(常数)
+
(4) c = 7 t - 35
观察与发现
一般地,形如y=kx+b (k,b 是常数,k≠0)的函数,叫做一次函数.
当b=0时,一次函数y=kx(k是常数,k≠0)也叫作正比例函数,其中k叫作比例系数.
正比例函数是一种特殊的一次函数
y:因变量 x:自变量 k:自变量系数 b:常数项
注意:自变量系数k与常数项b可以为数、字母、式子.
函数、一次函数及正比例函数的关系图:
函数
一次函数
正比例函数
一次函数y=kx+b(k,b为常数,k≠0)的自变量取值范围是实数集.但是在实际问题中,要根据具体情况来确定该一次函数的自变量取值范围.
注意
例如:
问题1中y = 0.8x的自变量取值范围为x ≥ 0.
问题2中y=-0.12x+60的自变量取值范围为0≤x ≤ 500.
问题3中y =0.01x + 22的自变量取值范围为x ≥ 0.
问题4中c = 7t - 35的自变量取值范围为20≤t≤25.
例1 下列关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-x-4; (2)y=5x2-6; (3)y=2πx;
(6)y=8x2+x(1-8x)
解:(1)是一次函数,不是正比例函数;
(2)不是一次函数,也不是正比例函数;
(3)是一次函数,也是正比例函数;
(4)是一次函数,也是正比例函数;
(5)不是一次函数,也不是正比例函数;
(6)是一次函数,也是正比例函数.
例题讲解
方法总结
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数项为零.
例2 科学研究发现,海平面以上10 km 以内,海拔每升高1 km,气温下降6 ℃.某时刻,若甲地地面气温为20 ℃,设高出地面x(km)处的气温为y(℃).
(1)求y(℃)随x(km)而变化的函数表达式.
(2)若有一架飞机飞过甲地上空,机舱内仪表显示飞机外面的温度为-34 ℃,求飞机离地面的高度.
解(1)高出地面的高度x(km)是自变量,高出地面x km处的气温y(℃)是x 的函数,它们之间的数量关系为甲地高出地面x km处的气温=地面气温-下降的气温,
即y = 20 - 6x.
(2)当y = -34 时,即20 - 6x = -34, 解得x = 9.
答: 此时飞机离地面的高度为9 km.
(0≤x≤10)
B
m≠2
3
一次
随堂演练
课堂小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
