2.1.2 垂线 课件 (共27张PPT)
文档属性
| 名称 | 2.1.2 垂线 课件 (共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 06:22:15 | ||
图片预览







文档简介
(共27张PPT)
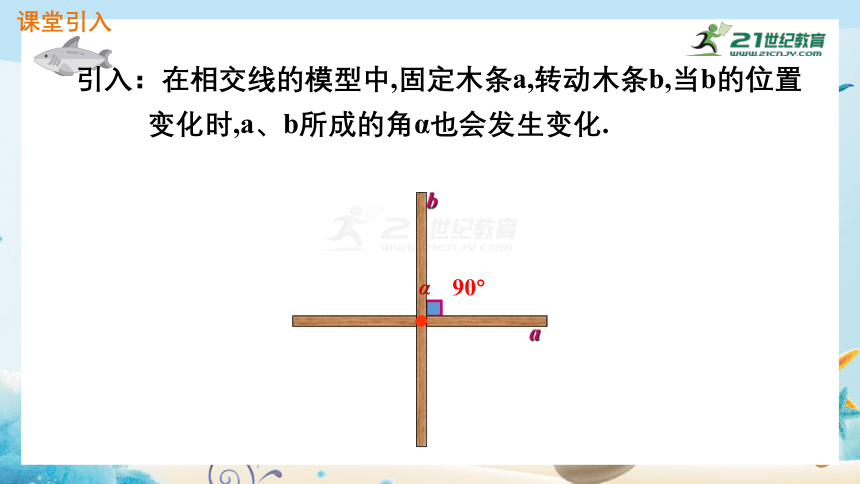
引入:在相交线的模型中,固定木条a,转动木条b,当b的位置
变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
课堂引入
a
b
α
90°
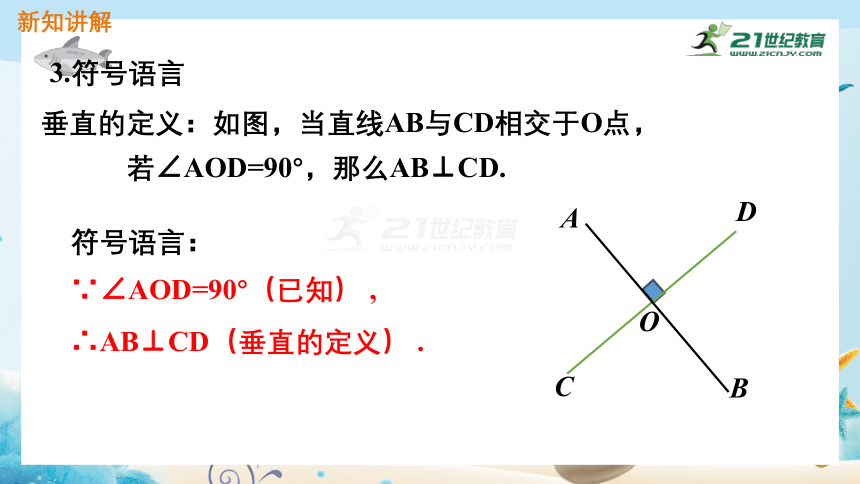
引入:在相交线的模型中,固定木条a,转动木条b,当b的位置
变化时,a、b所成的角α也会发生变化.
课堂引入
1 两条直线的位置关系
第2课时 垂线
1.了解垂直是相交的特殊情况,理解垂线的概念,会用三角板或量角器过一点画已知直线的垂线.
2.掌握点到直线的距离的概念,并会度量点到直线的距离.
3.掌握垂线的性质,并会利用所学知识进行简单的推理.
问题:
如图,当∠BOC=90°时,∠BOD、∠AOC、 ∠AOD 的度数是多少?为什么?
A
B
C
D
O
当∠BOC=90°时,
∠BOD=∠AOD=∠AOC=90°.
想一想
1、垂直的定义
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
其中的一条直线叫做另一条直线的垂线 ,它们的交点叫做垂足.
新知讲解
(1)如果直线AB与直线CD垂直,那么
可记作:AB⊥CD(或CD⊥AB).
(2)如果用a、b表示这两条直线,那
么直线a 与直线b 垂直,可记作:
a⊥b(或b⊥a).
(3)如图点O 为垂足.
A
B
C
D
O
a
b
2.垂直的表示法
“⊥”
新知讲解
A
B
C
D
O
符号语言:
垂直的定义:如图,当直线AB与CD相交于O点,
若∠AOD=90°,那么AB⊥CD.
∵∠AOD=90°(已知) ,
∴AB⊥CD(垂直的定义) .
3.符号语言
新知讲解
注意:
两条线段互相垂直是指这两条线段
所在的直线互相垂直.
新知讲解
活动一
问题1. 如图,将两根木条钉在一起,固定其中一根木条a,转动木条b,
请学生观察:在木条b的转动过程中,四个角之间有什么关系?
问题2. 当有一个角为90°时,则另外三个角的度数分别是多少?
邻补角始终互补,
对顶角始终相等.
均为90°
可借助优教平台的“【探究动画】垂线及其唯一性”互动资源,动态、直观、辅助探究与发现.
其中的一条直线叫做另一条的垂线.
记作AB⊥CD.
当两条直线相交所构成的四个角中有一个是直角时,我们就称这两条直线互相垂直.
C
A
B
D
O
垂足符号
思考:当两条直线相交,四个角相等时,这两条直线有什么位置关系?
为什么?
两条直线垂直,两条直线相交所形成的每个角都为90°.
例题.如图,直线AB、CD相交于点O,过点O作EO⊥CD,若∠EOA=50°,则∠BOD的度数是( )
A.35° B.40° C.45° D.50°
C
A
E
B
D
O
90°
50°
40°
法1:
∵EO⊥CD,
∴∠EOD=90°.
又∵点A、点O、点B在同一条直线上,
∴∠BOD=180°∠EOD∠EOA=40°.
B
例题.如图,直线AB、CD相交于点O,过点O作EO⊥CD,若∠EOA=50°,则∠BOD的度数是( )
A.35° B.40° C.45° D.50°
C
A
E
B
D
O
50°
40°
法2:
∵EO⊥CD,
∴∠EOD=90°.
∴∠EOC=180°∠EOD=90°.
∴∠AOC=90°∠EOA=40°.
∴∠BOD=∠AOC=40°(对顶角相等).
40°
B
90°
C
A
F
B
E
1
2
练习1.如图,AC⊥BC,直线EF经过点C,若∠1=37°,则∠2的度数是 .
练习2.你能举出一些生活中与垂直有关的实例吗?
53°
练习2.你能举出一些生活中与垂直有关的实例吗?
活动二
问题3. 如图,用三角尺或量角器画已知直线m的垂线,这样的垂线能画几条?
m
问题4.在一张透明的纸上画一条直线l,在l上取一点P,折出过点P与l垂直的直线.这样的直线能折出几条?过点Q呢?
l
P
Q
过P点及过Q点都只能折出1条直线与直线l垂直.
更改P点及Q点的位置,结论相同吗?
相同
尝试归纳该结论,并用严谨的数学语言描述.
无数条
在同一平面内,过一点有且只有一条直线与已知直线垂直.
存在
唯一
例题.过点P画直线l的垂线.
l
P
画垂线步骤:
一靠:令三角尺的一条直角边靠在已知直线上.
二过:沿已知直线移动三角尺,使得三角尺的
另一条直角边经过已知点.
三画:沿此直角边画直线,则这条直线就是已
知直线的垂线.
练习.如图,过P点画出已知射线AB或线段AB的垂线.
P
A
B
P
A
B
思考:如何判定两条射线垂直?两条线段呢?
两条线段垂直、两条射线垂直、射线与直线垂直、线段与射线垂直、线段与直线垂直,都是指它们所在的直线垂直.
问题5. 如图,在灌溉时,要把小溪的水引到农田P处,如何挖掘能使渠道最短?
农田和小溪分别可以抽象成几何中的什么元素?
你能用一句话概括出观察得出的结论吗?
点和直线
可借助优教平台的“【探究动画】点到直线的距离”互动资源,动态、直观、辅助探究与发现.
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
例题.如图,AC⊥BC,且BC=5,AC=12,AB=13,则点A到BC的距离是______,点B到AC的距离是_______,点B到点A的距离是_________.
A
B
C
D
5
12
13
12
5
13
1.如图,若直线a、b相交于点O,∠1=90°,则a b.
2.若直线AB、CD 相交于点O,且AB⊥CD,则∠BOD =_____.
3.如图,BO⊥AO,∠BOC与∠BOA的度数之比为1∶3,
那么∠COA=____ ,∠BOC的补角 为 .
O
a
b
1
B
C
A
O
⊥
90°
60°
150°
第1题图
第3题图
(每空10分,共80分.)
随堂练习
5.如图,点C到直线AB的距离是指( )
A.线段AC的长 B.线段CD的长
C.线段BC的长 D.线段BD的长
4.已知:如图AB⊥CD,垂足为,EF为过点O
的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余
C.互补 D.互为对顶角
B
B
随堂练习
7.如图,直线AB、CD相交于点E,EF⊥AB于点E,若∠CEF=58°,则∠BED的度数为______.
6. 如图,AD⊥AB,∠ACB=90°,线段 AC、BC、CD中最短的是( )
A.AC B.BC C.CD D.不能确定
D
A
B
C
C
C
A
B
E
F
D
32°
随堂练习
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
引入:在相交线的模型中,固定木条a,转动木条b,当b的位置
变化时,a、b所成的角α也会发生变化.
)
α
a
b
b
b
b
b
)
α
课堂引入
a
b
α
90°
引入:在相交线的模型中,固定木条a,转动木条b,当b的位置
变化时,a、b所成的角α也会发生变化.
课堂引入
1 两条直线的位置关系
第2课时 垂线
1.了解垂直是相交的特殊情况,理解垂线的概念,会用三角板或量角器过一点画已知直线的垂线.
2.掌握点到直线的距离的概念,并会度量点到直线的距离.
3.掌握垂线的性质,并会利用所学知识进行简单的推理.
问题:
如图,当∠BOC=90°时,∠BOD、∠AOC、 ∠AOD 的度数是多少?为什么?
A
B
C
D
O
当∠BOC=90°时,
∠BOD=∠AOD=∠AOC=90°.
想一想
1、垂直的定义
两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直.
其中的一条直线叫做另一条直线的垂线 ,它们的交点叫做垂足.
新知讲解
(1)如果直线AB与直线CD垂直,那么
可记作:AB⊥CD(或CD⊥AB).
(2)如果用a、b表示这两条直线,那
么直线a 与直线b 垂直,可记作:
a⊥b(或b⊥a).
(3)如图点O 为垂足.
A
B
C
D
O
a
b
2.垂直的表示法
“⊥”
新知讲解
A
B
C
D
O
符号语言:
垂直的定义:如图,当直线AB与CD相交于O点,
若∠AOD=90°,那么AB⊥CD.
∵∠AOD=90°(已知) ,
∴AB⊥CD(垂直的定义) .
3.符号语言
新知讲解
注意:
两条线段互相垂直是指这两条线段
所在的直线互相垂直.
新知讲解
活动一
问题1. 如图,将两根木条钉在一起,固定其中一根木条a,转动木条b,
请学生观察:在木条b的转动过程中,四个角之间有什么关系?
问题2. 当有一个角为90°时,则另外三个角的度数分别是多少?
邻补角始终互补,
对顶角始终相等.
均为90°
可借助优教平台的“【探究动画】垂线及其唯一性”互动资源,动态、直观、辅助探究与发现.
其中的一条直线叫做另一条的垂线.
记作AB⊥CD.
当两条直线相交所构成的四个角中有一个是直角时,我们就称这两条直线互相垂直.
C
A
B
D
O
垂足符号
思考:当两条直线相交,四个角相等时,这两条直线有什么位置关系?
为什么?
两条直线垂直,两条直线相交所形成的每个角都为90°.
例题.如图,直线AB、CD相交于点O,过点O作EO⊥CD,若∠EOA=50°,则∠BOD的度数是( )
A.35° B.40° C.45° D.50°
C
A
E
B
D
O
90°
50°
40°
法1:
∵EO⊥CD,
∴∠EOD=90°.
又∵点A、点O、点B在同一条直线上,
∴∠BOD=180°∠EOD∠EOA=40°.
B
例题.如图,直线AB、CD相交于点O,过点O作EO⊥CD,若∠EOA=50°,则∠BOD的度数是( )
A.35° B.40° C.45° D.50°
C
A
E
B
D
O
50°
40°
法2:
∵EO⊥CD,
∴∠EOD=90°.
∴∠EOC=180°∠EOD=90°.
∴∠AOC=90°∠EOA=40°.
∴∠BOD=∠AOC=40°(对顶角相等).
40°
B
90°
C
A
F
B
E
1
2
练习1.如图,AC⊥BC,直线EF经过点C,若∠1=37°,则∠2的度数是 .
练习2.你能举出一些生活中与垂直有关的实例吗?
53°
练习2.你能举出一些生活中与垂直有关的实例吗?
活动二
问题3. 如图,用三角尺或量角器画已知直线m的垂线,这样的垂线能画几条?
m
问题4.在一张透明的纸上画一条直线l,在l上取一点P,折出过点P与l垂直的直线.这样的直线能折出几条?过点Q呢?
l
P
Q
过P点及过Q点都只能折出1条直线与直线l垂直.
更改P点及Q点的位置,结论相同吗?
相同
尝试归纳该结论,并用严谨的数学语言描述.
无数条
在同一平面内,过一点有且只有一条直线与已知直线垂直.
存在
唯一
例题.过点P画直线l的垂线.
l
P
画垂线步骤:
一靠:令三角尺的一条直角边靠在已知直线上.
二过:沿已知直线移动三角尺,使得三角尺的
另一条直角边经过已知点.
三画:沿此直角边画直线,则这条直线就是已
知直线的垂线.
练习.如图,过P点画出已知射线AB或线段AB的垂线.
P
A
B
P
A
B
思考:如何判定两条射线垂直?两条线段呢?
两条线段垂直、两条射线垂直、射线与直线垂直、线段与射线垂直、线段与直线垂直,都是指它们所在的直线垂直.
问题5. 如图,在灌溉时,要把小溪的水引到农田P处,如何挖掘能使渠道最短?
农田和小溪分别可以抽象成几何中的什么元素?
你能用一句话概括出观察得出的结论吗?
点和直线
可借助优教平台的“【探究动画】点到直线的距离”互动资源,动态、直观、辅助探究与发现.
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
例题.如图,AC⊥BC,且BC=5,AC=12,AB=13,则点A到BC的距离是______,点B到AC的距离是_______,点B到点A的距离是_________.
A
B
C
D
5
12
13
12
5
13
1.如图,若直线a、b相交于点O,∠1=90°,则a b.
2.若直线AB、CD 相交于点O,且AB⊥CD,则∠BOD =_____.
3.如图,BO⊥AO,∠BOC与∠BOA的度数之比为1∶3,
那么∠COA=____ ,∠BOC的补角 为 .
O
a
b
1
B
C
A
O
⊥
90°
60°
150°
第1题图
第3题图
(每空10分,共80分.)
随堂练习
5.如图,点C到直线AB的距离是指( )
A.线段AC的长 B.线段CD的长
C.线段BC的长 D.线段BD的长
4.已知:如图AB⊥CD,垂足为,EF为过点O
的一条直线,则∠1与∠2的关系一定成立的是( )
A.相等 B.互余
C.互补 D.互为对顶角
B
B
随堂练习
7.如图,直线AB、CD相交于点E,EF⊥AB于点E,若∠CEF=58°,则∠BED的度数为______.
6. 如图,AD⊥AB,∠ACB=90°,线段 AC、BC、CD中最短的是( )
A.AC B.BC C.CD D.不能确定
D
A
B
C
C
C
A
B
E
F
D
32°
随堂练习
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
