2.3.2 平行线的性质与判定的综合运用 课件 (共31张PPT)
文档属性
| 名称 | 2.3.2 平行线的性质与判定的综合运用 课件 (共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 06:16:32 | ||
图片预览











文档简介
(共31张PPT)
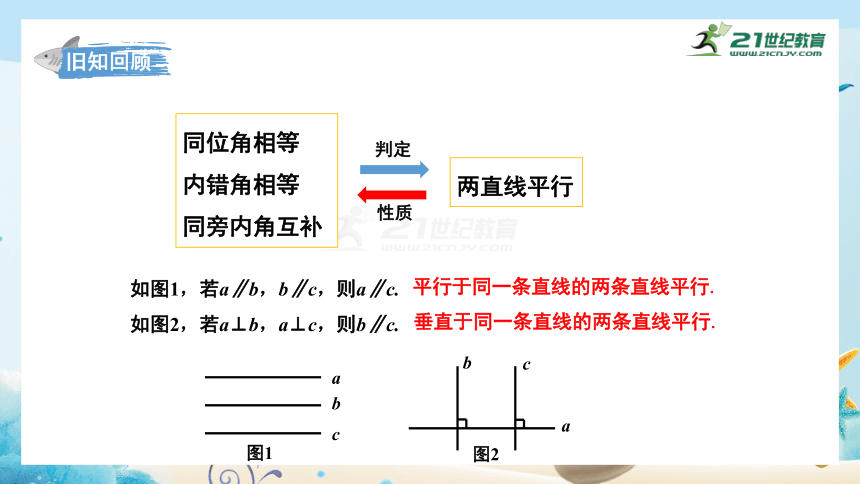
旧知回顾
问题1:判别直线平行的条件有哪几个?
你现在一共有几个判定直线平行的方法?
问题2:平行线的性质有哪几条?
问题3:在应用二者时应注意什么问题?
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
旧知回顾
如图1,若a∥b,b∥c,则a∥c.
如图2,若a⊥b,a⊥c,则b∥c.
平行于同一条直线的两条直线平行.
垂直于同一条直线的两条直线平行.
a
b
c
图1
a
b
c
图2
3 平行线的性质
第2课时 平行线的性质与判定的综合运用
学习目标
进一步掌握平行线的性质,能够根据平行线的性质与判定进行简单的推理与计算.
新知探究
1. 平行线的性质的几何符号语言
探究:如图,因为AB∥CD,
所以∠1=____( ).
因为AB∥CD,
所以∠3=____( ).
因为AB∥CD,
所以_________=180°(_____________________________).
∠2
∠2
两直线平行,同位角相等
∠4+∠2
两直线平行,同旁内角互补
两直线平行,内错角相等
新知探究
2. 如图:(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
BF∥CE
内错角相等,两直线平行
BF∥AM
同位角相等,两直线平行
AC∥MD
同旁内角互补,两直线平行
新知探究
【归纳】
由角相等或互补(数量关系)得到两条直线平行(位置关系),
这是平行线的条件;
由两条直线平行(位置关系)得到有关角相等或互补(数量关系),
这是平行线的性质.
【点拨】
平行线的条件与性质是互逆关系,解答题目时一定要区分开!
新知探究
知识点训练:平行线的性质
例:如图,AC∥BD,AE平分∠BAC 交BD于点E.
若∠1=64°,求∠2的度数.
解:由图可知∠1+∠BAC =180°,
由∠1=64°,从而求得∠BAC= 116°,
再由AE平分∠BAC,可得∠CAE =58°,
由AC∥BD,可得∠2+∠CAE =180°,
从而求得∠2=180°-58°=122°.
新知探究
【规律总结】
解决已知两直线平行,求角的关系的问题的基本思路
(1)直接法:找图中的同位角、内错角、同旁内角,进而判断它们的关系 .
(2)间接法:如果没有上述角,通过添加辅助线,构造平行线,得三类角,进而求解 .
例1 根据下图所示,回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
典型例题
∵ ∠1=∠2(已知)
∴ BF∥CE(内错角相等,两直线平行)
∵ ∠2=∠M(已知)
∴ AM∥BF(同位角相等,两直线平行)
∵ ∠2 +∠3=180°(已知)
∴ AC∥MD(同旁内角互补,两直线平行)
例2 如图,AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由.
典型例题
∵∠1=∠2(已知),
∴EF∥CD(内错角相等,两直线平行).
又∵AB∥CD (已知),
∴ EF∥AB(平行于同一条直线的两条直线平行).
例3 如图,已知直线a∥b,直线c∥d,∠1=107°,求∠2,∠3的度数.
典型例题
∵a∥b (已知),
∴∠2=∠1=107°(两直线平行,内错角相等).
∵ c∥d (已知),
∴∠1+∠3=180°(两直线平行,同旁内角互补),
∴∠3= 180°-∠1=180°-107°=73°.
1.著名的比萨斜塔建成于12世纪,从建成之日起就一直在倾斜. 目前,它与地面所成的较小的角为85°(如图所示),它与地面所成的较大的角是多少度?你的依据是什么?
深化提高
1
2
a
b
∵a∥b(已知),
∴∠1=85°(两直线平行,同位角相等).
∵ ∠1+ ∠2=180° (已知),
∴∠2=180°-∠1=95°.
2.如图,∠A=∠D,如果∠B=20°,那么∠C为( )
A.40°
B.20°
C.60°
D.70°
深化提高
解:∵∠A=∠D(已知),
∴AB∥CD(内错角相等,两直线平行).
∵∠B=20°(已知),
∴∠C=∠B=20°(两直线平行,内错角相等).
B
3.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°, 则∠4的度数是( )
A.35° B.70°
C.90° D.110°
深化提高
D
解:∵∠1=∠2 (已知),
∴a∥b(同位角相等,两直线平行),
∴∠3=∠5 (两直线平行,同位角相等).
∵∠3=70° (已知),
∴∠5=70° (等量代换),
∴∠4=180°-70°=110°(邻补角互补).
例4 一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面 AE,则∠ABC+∠BCD=______°.
典型例题
解:过B作BF∥AE,
∵ CD∥AE, BF∥AE(已知)
∴CD∥BF(平行于同一条直线的两直线平行),
∴∠BCD+∠1=180°(两直线平行,同旁内角互补).
又∵AB⊥AE,∴AB⊥BF,
∴∠ABF =90°,
∴∠ABC+∠BCD=90°+180°=270°.
270
思考:∠ABC+∠BCD+∠BAE=______°.
360
聚焦模型
如图,AB//CD,试解决下列问题:
(1)如图1 ,∠1+∠2=______;
(2)如图2 ,∠1+∠2+∠3=_____;
A
B
C
D
1
2
图1
B
A
E
C
D
1
2
3
图2
180°
360°
测量-猜想-验证
证明:过E作EF∥AB,
∵ AB∥CD,EF∥AB (已知)
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠CEF+∠3=180°(两直线平行,同旁内角互补).
∵ EF∥AB (已知),
∴∠AEF+∠1=180°(两直线平行,同旁内角互补)
∵ ∠CEF+∠AEF=∠2
∴ ∠1+∠2+∠3= 360°.
F
“铅笔模型”
(3)如图3 ,∠1+∠2+∠3+∠4= ;
(4)如图4 ,试探究∠1+∠2+∠3+∠4+…∠n= ;
如图,AB//CD,试解决下列问题:
(1)如图1 ,∠1+∠2=______;
(2)如图2 ,∠1+∠2+∠3=_____;
A
B
C
D
1
2
图1
B
A
E
C
D
1
2
3
图2
180°
360°
聚焦模型
B
A
E
C
D
F
1
2
4
3
图3
2
E
B
A
C
D
N
1
n
图4
540°
180°(n-1)
从特殊到一般
F
如图,如果AB ∥CD,请探索∠A 、∠C、∠E的关系,并说明理由.
聚焦模型
A
B
C
D
E
∠E = ∠A +∠C
F
证明:过E作EF∥AB,
∵ AB∥CD,EF∥AB (已知)
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠CEF=∠C(两直线平行,内错角相等).
∵ EF∥AB (已知),
∴∠AEF= ∠A (两直线平行,内错角相等)
∵ ∠AEC=∠CEF+∠AEF
∴ ∠AEC= ∠A + ∠C.
“猪脚模型”
1.如图,直线 a//b//c,直角三角板的直角顶点落在直线b上.
若∠1=35°,则∠2= .
55°
95°
模型应用
2.如图,AB ∥CD,∠B=120°,∠D=145°,则∠BED = .
课堂小结
条件 结论
判定直线平行
平行线的性质
同位角相等
两直线平行
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
同位角相等
两直线平行 内错角相等
同旁内角互补
条件
性质
条件:角的关系 线的关系
性质:线的关系 角的关系
课堂小结
B
课堂小测
2 . 如图,在三角形ABC中,∠A=∠B.
(1)请你添加一个与直线AB相关的条件,由此可推得CE是∠ACD的平分线(只添加条件,不说理由);
(2)请你添加一个与∠A有关的条件,由此可推得CE是∠ACD的平分线(要写出理由).
课堂小测
解:(1)添加EC∥AB.
(2)添加∠A=∠ACE,则CE是∠ACD的平分线.理由如下:
因为∠A=∠ACE(已知),
所以EC∥AB(内错角相等,两直线平行),
所以∠B=∠DCE(两直线平行,同位角相等).
又因为∠A=∠B(已知),
所以∠ACE=∠DCE(等量代换),
即CE是∠ACD的平分线(角平分线的定义) .
课堂小测
3 . 如图所示,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处),再从学校出发,向北偏西75°的方向走到小明家(图中C处),试问∠ABC为多少度?
解:由题意得:DB∥AE,
所以∠DBA=∠EAB=40°.
又因为∠CBD=75°,
所以∠ABC=∠CBD-∠DBA=75°-40°=35°.
课堂小测
课堂小测
课堂小测
课堂小测
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
旧知回顾
问题1:判别直线平行的条件有哪几个?
你现在一共有几个判定直线平行的方法?
问题2:平行线的性质有哪几条?
问题3:在应用二者时应注意什么问题?
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
旧知回顾
如图1,若a∥b,b∥c,则a∥c.
如图2,若a⊥b,a⊥c,则b∥c.
平行于同一条直线的两条直线平行.
垂直于同一条直线的两条直线平行.
a
b
c
图1
a
b
c
图2
3 平行线的性质
第2课时 平行线的性质与判定的综合运用
学习目标
进一步掌握平行线的性质,能够根据平行线的性质与判定进行简单的推理与计算.
新知探究
1. 平行线的性质的几何符号语言
探究:如图,因为AB∥CD,
所以∠1=____( ).
因为AB∥CD,
所以∠3=____( ).
因为AB∥CD,
所以_________=180°(_____________________________).
∠2
∠2
两直线平行,同位角相等
∠4+∠2
两直线平行,同旁内角互补
两直线平行,内错角相等
新知探究
2. 如图:(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
BF∥CE
内错角相等,两直线平行
BF∥AM
同位角相等,两直线平行
AC∥MD
同旁内角互补,两直线平行
新知探究
【归纳】
由角相等或互补(数量关系)得到两条直线平行(位置关系),
这是平行线的条件;
由两条直线平行(位置关系)得到有关角相等或互补(数量关系),
这是平行线的性质.
【点拨】
平行线的条件与性质是互逆关系,解答题目时一定要区分开!
新知探究
知识点训练:平行线的性质
例:如图,AC∥BD,AE平分∠BAC 交BD于点E.
若∠1=64°,求∠2的度数.
解:由图可知∠1+∠BAC =180°,
由∠1=64°,从而求得∠BAC= 116°,
再由AE平分∠BAC,可得∠CAE =58°,
由AC∥BD,可得∠2+∠CAE =180°,
从而求得∠2=180°-58°=122°.
新知探究
【规律总结】
解决已知两直线平行,求角的关系的问题的基本思路
(1)直接法:找图中的同位角、内错角、同旁内角,进而判断它们的关系 .
(2)间接法:如果没有上述角,通过添加辅助线,构造平行线,得三类角,进而求解 .
例1 根据下图所示,回答下列问题:
(1)若∠1=∠2,可以判定哪两条直线平行?根据是什么?
(2)若∠2=∠M,可以判定哪两条直线平行?根据是什么?
(3)若∠2 +∠3=180°,可以判定哪两条直线平行?根据是什么?
典型例题
∵ ∠1=∠2(已知)
∴ BF∥CE(内错角相等,两直线平行)
∵ ∠2=∠M(已知)
∴ AM∥BF(同位角相等,两直线平行)
∵ ∠2 +∠3=180°(已知)
∴ AC∥MD(同旁内角互补,两直线平行)
例2 如图,AB∥CD,如果∠1=∠2,那么EF与AB平行吗?说说你的理由.
典型例题
∵∠1=∠2(已知),
∴EF∥CD(内错角相等,两直线平行).
又∵AB∥CD (已知),
∴ EF∥AB(平行于同一条直线的两条直线平行).
例3 如图,已知直线a∥b,直线c∥d,∠1=107°,求∠2,∠3的度数.
典型例题
∵a∥b (已知),
∴∠2=∠1=107°(两直线平行,内错角相等).
∵ c∥d (已知),
∴∠1+∠3=180°(两直线平行,同旁内角互补),
∴∠3= 180°-∠1=180°-107°=73°.
1.著名的比萨斜塔建成于12世纪,从建成之日起就一直在倾斜. 目前,它与地面所成的较小的角为85°(如图所示),它与地面所成的较大的角是多少度?你的依据是什么?
深化提高
1
2
a
b
∵a∥b(已知),
∴∠1=85°(两直线平行,同位角相等).
∵ ∠1+ ∠2=180° (已知),
∴∠2=180°-∠1=95°.
2.如图,∠A=∠D,如果∠B=20°,那么∠C为( )
A.40°
B.20°
C.60°
D.70°
深化提高
解:∵∠A=∠D(已知),
∴AB∥CD(内错角相等,两直线平行).
∵∠B=20°(已知),
∴∠C=∠B=20°(两直线平行,内错角相等).
B
3.如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°, 则∠4的度数是( )
A.35° B.70°
C.90° D.110°
深化提高
D
解:∵∠1=∠2 (已知),
∴a∥b(同位角相等,两直线平行),
∴∠3=∠5 (两直线平行,同位角相等).
∵∠3=70° (已知),
∴∠5=70° (等量代换),
∴∠4=180°-70°=110°(邻补角互补).
例4 一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面 AE,则∠ABC+∠BCD=______°.
典型例题
解:过B作BF∥AE,
∵ CD∥AE, BF∥AE(已知)
∴CD∥BF(平行于同一条直线的两直线平行),
∴∠BCD+∠1=180°(两直线平行,同旁内角互补).
又∵AB⊥AE,∴AB⊥BF,
∴∠ABF =90°,
∴∠ABC+∠BCD=90°+180°=270°.
270
思考:∠ABC+∠BCD+∠BAE=______°.
360
聚焦模型
如图,AB//CD,试解决下列问题:
(1)如图1 ,∠1+∠2=______;
(2)如图2 ,∠1+∠2+∠3=_____;
A
B
C
D
1
2
图1
B
A
E
C
D
1
2
3
图2
180°
360°
测量-猜想-验证
证明:过E作EF∥AB,
∵ AB∥CD,EF∥AB (已知)
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠CEF+∠3=180°(两直线平行,同旁内角互补).
∵ EF∥AB (已知),
∴∠AEF+∠1=180°(两直线平行,同旁内角互补)
∵ ∠CEF+∠AEF=∠2
∴ ∠1+∠2+∠3= 360°.
F
“铅笔模型”
(3)如图3 ,∠1+∠2+∠3+∠4= ;
(4)如图4 ,试探究∠1+∠2+∠3+∠4+…∠n= ;
如图,AB//CD,试解决下列问题:
(1)如图1 ,∠1+∠2=______;
(2)如图2 ,∠1+∠2+∠3=_____;
A
B
C
D
1
2
图1
B
A
E
C
D
1
2
3
图2
180°
360°
聚焦模型
B
A
E
C
D
F
1
2
4
3
图3
2
E
B
A
C
D
N
1
n
图4
540°
180°(n-1)
从特殊到一般
F
如图,如果AB ∥CD,请探索∠A 、∠C、∠E的关系,并说明理由.
聚焦模型
A
B
C
D
E
∠E = ∠A +∠C
F
证明:过E作EF∥AB,
∵ AB∥CD,EF∥AB (已知)
∴EF∥CD(平行于同一条直线的两直线平行),
∴∠CEF=∠C(两直线平行,内错角相等).
∵ EF∥AB (已知),
∴∠AEF= ∠A (两直线平行,内错角相等)
∵ ∠AEC=∠CEF+∠AEF
∴ ∠AEC= ∠A + ∠C.
“猪脚模型”
1.如图,直线 a//b//c,直角三角板的直角顶点落在直线b上.
若∠1=35°,则∠2= .
55°
95°
模型应用
2.如图,AB ∥CD,∠B=120°,∠D=145°,则∠BED = .
课堂小结
条件 结论
判定直线平行
平行线的性质
同位角相等
两直线平行
内错角相等
同旁内角互补
两直线平行
同位角相等
内错角相等
同旁内角互补
同位角相等
两直线平行 内错角相等
同旁内角互补
条件
性质
条件:角的关系 线的关系
性质:线的关系 角的关系
课堂小结
B
课堂小测
2 . 如图,在三角形ABC中,∠A=∠B.
(1)请你添加一个与直线AB相关的条件,由此可推得CE是∠ACD的平分线(只添加条件,不说理由);
(2)请你添加一个与∠A有关的条件,由此可推得CE是∠ACD的平分线(要写出理由).
课堂小测
解:(1)添加EC∥AB.
(2)添加∠A=∠ACE,则CE是∠ACD的平分线.理由如下:
因为∠A=∠ACE(已知),
所以EC∥AB(内错角相等,两直线平行),
所以∠B=∠DCE(两直线平行,同位角相等).
又因为∠A=∠B(已知),
所以∠ACE=∠DCE(等量代换),
即CE是∠ACD的平分线(角平分线的定义) .
课堂小测
3 . 如图所示,小张从家(图中A处)出发,向南偏东40°的方向走到学校(图中B处),再从学校出发,向北偏西75°的方向走到小明家(图中C处),试问∠ABC为多少度?
解:由题意得:DB∥AE,
所以∠DBA=∠EAB=40°.
又因为∠CBD=75°,
所以∠ABC=∠CBD-∠DBA=75°-40°=35°.
课堂小测
课堂小测
课堂小测
课堂小测
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
