2.4 用尺规作图 课件(共25张PPT)
文档属性
| 名称 | 2.4 用尺规作图 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
数学史
尺规作图有着悠久的历史. 直尺的功能是:在两点间连接一条线段,将线段向两方向延长.圆规的功能是:以任意一点为圆心,任意长为半径作一个圆;以任意一点为圆心,任意长为半径画一段弧. 利用尺规可以作出许多优美的图案.
数学家高斯幼年时就表现出超人的数学天才.1795年进入格丁根大学学习,第二年他就发现正十七边形的尺规作图法,并给出可用尺规作出的正多边形的条件,解决了欧几里得以来悬而未决的问题.
尺规作图欣赏
尺规作图欣赏
4 用尺规作图
学习目标
1.能用尺规作一个角等于已知角;
2.能利用尺规作角的和、差、倍.
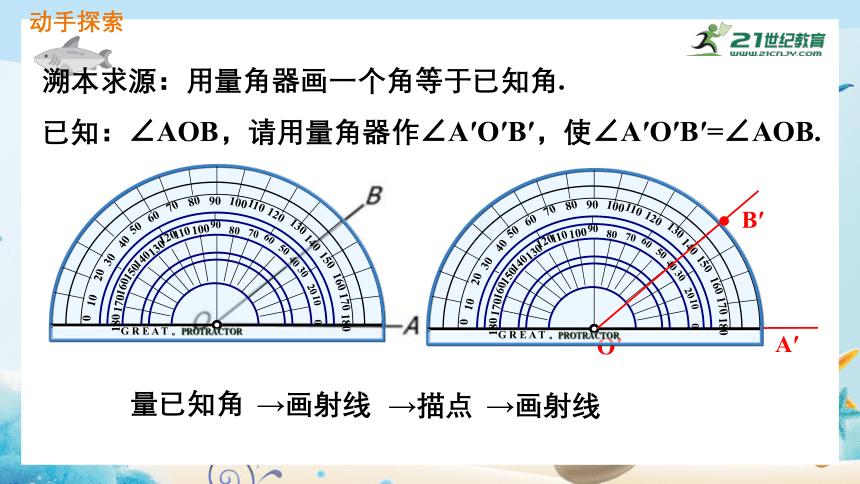
溯本求源:用量角器画一个角等于已知角.
已知:∠AOB,请用量角器作∠A′O′B′,使∠A′O′B′=∠AOB.
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
量已知角
→画射线
O′
A′
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
→描点
B′
→画射线
动手探索
溯本求源:用刻度磨损量角器画一个角等于已知角.
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
O′
A′
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
B′
动手探索
探究新知:用尺规画一个角等于已知角.
已知:∠AOB,请用尺规作∠A′O′B′,使∠A′O′B′=∠AOB.
作法 示范
O′
A′
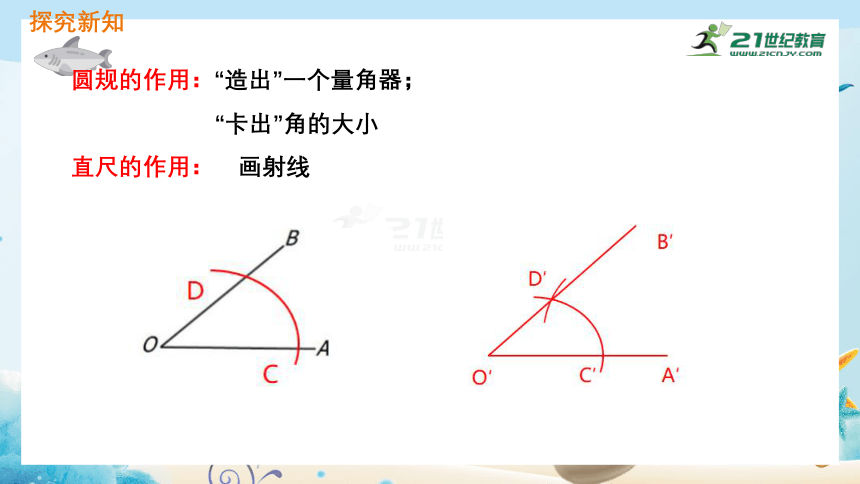
①作射线O′A′;
②以点O为圆心,任意长为半径画弧,交OA于点C,交OB于点D ;
③以点O′为圆心,以同样(OC)长为半径画弧,交O′A′于点 C′ ;
④以点C′为圆心,CD 为半径画弧,交前面的弧于点 D′;
⑤过点 D′ 作射线O′B′.
C
D
C′
D′
B′
“三弧两线”
圆规的作用:“造出”一个量角器;
“卡出”角的大小
直尺的作用: 画射线
探究新知
尺规作图的判断:
下列作图属于尺规作图的是( )
A.画线段MN=3cm
B.用量角器画出∠AOB的平分线
C.用三角尺作过点A垂直于直线l的直线
D.已知∠α ,用没有刻度的直尺和圆规作∠AOB ,使∠AOB=2∠α
探究新知
D
利用尺规,作一个角等于已知角.
已知:∠AOB(如图).
求作:∠A′O′B′=∠AOB.
B
O
A
探究新知
(1)作射线O′A′;
作法:
(2)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,同样长为半径画弧,交O′A′于点C′;
(4)以点C’为圆心,CD长为半径作弧,交前面的弧于点D’ ;
(5)过点D′作射线O′B′ .∠A′O′B′就是所求的角.
O
D'
C'
B
A
C
D
B'
O'
A'
O
D'
C'
B
A
C
D
B'
O'
A'
作一个角等于已知角可以归纳为“一线三弧”:
先画一条射线,再作三次弧.
其中前两次弧半径相同,
而第三次以原角的两边与弧的交点之间的距离为半径.
典型例题
例1 已知:∠AOB.
利用尺规作:∠A’O’B’,使∠A’O’B’=2∠AOB.
B
O
A
作法一:
A’
∠A’OB’即为所求作的角.
C
B’
B
O
A
作法二:
C
D
E
B’
O’
A’
C’
例2 如图,已知∠A,∠B,求作一个角,使它等于
∠A-∠B(不用写作法,保留作图痕迹).
典型例题
A
B
提示:作∠COD=∠A,并在∠COD的内部作∠DOE=∠B,则∠COE就是所求作的角.
A
B
C
O
D
典型例题
作∠COD=∠A,并在∠COD的内部作∠DOE=∠B,则∠COE就是所求作的角.
E
变式:如图,已知∠A,∠B,求作一个角,使它等于∠A+∠B
(不用写作法,保留作图痕迹).
A
B
作已知角的和、差、倍角:
1.作两个已知角的和,是在一个已知角的外部作一个角等于已知角等于另一个已知角;
2.作两个已知角的差,是在一个已知角的内部作一个角等于另一个已知角;
3.做一个已知角的n倍,可以看成作n个已知角的和.
A
B
C
O
D
E
作已知角的和、差、倍角:
1.作两个已知角的和,是在一个已知角的外部作一个角等于已知角等于另一个已知角;
2.作两个已知角的差,是在一个已知角的内部作一个角等于另一个已知角;
3.做一个已知角的n倍,可以看成作n个已知角的和.
作一个角等于已知角可以归纳为“一线三弧”:
先画一条射线,再作三次弧.
其中前两次弧半径相同,
而第三次以原角的两边与弧的交点之间的距离为半径.
课堂小结
做一做学案中的随堂检测试题.
随堂检测
或优教平台“同步课堂”-“课堂教学”栏目下,本课时授课包“互动课堂”训练.
1. 通过本节课的学习,你学到了哪些知识?
2. 掌握了哪些学习方法?
3. 关于尺规作图,你还有想要继续探讨的问题吗?
课堂小结
1.画一个钝角∠AOB,然后以O为顶点,以OA为一边,在角的内部画一条射线OC,使∠AOC=90°,正确的图形是( )
2.如图所示,过点P作直线a的平行线b的作法依据( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
D
D
当堂检测
3.已知∠AOB,请用尺规作∠A'O'B',使∠A'O'B'=2∠AOB.
O′
A′
C
D
C′
B′
E
∠ A'O'B'即为所求作的角
当堂检测
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
数学史
尺规作图有着悠久的历史. 直尺的功能是:在两点间连接一条线段,将线段向两方向延长.圆规的功能是:以任意一点为圆心,任意长为半径作一个圆;以任意一点为圆心,任意长为半径画一段弧. 利用尺规可以作出许多优美的图案.
数学家高斯幼年时就表现出超人的数学天才.1795年进入格丁根大学学习,第二年他就发现正十七边形的尺规作图法,并给出可用尺规作出的正多边形的条件,解决了欧几里得以来悬而未决的问题.
尺规作图欣赏
尺规作图欣赏
4 用尺规作图
学习目标
1.能用尺规作一个角等于已知角;
2.能利用尺规作角的和、差、倍.
溯本求源:用量角器画一个角等于已知角.
已知:∠AOB,请用量角器作∠A′O′B′,使∠A′O′B′=∠AOB.
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
量已知角
→画射线
O′
A′
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
→描点
B′
→画射线
动手探索
溯本求源:用刻度磨损量角器画一个角等于已知角.
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
O′
A′
90
120
150
180
60
30
G R E A T 。PROTRACTOR
0
0
10
20
50
40
30
60
70
80
90
100
110
120
130
140
150
160
170
180
10
20
40
50
70
80
100
110
130
140
160
170
B′
动手探索
探究新知:用尺规画一个角等于已知角.
已知:∠AOB,请用尺规作∠A′O′B′,使∠A′O′B′=∠AOB.
作法 示范
O′
A′
①作射线O′A′;
②以点O为圆心,任意长为半径画弧,交OA于点C,交OB于点D ;
③以点O′为圆心,以同样(OC)长为半径画弧,交O′A′于点 C′ ;
④以点C′为圆心,CD 为半径画弧,交前面的弧于点 D′;
⑤过点 D′ 作射线O′B′.
C
D
C′
D′
B′
“三弧两线”
圆规的作用:“造出”一个量角器;
“卡出”角的大小
直尺的作用: 画射线
探究新知
尺规作图的判断:
下列作图属于尺规作图的是( )
A.画线段MN=3cm
B.用量角器画出∠AOB的平分线
C.用三角尺作过点A垂直于直线l的直线
D.已知∠α ,用没有刻度的直尺和圆规作∠AOB ,使∠AOB=2∠α
探究新知
D
利用尺规,作一个角等于已知角.
已知:∠AOB(如图).
求作:∠A′O′B′=∠AOB.
B
O
A
探究新知
(1)作射线O′A′;
作法:
(2)以点O为圆心,以任意长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,同样长为半径画弧,交O′A′于点C′;
(4)以点C’为圆心,CD长为半径作弧,交前面的弧于点D’ ;
(5)过点D′作射线O′B′ .∠A′O′B′就是所求的角.
O
D'
C'
B
A
C
D
B'
O'
A'
O
D'
C'
B
A
C
D
B'
O'
A'
作一个角等于已知角可以归纳为“一线三弧”:
先画一条射线,再作三次弧.
其中前两次弧半径相同,
而第三次以原角的两边与弧的交点之间的距离为半径.
典型例题
例1 已知:∠AOB.
利用尺规作:∠A’O’B’,使∠A’O’B’=2∠AOB.
B
O
A
作法一:
A’
∠A’OB’即为所求作的角.
C
B’
B
O
A
作法二:
C
D
E
B’
O’
A’
C’
例2 如图,已知∠A,∠B,求作一个角,使它等于
∠A-∠B(不用写作法,保留作图痕迹).
典型例题
A
B
提示:作∠COD=∠A,并在∠COD的内部作∠DOE=∠B,则∠COE就是所求作的角.
A
B
C
O
D
典型例题
作∠COD=∠A,并在∠COD的内部作∠DOE=∠B,则∠COE就是所求作的角.
E
变式:如图,已知∠A,∠B,求作一个角,使它等于∠A+∠B
(不用写作法,保留作图痕迹).
A
B
作已知角的和、差、倍角:
1.作两个已知角的和,是在一个已知角的外部作一个角等于已知角等于另一个已知角;
2.作两个已知角的差,是在一个已知角的内部作一个角等于另一个已知角;
3.做一个已知角的n倍,可以看成作n个已知角的和.
A
B
C
O
D
E
作已知角的和、差、倍角:
1.作两个已知角的和,是在一个已知角的外部作一个角等于已知角等于另一个已知角;
2.作两个已知角的差,是在一个已知角的内部作一个角等于另一个已知角;
3.做一个已知角的n倍,可以看成作n个已知角的和.
作一个角等于已知角可以归纳为“一线三弧”:
先画一条射线,再作三次弧.
其中前两次弧半径相同,
而第三次以原角的两边与弧的交点之间的距离为半径.
课堂小结
做一做学案中的随堂检测试题.
随堂检测
或优教平台“同步课堂”-“课堂教学”栏目下,本课时授课包“互动课堂”训练.
1. 通过本节课的学习,你学到了哪些知识?
2. 掌握了哪些学习方法?
3. 关于尺规作图,你还有想要继续探讨的问题吗?
课堂小结
1.画一个钝角∠AOB,然后以O为顶点,以OA为一边,在角的内部画一条射线OC,使∠AOC=90°,正确的图形是( )
2.如图所示,过点P作直线a的平行线b的作法依据( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
D
D
当堂检测
3.已知∠AOB,请用尺规作∠A'O'B',使∠A'O'B'=2∠AOB.
O′
A′
C
D
C′
B′
E
∠ A'O'B'即为所求作的角
当堂检测
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
