华师大版数学七年级下册同步:9.1.2 三角形的内角和与外角和 课件(共21张PPT)
文档属性
| 名称 | 华师大版数学七年级下册同步:9.1.2 三角形的内角和与外角和 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 161.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 21:14:49 | ||
图片预览



文档简介
(共21张PPT)
第9章 多边形
9.1.2 三角形的内角和与外角和
课程导入
1.量一量:一副三角板的每个角各是多少度?一个三角板三个内角的和各是多少?
2.猜一猜:任意一个三角形的三个内角和都相同吗?它是多少度呢?
3.动动手,仔细观察:
(1)拼拼看,将任意一个三角形的三个内角拼合在一起会形成什么角?
(2)观察:小组内观察比较,会得出什么结论?
获取新知
做一做
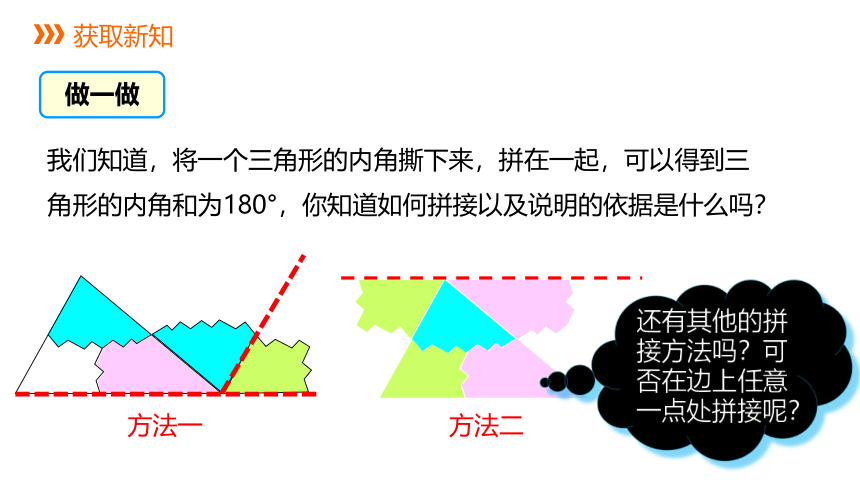
我们知道,将一个三角形的内角撕下来,拼在一起,可以得到三角形的内角和为180°,你知道如何拼接以及说明的依据是什么吗?
还有其他的拼接方法吗?可否在边上任意一点处拼接呢?
方法一
方法二
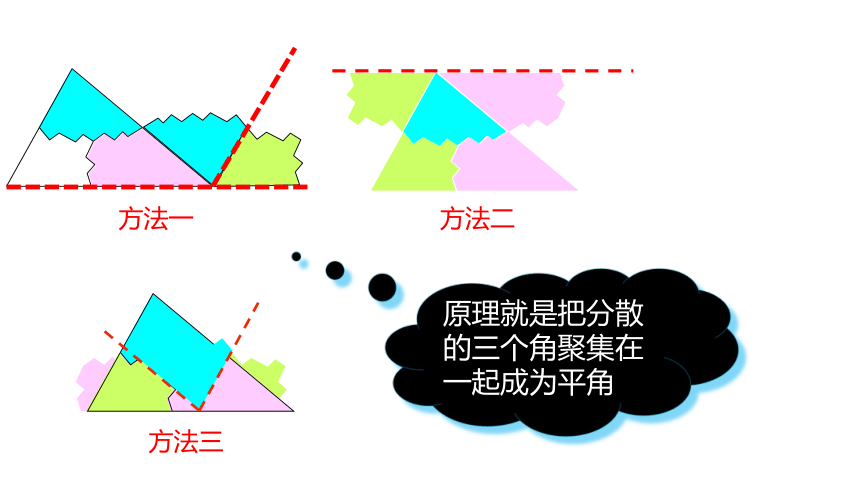
方法三
方法一
方法二
原理就是把分散的三个角聚集在一起成为平角
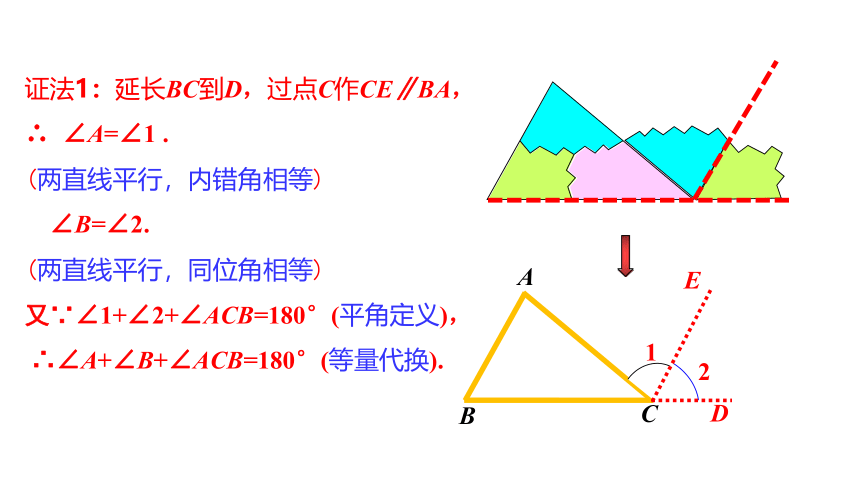
证法1:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°(平角定义),
∴∠A+∠B+∠ACB=180°(等量代换).
C
B
A
E
D
1
2
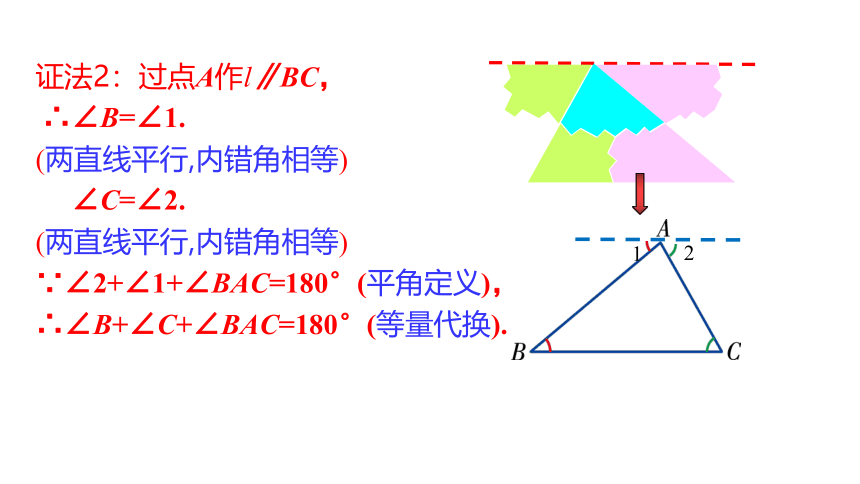
证法2:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°(平角定义),
∴∠B+∠C+∠BAC=180°(等量代换).
1
2
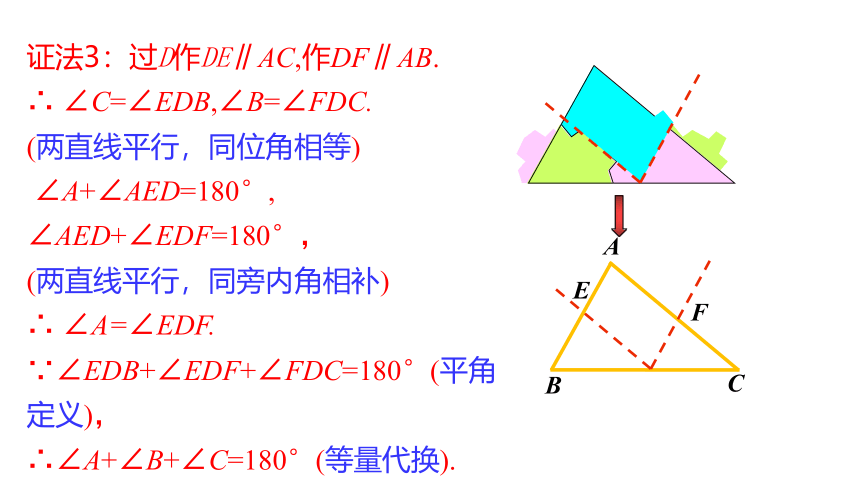
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°(平角定义),
∴∠A+∠B+∠C=180°(等量代换).
C
B
A
E
F
定理:三角形的内角和等于180°.
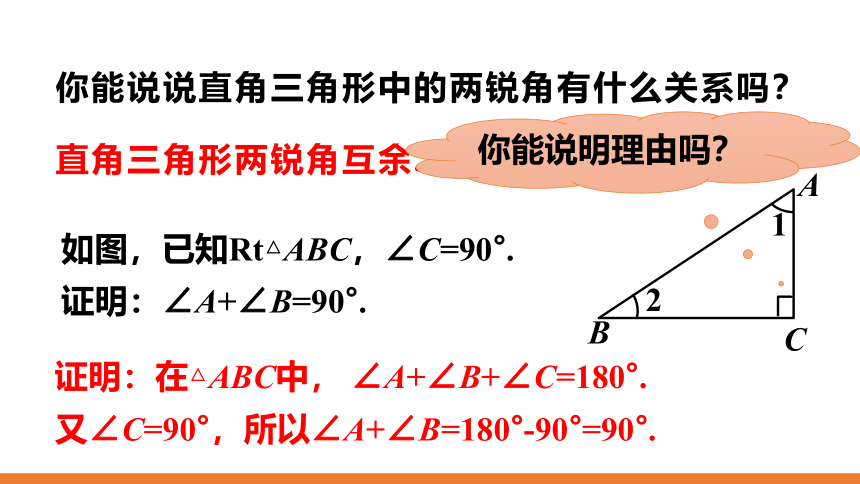
你能说说直角三角形中的两锐角有什么关系吗?
直角三角形两锐角互余.
你能说明理由吗?
如图,已知Rt△ABC,∠C=90°.
证明:∠A+∠B=90°.
证明:在△ABC中, ∠A+∠B+∠C=180°.
又∠C=90°,所以∠A+∠B=180°-90°=90°.
B
A
C
1
2
如图∠A+∠C+∠ABC=180°,∠CBD+∠ABC=180°,从上面两个结论中,你能得出什么结论?
∠CBD=∠A+∠C.
大家通过测量∠A、∠C、∠CBD
的大小来验证结果是否正确.
思考:怎样用文字来表述这个结论?
三角形的一个外角等于与它不相邻的两个内角的和.
A
C
B
D
探索新知:外角性质
问题:∠CBD与∠A、∠C的大小
能确定吗?为什么与∠CBA的大小不
能确定呢?
∠CBD>∠A,∠CBD> ∠C.
∠CBD与∠CBA的大小视情况而定.
思考:怎样用文字来表述这个结论?
三角形的一个外角大于任何一个与它不相邻的内角.
A
C
B
D
探索新知:外角性质
探索新知:外角和
三角形外角和的概念:
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
如图中的 ∠1+∠2+∠3就是△ABC的外角和.
B
A
C
1
2
3
探索新知:外角和
动手实践探索:
在一张白纸上仿下图画出一个图形,然后把 ∠1,∠2,∠3剪下来拼一拼,观察∠1+∠2+∠3的值是多少?
B
A
C
1
2
3
∠1+∠2+∠3=360°
证明:
因为∠1+∠BAC=180°,
∠2+∠ABC =180°,
∠3+∠ACB=180°,
所以∠1+∠BAC+∠2+∠ABC+∠3+∠ACB
=180°×3=540°.
又因为∠BAC+∠ABC+∠ACB=180°,
所以∠1+∠2+∠3=360°.
B
A
C
1
2
3
∠1+∠2+∠3=360°
例题讲解
例1 如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
解:(1)∵∠ADC是△ABD的外角,
∴∠B+∠BAD= ∠ADC=80°.
又∵ ∠B=∠BAD,
∴∠B=80°× =40°.
解:(2)∵∠B+∠BAC+∠C=180°,
∴ ∠C=180°-∠B - ∠BAC
=180°- 40°- 70°
=70°.
随堂演练
1.如图,求∠1,∠2,∠3的度数.
2
155°
3
37°
1
∠1=25°
∠2=62°
∠3=118°
2. 一副三角尺如图摆放(直角顶点C重合),边AB与CE交于点F,
DE//BC,则∠BFC的度数为( )
A.105° B.100° C.75° D.60°
A
3. 在△ABC中,若一个内角等于另外两个内角的差,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
B
4. 如图,以CD为公共边的三角形是_______________;
∠EFB是________的内角;在△BCE中,BE所对
的角是________,∠CBE所对的边是__________;
以∠A为公共角的三角形_______________________.
△ABD,△ACE和△ABC
△CDF与△BCD
△BEF
∠BCE
CE
课堂小结
2、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
3、三角形的外角和是360°
1、三角形内角和是180°
第9章 多边形
9.1.2 三角形的内角和与外角和
课程导入
1.量一量:一副三角板的每个角各是多少度?一个三角板三个内角的和各是多少?
2.猜一猜:任意一个三角形的三个内角和都相同吗?它是多少度呢?
3.动动手,仔细观察:
(1)拼拼看,将任意一个三角形的三个内角拼合在一起会形成什么角?
(2)观察:小组内观察比较,会得出什么结论?
获取新知
做一做
我们知道,将一个三角形的内角撕下来,拼在一起,可以得到三角形的内角和为180°,你知道如何拼接以及说明的依据是什么吗?
还有其他的拼接方法吗?可否在边上任意一点处拼接呢?
方法一
方法二
方法三
方法一
方法二
原理就是把分散的三个角聚集在一起成为平角
证法1:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°(平角定义),
∴∠A+∠B+∠ACB=180°(等量代换).
C
B
A
E
D
1
2
证法2:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°(平角定义),
∴∠B+∠C+∠BAC=180°(等量代换).
1
2
证法3:过D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°(平角定义),
∴∠A+∠B+∠C=180°(等量代换).
C
B
A
E
F
定理:三角形的内角和等于180°.
你能说说直角三角形中的两锐角有什么关系吗?
直角三角形两锐角互余.
你能说明理由吗?
如图,已知Rt△ABC,∠C=90°.
证明:∠A+∠B=90°.
证明:在△ABC中, ∠A+∠B+∠C=180°.
又∠C=90°,所以∠A+∠B=180°-90°=90°.
B
A
C
1
2
如图∠A+∠C+∠ABC=180°,∠CBD+∠ABC=180°,从上面两个结论中,你能得出什么结论?
∠CBD=∠A+∠C.
大家通过测量∠A、∠C、∠CBD
的大小来验证结果是否正确.
思考:怎样用文字来表述这个结论?
三角形的一个外角等于与它不相邻的两个内角的和.
A
C
B
D
探索新知:外角性质
问题:∠CBD与∠A、∠C的大小
能确定吗?为什么与∠CBA的大小不
能确定呢?
∠CBD>∠A,∠CBD> ∠C.
∠CBD与∠CBA的大小视情况而定.
思考:怎样用文字来表述这个结论?
三角形的一个外角大于任何一个与它不相邻的内角.
A
C
B
D
探索新知:外角性质
探索新知:外角和
三角形外角和的概念:
与三角形的每个内角相邻的外角分别有两个,这两个外角是对顶角,从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
如图中的 ∠1+∠2+∠3就是△ABC的外角和.
B
A
C
1
2
3
探索新知:外角和
动手实践探索:
在一张白纸上仿下图画出一个图形,然后把 ∠1,∠2,∠3剪下来拼一拼,观察∠1+∠2+∠3的值是多少?
B
A
C
1
2
3
∠1+∠2+∠3=360°
证明:
因为∠1+∠BAC=180°,
∠2+∠ABC =180°,
∠3+∠ACB=180°,
所以∠1+∠BAC+∠2+∠ABC+∠3+∠ACB
=180°×3=540°.
又因为∠BAC+∠ABC+∠ACB=180°,
所以∠1+∠2+∠3=360°.
B
A
C
1
2
3
∠1+∠2+∠3=360°
例题讲解
例1 如图,D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B的度数;
(2)∠C的度数.
A
B
C
D
解:(1)∵∠ADC是△ABD的外角,
∴∠B+∠BAD= ∠ADC=80°.
又∵ ∠B=∠BAD,
∴∠B=80°× =40°.
解:(2)∵∠B+∠BAC+∠C=180°,
∴ ∠C=180°-∠B - ∠BAC
=180°- 40°- 70°
=70°.
随堂演练
1.如图,求∠1,∠2,∠3的度数.
2
155°
3
37°
1
∠1=25°
∠2=62°
∠3=118°
2. 一副三角尺如图摆放(直角顶点C重合),边AB与CE交于点F,
DE//BC,则∠BFC的度数为( )
A.105° B.100° C.75° D.60°
A
3. 在△ABC中,若一个内角等于另外两个内角的差,则这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
B
4. 如图,以CD为公共边的三角形是_______________;
∠EFB是________的内角;在△BCE中,BE所对
的角是________,∠CBE所对的边是__________;
以∠A为公共角的三角形_______________________.
△ABD,△ACE和△ABC
△CDF与△BCD
△BEF
∠BCE
CE
课堂小结
2、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
3、三角形的外角和是360°
1、三角形内角和是180°
