华师大版数学七年级下册同步课件:9.3 用正多边形铺设地面(共32张PPT)
文档属性
| 名称 | 华师大版数学七年级下册同步课件:9.3 用正多边形铺设地面(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 764.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-18 21:10:49 | ||
图片预览




文档简介
(共32张PPT)
第9章 多边形
9.3 用正多边形铺设地面
情景导入
这些形状的地砖可以铺满整个地面不留空隙
它们的形状都是正多边形,你有什么想法?
使用给定的某种正多边形,它能否铺满地面,既不留下意思空白,又不相互重叠呢?
获取新知
探究
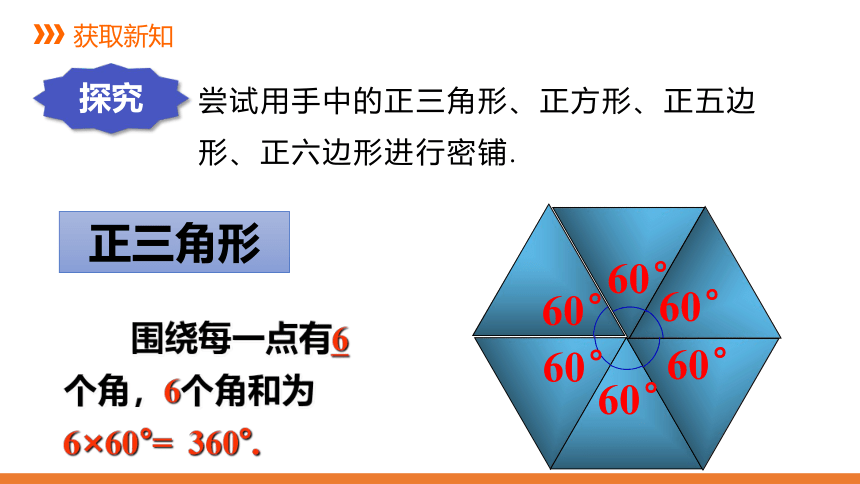
尝试用手中的正三角形、正方形、正五边形、正六边形进行密铺.
60°
60°
60°
60°
60°
60°
正三角形
围绕每一点有6个角,6个角和为6×60°= 360°.
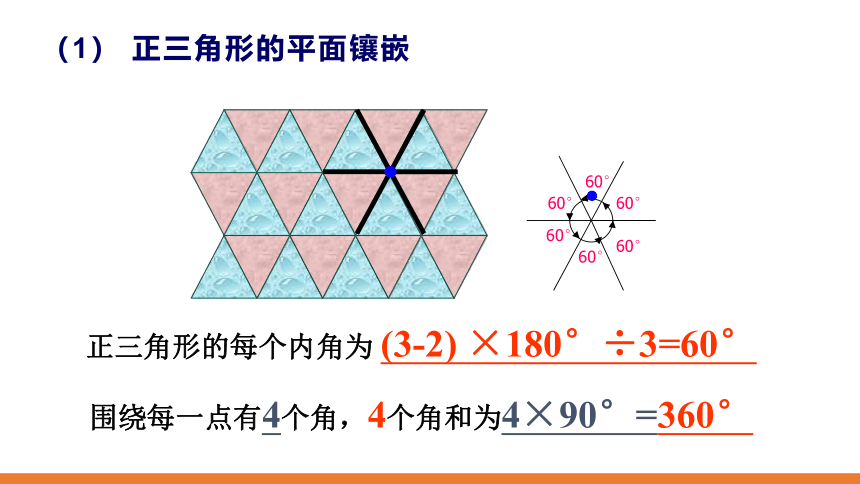
(1) 正三角形的平面镶嵌
60°
60°
60°
60°
60°
60°
正三角形的每个内角为 (3-2) ×180°÷3=60°
围绕每一点有4个角,4个角和为4×90°=360°
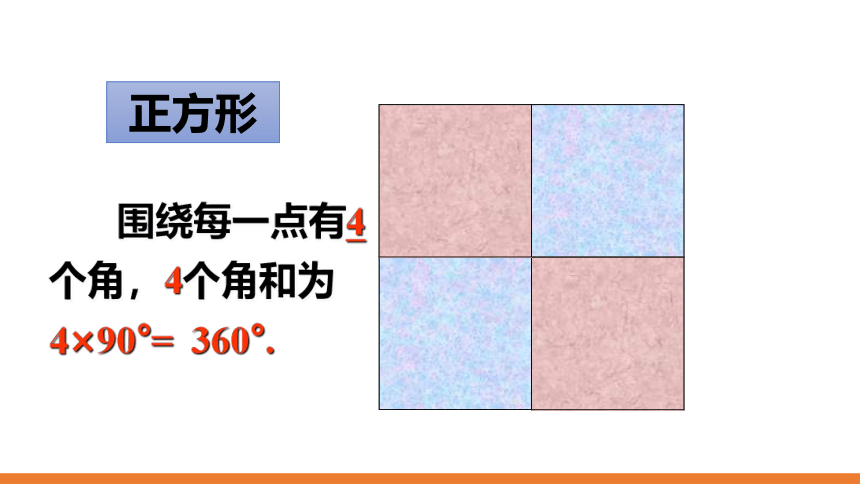
正方形
围绕每一点有4个角,4个角和为4×90°= 360°.
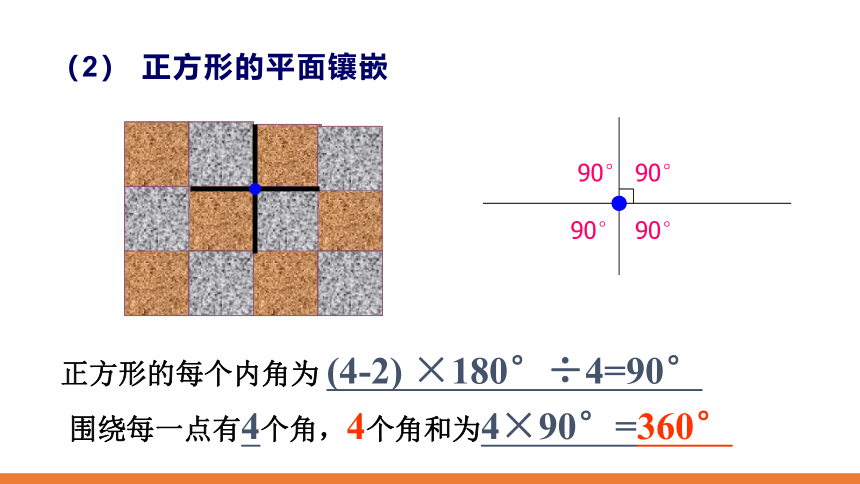
(2) 正方形的平面镶嵌
正方形的每个内角为 (4-2) ×180°÷4=90°
围绕每一点有4个角,4个角和为4×90°=360°
90°
90°
90°
90°
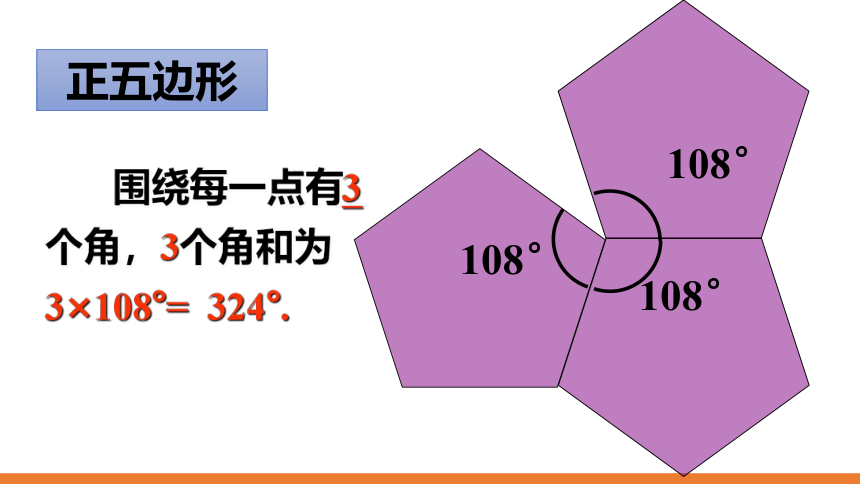
108°
108°
108°
正五边形
围绕每一点有3个角,3个角和为3×108°= 324°.
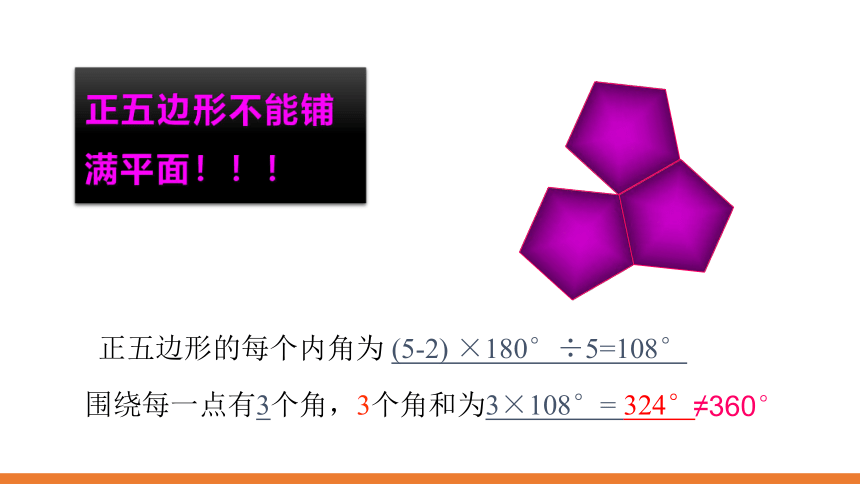
正五边形不能铺满平面!!!
正五边形的每个内角为 (5-2) ×180°÷5=108°
围绕每一点有3个角,3个角和为3×108°= 324°
≠360°
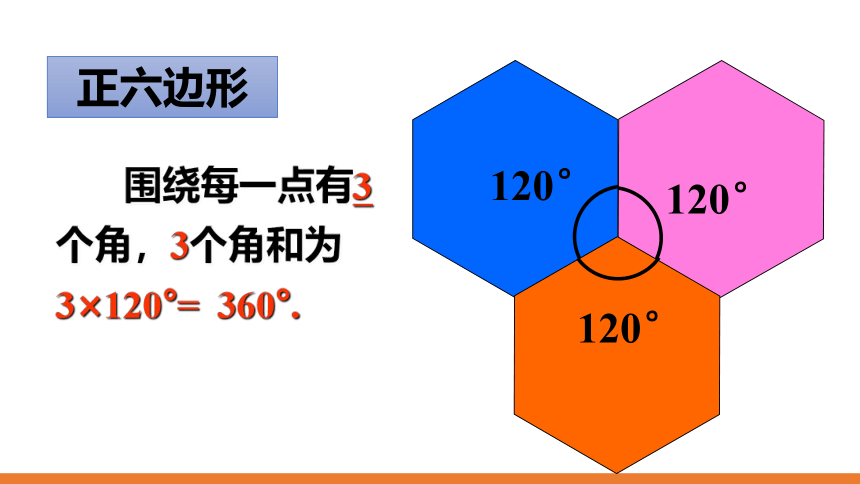
正六边形
120°
120°
120°
围绕每一点有3个角,3个角和为3×120°= 360°.
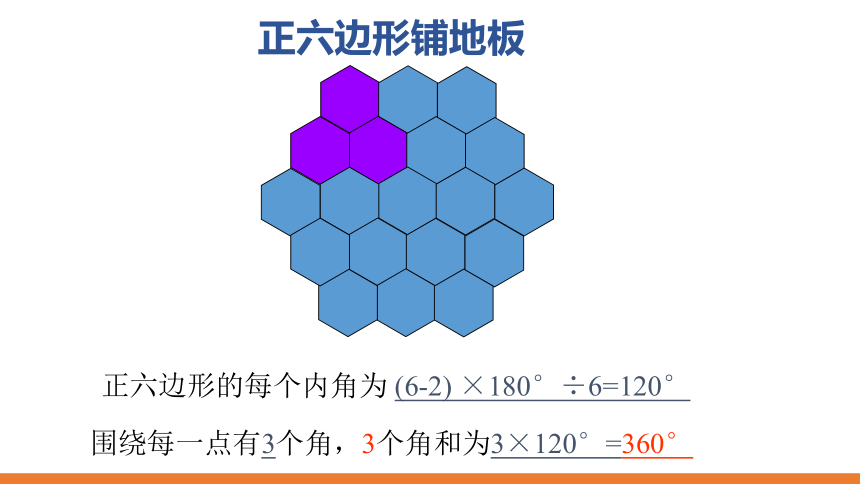
正六边形铺地板
正六边形的每个内角为 (6-2) ×180°÷6=120°
围绕每一点有3个角,3个角和为3×120°=360°
正七八边形呢?
不能!
也不能!
>360°
>360°
正八边形的每个内角为 (8-2) ×180°÷8=135°
围绕每一点有3个角,3个角和为3×135°=405°
正七边形的每个内角为 (7-2) ×180°÷7=128.6°
围绕每一点有3个角,3个角和为3×128.6°=385.8°
?
用一种正多边形铺地板时只能有正三角形、正方形和正六边形三种.
概 括
当围绕一点拼在一起的几个多边形的内角加在一起组成一个周角,即几个角的和为360°时,就可拼成一个既不留空白,又不相互重叠的平面图。
观察上述实验结果,分组讨论:你发现了什么?平面镶嵌的条件是什么?
发现:拼接在同一点的各个角的和恰好等于 360°.
多边形平面镶嵌的条件:
(1)拼接在同一点的各个角的和恰好等于 360°;
(2)相邻的多边形有公共边.
如果是多种正多边形呢?你能铺吗?
正八边形和正方形
正十二边形和正三角形
正三角形和正六边形组合.
正三角形和正方形组合.
正三角形和正十二边形组合.
正方形和正八边形组合.
正十二边形、正方形和正六边形组合.
正三角形、正四边形和正六边形组合.
【归纳总结】 用一种正多边形能铺满地面的条件:
(1)若正多边形的内角度数的整数倍等于360°,则用这种正多边形就可以铺满地面;否则,就不能铺满地面.
(2)只有正三角形、正方形、正六边形这三种正多边形可以单独铺满地面.
随堂演练
1.用一种正多边形能进行平面铺设的条件是 ( )
A.内角都是整数度数 B.边数是3的整数倍
C.内角整除180° D.内角整除360°
D
2.某装修店里出售下列形状的地砖:(1)正三角形;(2)正方形;(3)正六边形;(4)正八边形.若只选购一种地砖来铺满地面,则购买方案共有 ( )
A.1种 B.2种 C.3种 D.4种
C
3.用m个正方形和n个正八边形围绕一个顶点拼成360°,则m,n满足的关系式是 ( )
A.2m+3n=8 B.3m+2n=8 C.m+n=4 D.m+2n=6
A
4.一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三角形、正方形、正六边形,那么另外一个是 ( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
B
知识点一 用一种正多边形铺满地面
用一种正多边形能铺满地面的条件:围绕一点拼在一起的几个内角加在一起恰好能组成一个____________.
如果某种正多边形的内角度数的________是360°,那么用这种正多边形就能铺满地面.
用同一种正多边形能铺满地面的有________、________和________.
周角
整数倍
正三角形
正方形
正六边形
课堂小结
知识点二 用几种不同的正多边形铺满地面
用两种不同的正多边形铺满地面的条件:
(1)每一个拼接点处的所有角之和恰好等于________(围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角);
(2)两种正多边形的边长______.
360°
相等
[点拨] 用两种正多边形能铺满地面的组合有:
(1)正三角形和正方形;
(2)正三角形和正六边形;
(3)正方形和正八边形等.
第9章 多边形
9.3 用正多边形铺设地面
情景导入
这些形状的地砖可以铺满整个地面不留空隙
它们的形状都是正多边形,你有什么想法?
使用给定的某种正多边形,它能否铺满地面,既不留下意思空白,又不相互重叠呢?
获取新知
探究
尝试用手中的正三角形、正方形、正五边形、正六边形进行密铺.
60°
60°
60°
60°
60°
60°
正三角形
围绕每一点有6个角,6个角和为6×60°= 360°.
(1) 正三角形的平面镶嵌
60°
60°
60°
60°
60°
60°
正三角形的每个内角为 (3-2) ×180°÷3=60°
围绕每一点有4个角,4个角和为4×90°=360°
正方形
围绕每一点有4个角,4个角和为4×90°= 360°.
(2) 正方形的平面镶嵌
正方形的每个内角为 (4-2) ×180°÷4=90°
围绕每一点有4个角,4个角和为4×90°=360°
90°
90°
90°
90°
108°
108°
108°
正五边形
围绕每一点有3个角,3个角和为3×108°= 324°.
正五边形不能铺满平面!!!
正五边形的每个内角为 (5-2) ×180°÷5=108°
围绕每一点有3个角,3个角和为3×108°= 324°
≠360°
正六边形
120°
120°
120°
围绕每一点有3个角,3个角和为3×120°= 360°.
正六边形铺地板
正六边形的每个内角为 (6-2) ×180°÷6=120°
围绕每一点有3个角,3个角和为3×120°=360°
正七八边形呢?
不能!
也不能!
>360°
>360°
正八边形的每个内角为 (8-2) ×180°÷8=135°
围绕每一点有3个角,3个角和为3×135°=405°
正七边形的每个内角为 (7-2) ×180°÷7=128.6°
围绕每一点有3个角,3个角和为3×128.6°=385.8°
?
用一种正多边形铺地板时只能有正三角形、正方形和正六边形三种.
概 括
当围绕一点拼在一起的几个多边形的内角加在一起组成一个周角,即几个角的和为360°时,就可拼成一个既不留空白,又不相互重叠的平面图。
观察上述实验结果,分组讨论:你发现了什么?平面镶嵌的条件是什么?
发现:拼接在同一点的各个角的和恰好等于 360°.
多边形平面镶嵌的条件:
(1)拼接在同一点的各个角的和恰好等于 360°;
(2)相邻的多边形有公共边.
如果是多种正多边形呢?你能铺吗?
正八边形和正方形
正十二边形和正三角形
正三角形和正六边形组合.
正三角形和正方形组合.
正三角形和正十二边形组合.
正方形和正八边形组合.
正十二边形、正方形和正六边形组合.
正三角形、正四边形和正六边形组合.
【归纳总结】 用一种正多边形能铺满地面的条件:
(1)若正多边形的内角度数的整数倍等于360°,则用这种正多边形就可以铺满地面;否则,就不能铺满地面.
(2)只有正三角形、正方形、正六边形这三种正多边形可以单独铺满地面.
随堂演练
1.用一种正多边形能进行平面铺设的条件是 ( )
A.内角都是整数度数 B.边数是3的整数倍
C.内角整除180° D.内角整除360°
D
2.某装修店里出售下列形状的地砖:(1)正三角形;(2)正方形;(3)正六边形;(4)正八边形.若只选购一种地砖来铺满地面,则购买方案共有 ( )
A.1种 B.2种 C.3种 D.4种
C
3.用m个正方形和n个正八边形围绕一个顶点拼成360°,则m,n满足的关系式是 ( )
A.2m+3n=8 B.3m+2n=8 C.m+n=4 D.m+2n=6
A
4.一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三角形、正方形、正六边形,那么另外一个是 ( )
A.正三角形 B.正方形
C.正五边形 D.正六边形
B
知识点一 用一种正多边形铺满地面
用一种正多边形能铺满地面的条件:围绕一点拼在一起的几个内角加在一起恰好能组成一个____________.
如果某种正多边形的内角度数的________是360°,那么用这种正多边形就能铺满地面.
用同一种正多边形能铺满地面的有________、________和________.
周角
整数倍
正三角形
正方形
正六边形
课堂小结
知识点二 用几种不同的正多边形铺满地面
用两种不同的正多边形铺满地面的条件:
(1)每一个拼接点处的所有角之和恰好等于________(围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角);
(2)两种正多边形的边长______.
360°
相等
[点拨] 用两种正多边形能铺满地面的组合有:
(1)正三角形和正方形;
(2)正三角形和正六边形;
(3)正方形和正八边形等.
