北师大版七年级数学下册《4.1.4 三角形的高线》课件(共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册《4.1.4 三角形的高线》课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 09:22:35 | ||
图片预览







文档简介
(共23张PPT)
在三角形中,连接一个顶点与它对边中点的线段。
3.三角形的三条中线__________
2.填一填
∵BE是中线,∴_____=_____=
∵CF是中线,∴AB=2____=2____
AE
CE
AC
1
2
1.三角形的中线:
AF
BF
交于一点
5.填一填
∵BE是△ABC的角平分线,∠ABE=______
∵CF是△ABC的角平分线,∴∠ACB=2______=2______
∠CBE
∠ACF
∠BCF
4.三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
1 认识三角形
第4课时 三角形的高线
1.理解三角形高的相关概念,会在具体的三角形中画高,尤其是钝角三角形的高.
2.经历探索三角形三条高之间位置关系的过程.
3.体会类比、猜想、实验、归纳等数学思维方法.
学习目标
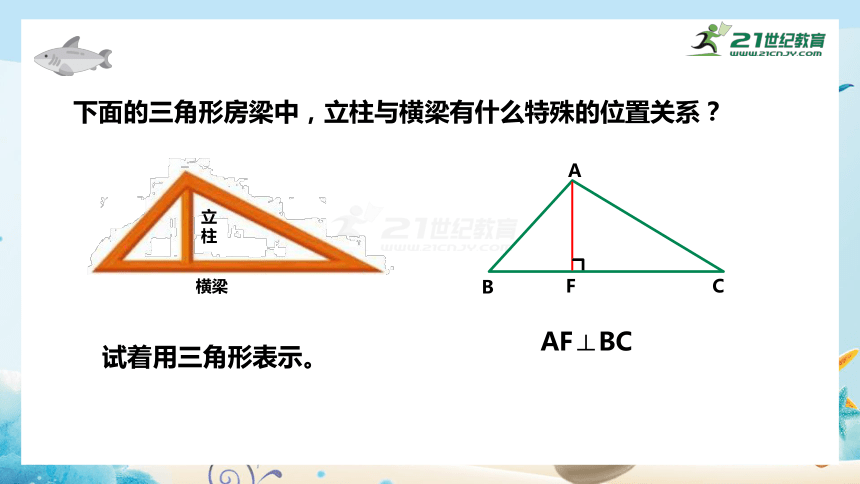
下面的三角形房梁中,立柱与横梁有什么特殊的位置关系?
立
柱
横梁
试着用三角形表示。
A
B
C
F
AF⊥BC
A
B
C
F
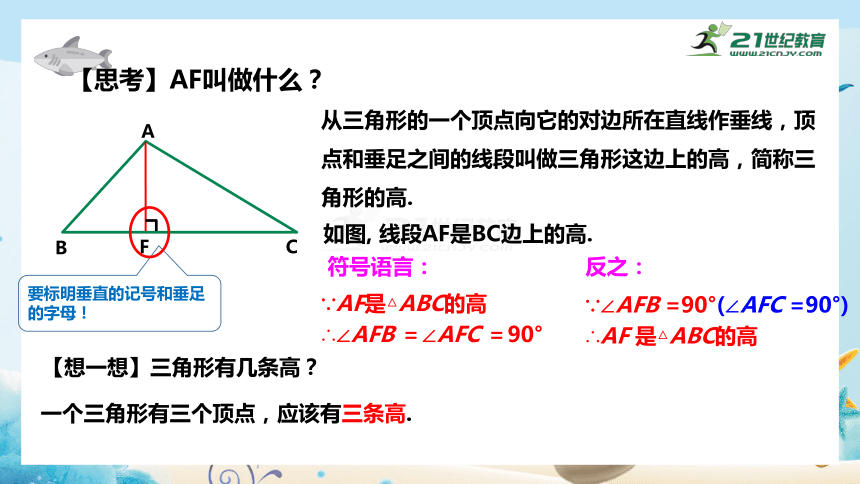
【思考】AF叫做什么?
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
如图, 线段AF是BC边上的高.
【想一想】三角形有几条高?
一个三角形有三个顶点,应该有三条高.
∵AF是△ABC的高
∴∠AFB =∠AFC =90°
符号语言:
反之:
∵∠AFB =90°(∠AFC =90°)
∴AF 是△ABC的高
要标明垂直的记号和垂足的字母!
做一做
每人准备一个锐角三角形纸片。
(1) 你能画出这个三角形的三条高吗
(2) 你能用折纸的办法得到它们吗
使折痕过顶点,顶点的对边边缘重合
(3) 这三条高之间有怎样的位置关系?
锐角三角形的三条高交于同一点;
议一议
在纸上画出一个直角三角形。
(1)画出直角三角形的三条高,
(2)它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
A
B
C
D
议一议
(1) 你能画出钝角三角形的三条高吗?
(2)钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点。
(3)它们所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点。
A
B
C
D
F
O
E
【总结归纳】三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
做一做:
请拿出课前准备的锐角三角形纸片.
(1)你能画出这个三角形的三条高吗?
(2)你能用折纸的方法得到它们吗?
(3)这三条高之间有怎样的位置关系?
O
A
B
C
D
E
F
锐角三角形的三条高交于 .
一点
(三角形内部)
探究新知
可借助优教平台的“【探究动画】三角形的高和垂心” 互动资源,动态、直观、辅助探究与发现.
猜一猜:直角三角形的三条高之间有怎样的位置关系?
画一画:请你画出直角三角形的三条高,并验证猜想.
探究新知
A
B
C
D
填一填:如图,在△ABC中,∠ABC=90°,BD⊥AC
(1)直角边BC边上的高是 ;
(2)直角边AB边上的高是 ;
(3)斜边AC边上的高是________.
AB
BC
BD
直角三角形的三条高交于 .
一点
(直角顶点)
可借助优教平台的“【探究动画】三角形的高和垂心” 互动资源,动态、直观、辅助探究与发现.
画一画:你能画出钝角三角形的三条高吗?
钝角三角形的三条高不交于一点;
但它们所在的直线交于三角形外部一点.
想一想:钝角三角形的三条高交于一点吗? 它们所在的直线交于一点吗?
A
B
C
D
E
F
O
填一填:如图,在△ABC中,∠ABC>90°
AB边上的高是 ;
BC边上的高是 ;
CA边上的高是 .
CF
AD
BE
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
探究新知
可借助优教平台的“【探究动画】三角形的高和垂心” 互动资源,动态、直观、辅助探究与发现.
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在的直线的交点的位置
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
探究归纳
三角形的三条高所在的直线交于一点.
(垂心)
1.分别指出直角△ABC 的三条高。
AB边
CB边
A
B
C
D
直角边BC边上的高是 ;
直角边AB边上的高是 ;
斜边AC边上的高是 。
BD
2.分别指出钝角△ABC 的三条高。
A
B
C
D
E
F
CE
AD
AB边上的高是 ;
BC边上的高是 ;
CA边上的高是 ;
BF
3.下列结论:①三角形的角平分线、中线、高都是线段;
②直角三角形只有一条高;
③三角形的中线可能在三角形外部;
④三角形的高都在三角形内部.
其中正确的有( )
A.1个 B.2个
C.3个 D.4个
A
4.如图所示,在△ABC中,BC边上的高 ,AB边上的高是 ;
在△BCE中,BE边上的高是 ;EC边上的高是 ;
在△ACD中,AC边上的高是 ; CD边上的高是 .
AF
CE
CE
BE
CD
AC
5.在△ABC中,AD是边BC上的高,也是∠BAC的角平分线,若∠B=40°,求∠BAC的度数.
在△ABC中,
∵AD是边BC上的高
∴AD⊥BC,
∴∠ADB=90°
在Rt△ABD中,∠ADB=90°,∠B=40°
∴∠BAD=90°-∠B=90°-40°=50°
又∵AD是∠BAC 的角平分线
∴∠BAC=2∠BAD=100°
5.在△ABC中,AD是边BC上的高,也是∠BAC的角平分线,若∠B=40°,求∠BAC的度数.
三角形的高
锐角三角形的三条高
都在三角形的内部.
高的定义
高的性质
直角三角形的三条高
交于直角顶点.
钝角三角形的三条高
所在直线交于一点.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
在三角形中,连接一个顶点与它对边中点的线段。
3.三角形的三条中线__________
2.填一填
∵BE是中线,∴_____=_____=
∵CF是中线,∴AB=2____=2____
AE
CE
AC
1
2
1.三角形的中线:
AF
BF
交于一点
5.填一填
∵BE是△ABC的角平分线,∠ABE=______
∵CF是△ABC的角平分线,∴∠ACB=2______=2______
∠CBE
∠ACF
∠BCF
4.三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
1 认识三角形
第4课时 三角形的高线
1.理解三角形高的相关概念,会在具体的三角形中画高,尤其是钝角三角形的高.
2.经历探索三角形三条高之间位置关系的过程.
3.体会类比、猜想、实验、归纳等数学思维方法.
学习目标
下面的三角形房梁中,立柱与横梁有什么特殊的位置关系?
立
柱
横梁
试着用三角形表示。
A
B
C
F
AF⊥BC
A
B
C
F
【思考】AF叫做什么?
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
如图, 线段AF是BC边上的高.
【想一想】三角形有几条高?
一个三角形有三个顶点,应该有三条高.
∵AF是△ABC的高
∴∠AFB =∠AFC =90°
符号语言:
反之:
∵∠AFB =90°(∠AFC =90°)
∴AF 是△ABC的高
要标明垂直的记号和垂足的字母!
做一做
每人准备一个锐角三角形纸片。
(1) 你能画出这个三角形的三条高吗
(2) 你能用折纸的办法得到它们吗
使折痕过顶点,顶点的对边边缘重合
(3) 这三条高之间有怎样的位置关系?
锐角三角形的三条高交于同一点;
议一议
在纸上画出一个直角三角形。
(1)画出直角三角形的三条高,
(2)它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
A
B
C
D
议一议
(1) 你能画出钝角三角形的三条高吗?
(2)钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点。
(3)它们所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点。
A
B
C
D
F
O
E
【总结归纳】三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
做一做:
请拿出课前准备的锐角三角形纸片.
(1)你能画出这个三角形的三条高吗?
(2)你能用折纸的方法得到它们吗?
(3)这三条高之间有怎样的位置关系?
O
A
B
C
D
E
F
锐角三角形的三条高交于 .
一点
(三角形内部)
探究新知
可借助优教平台的“【探究动画】三角形的高和垂心” 互动资源,动态、直观、辅助探究与发现.
猜一猜:直角三角形的三条高之间有怎样的位置关系?
画一画:请你画出直角三角形的三条高,并验证猜想.
探究新知
A
B
C
D
填一填:如图,在△ABC中,∠ABC=90°,BD⊥AC
(1)直角边BC边上的高是 ;
(2)直角边AB边上的高是 ;
(3)斜边AC边上的高是________.
AB
BC
BD
直角三角形的三条高交于 .
一点
(直角顶点)
可借助优教平台的“【探究动画】三角形的高和垂心” 互动资源,动态、直观、辅助探究与发现.
画一画:你能画出钝角三角形的三条高吗?
钝角三角形的三条高不交于一点;
但它们所在的直线交于三角形外部一点.
想一想:钝角三角形的三条高交于一点吗? 它们所在的直线交于一点吗?
A
B
C
D
E
F
O
填一填:如图,在△ABC中,∠ABC>90°
AB边上的高是 ;
BC边上的高是 ;
CA边上的高是 .
CF
AD
BE
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
探究新知
可借助优教平台的“【探究动画】三角形的高和垂心” 互动资源,动态、直观、辅助探究与发现.
锐角三角形 直角三角形 钝角三角形
高在三角形内部的数量
高之间是否相交
高所在的直线是否相交
三条高所在的直线的交点的位置
3
1
1
相交
相交
不相交
相交
相交
相交
三角形内部
直角顶点
三角形外部
探究归纳
三角形的三条高所在的直线交于一点.
(垂心)
1.分别指出直角△ABC 的三条高。
AB边
CB边
A
B
C
D
直角边BC边上的高是 ;
直角边AB边上的高是 ;
斜边AC边上的高是 。
BD
2.分别指出钝角△ABC 的三条高。
A
B
C
D
E
F
CE
AD
AB边上的高是 ;
BC边上的高是 ;
CA边上的高是 ;
BF
3.下列结论:①三角形的角平分线、中线、高都是线段;
②直角三角形只有一条高;
③三角形的中线可能在三角形外部;
④三角形的高都在三角形内部.
其中正确的有( )
A.1个 B.2个
C.3个 D.4个
A
4.如图所示,在△ABC中,BC边上的高 ,AB边上的高是 ;
在△BCE中,BE边上的高是 ;EC边上的高是 ;
在△ACD中,AC边上的高是 ; CD边上的高是 .
AF
CE
CE
BE
CD
AC
5.在△ABC中,AD是边BC上的高,也是∠BAC的角平分线,若∠B=40°,求∠BAC的度数.
在△ABC中,
∵AD是边BC上的高
∴AD⊥BC,
∴∠ADB=90°
在Rt△ABD中,∠ADB=90°,∠B=40°
∴∠BAD=90°-∠B=90°-40°=50°
又∵AD是∠BAC 的角平分线
∴∠BAC=2∠BAD=100°
5.在△ABC中,AD是边BC上的高,也是∠BAC的角平分线,若∠B=40°,求∠BAC的度数.
三角形的高
锐角三角形的三条高
都在三角形的内部.
高的定义
高的性质
直角三角形的三条高
交于直角顶点.
钝角三角形的三条高
所在直线交于一点.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
