4.3.2 利用“角边角”“角角边”判定三角形全等 课件(共25张PPT)
文档属性
| 名称 | 4.3.2 利用“角边角”“角角边”判定三角形全等 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 07:55:27 | ||
图片预览






文档简介
(共25张PPT)
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适
你能说明其中理由吗
3
2
1
情境引入
探索三角形全等的条件
三条边
两角一边
两边一角
三个角
一个条件
一条边
一个角
两个条件
两角
两条边
一边一角
三个条件
情境引入
3 探索三角形全等的条件
第2课时 利用“角边角”“角角边”判定三角形全等
1.通过画图、猜想、验证、交流,探索三角形全等的“角边角”条件.
2.通过独立思考、合作交流、推理得出三角形全等的“角角边”条件,体现转化和推理的思想.
3.会利用“ASA”和“AAS”通过简单的推理判别两个三角形全等,从而解决一些简单的实际问题.
学习目标
小明在家锻炼时,不小心用球将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢 如果可以,带哪块去合适 为什么
请同学们帮他想一想.
探究新知
A
B
只给出一个或两个条件时,是不能保证做出的三角形与原来三角形全等的.
要保证做出的三角形与原来三角形全等,至少需要边或角的三个条件:
(1)三个角
(2)三条边
(3)两角一边
(4)两边一角
SSS
不能!
探究新知
探究新知
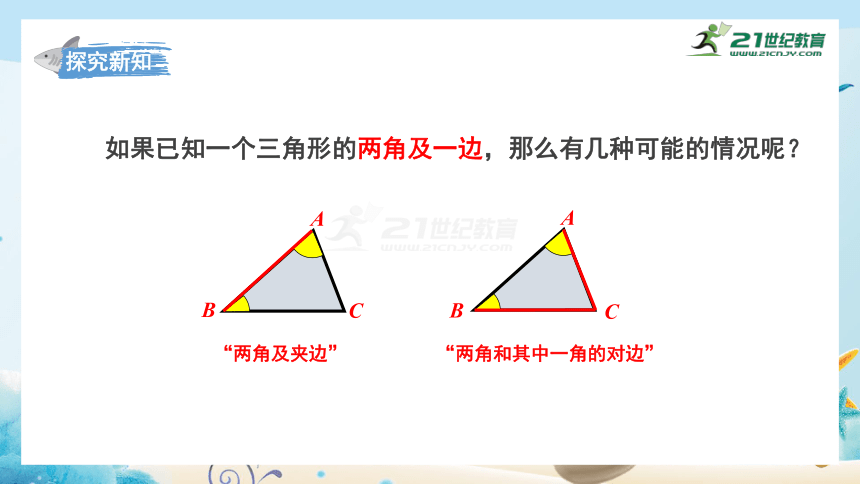
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
“两角及夹边”
“两角和其中一角的对边”
探究新知
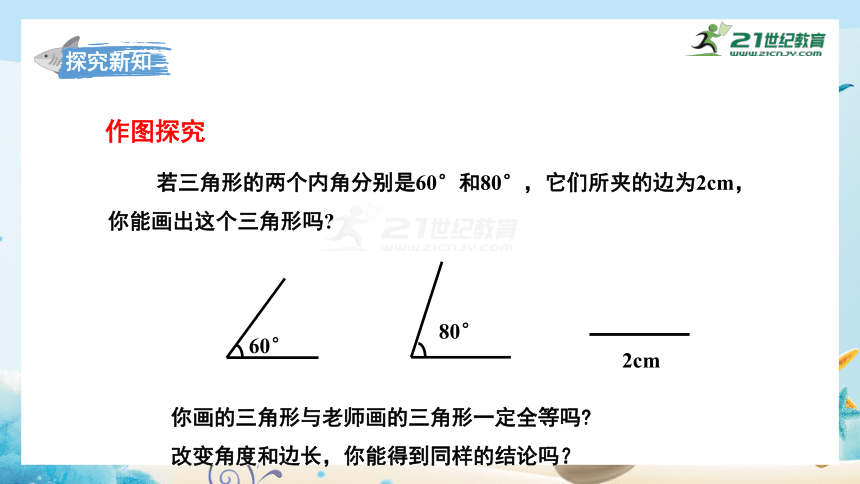
作图探究
若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
2cm
60°
80°
你画的三角形与老师画的三角形一定全等吗
改变角度和边长,你能得到同样的结论吗?
判定三角形全等的方法:
探究新知
两角及其夹边分别相等的两个三角形全等.
简写成“角边角”或“ASA”
几何语言:
在△ABC 和△ A′B′ C′中,
∴△ABC ≌△ A′B′ C′(ASA).
∠A =∠A′,
AB = A′B′,
∠B =∠B′,
A
B
C
A'
B'
C'
问题1. 画线段AB=10cm,再画∠BAP=60°,∠ABQ=80°,AP与BQ相交于点C. 剪下所画的△ABC在小组内进行比较. 你能得到什么结论?用语言描述你们的发现.
时间:3分钟
展示:以小组为单位进行展示
评价方式:自评、互评
评价标准:参与小组讨论得1
能得出结论得1
能代表小组展示1
(针对目标1)
探索新知
探索新知
问题2. 画线段 AB=16cm,再∠BAP=40°∠ABQ=30°,AP与BQ相交于点C.剪下所画的△ABC在小组内进行比较.你能得到什么结论?用语言描述你们的发现.
(针对目标1)
时间:3分钟
展示:以小组为单位进行展示
评价方式:自评、互评
评价标准:参与小组讨论得1
能得出结论得1
能代表小组展示1
△ABC ≌△DEF
____=____
BC EF
( )
在△ABC和△DEF中
简写为“角边角”或“ASA”.
∵
∴
∠B ∠E
∠C ∠F
ASA
“角边角”的判定方法
文字语言
两角及其夹边分别相等的两个三角形全等,
基本事实
几何语言
____=____
____=____
归纳结论
∠ABC=∠DCB ( )
= ( )
= ( )
∴ △ABC≌ ( )
∠ACB
∠DBC
△DCB
在△ABC和△DCB中
ASA
例1. 如图,∠ABC=∠DCB,∠ACB=∠DBC,AB和CD是否相等?试说明理由.
∵
已知
公共边
已知
解:AB=CD,理由如下:
∴ AB=CD( )
全等三角形的对应边相等
BC CB
(针对目标3)
A
B
C
D
评价方式:自评、师评
评价标准:能正确填空得1
运用新知
问题1:观察图中两个三角形,有哪些相等的条件?
问题2:这样的两个三角形全等吗?
问题3:你能解释你的发现吗?
(针对目标2)
探索新知
问题4. 推理验证,如图在△ABC和△DEF中,∠B=∠E,∠C=∠F,AC=DF,请说明△ABC≌△DEF.
(针对目标2)
探索新知
时间:3分钟
展示:以小组为单位进行展示
评价方式:自评、互评
评价标准:参与小组讨论得1
能得出结论得1
能代表小组展示1
△ABC ≌△DEF
____=____
AC DF
( )
在△ABC和△DEF中
简写为“角角边”或“AAS”
∵
∴
∠B ∠E
∠C ∠F
AAS
“角角边”的判定方法
文字语言
基本事实
几何语言
____=____
____=____
两角分别相等且其中一组等角的对边相等的两个三角形全等
归纳结论
例3、已知:如图AB=AC,BD=CD,请问△ABD与△ACD全等吗?
例2. 如图,AB 与 CD 相交与点 O,O 是 AB 的中点,∠C=∠D,△AOC 与△BOD 全等吗?为什么?
(针对目标3)
评价方式:自评、互评
评价标准:能说明全等的理由得1
能通过同学的讲解理解全等的理由得1
拓展创新
如图∠ABC=∠DCB, 试添加一个条件,使得△ ABC≌△DCB,这个条件可以是 或 . 并选择其中一个条件加以证明.
∠A=∠D
∠ACB=∠DBC
(针对目标3)
评价方式:自评、互评
评价标准:每添加一个条件得1
能说明全等的理由得1
能通过同学的讲解理解全等的理由得1
拓展创新
1.如图,已知AB=DE,∠A=∠D , ∠C=∠F, 则△ABC≌△DEF的理由是:________________
AAS
(针对目标3)
评价方式:自评
评价标准:能独立得出正确答案得1
能通过同学讲解找到自己错误的原因得1
当堂检测
2.如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适
你能说明其中理由吗
3
2
1
问题解决
3.已知:∠C=∠E,∠1=∠2,AB=AD,BC和DE相等吗?为什么?
评价方式:自评
评价标准:能独立得出正确答案得1
能通过同学讲解找到自己错误的原因得1
(针对目标3)
当堂检测
本节课我收获了
1.探讨了什么问题?
2.得出了什么结论?
3.运用了什么方法?
4.体会了什么思想?
越分享越富有,本节课我们:
课堂小结
1、必做题(9颗 及以下同学)
2、选做题(10颗 及以上同学)
已知:如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
试说明:(1)△BDA≌△AEC;(2)DE=BD+CE.
课本习题4.7 1、2、3、4题
分层作业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适
你能说明其中理由吗
3
2
1
情境引入
探索三角形全等的条件
三条边
两角一边
两边一角
三个角
一个条件
一条边
一个角
两个条件
两角
两条边
一边一角
三个条件
情境引入
3 探索三角形全等的条件
第2课时 利用“角边角”“角角边”判定三角形全等
1.通过画图、猜想、验证、交流,探索三角形全等的“角边角”条件.
2.通过独立思考、合作交流、推理得出三角形全等的“角角边”条件,体现转化和推理的思想.
3.会利用“ASA”和“AAS”通过简单的推理判别两个三角形全等,从而解决一些简单的实际问题.
学习目标
小明在家锻炼时,不小心用球将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢 如果可以,带哪块去合适 为什么
请同学们帮他想一想.
探究新知
A
B
只给出一个或两个条件时,是不能保证做出的三角形与原来三角形全等的.
要保证做出的三角形与原来三角形全等,至少需要边或角的三个条件:
(1)三个角
(2)三条边
(3)两角一边
(4)两边一角
SSS
不能!
探究新知
探究新知
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
“两角及夹边”
“两角和其中一角的对边”
探究新知
作图探究
若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗
2cm
60°
80°
你画的三角形与老师画的三角形一定全等吗
改变角度和边长,你能得到同样的结论吗?
判定三角形全等的方法:
探究新知
两角及其夹边分别相等的两个三角形全等.
简写成“角边角”或“ASA”
几何语言:
在△ABC 和△ A′B′ C′中,
∴△ABC ≌△ A′B′ C′(ASA).
∠A =∠A′,
AB = A′B′,
∠B =∠B′,
A
B
C
A'
B'
C'
问题1. 画线段AB=10cm,再画∠BAP=60°,∠ABQ=80°,AP与BQ相交于点C. 剪下所画的△ABC在小组内进行比较. 你能得到什么结论?用语言描述你们的发现.
时间:3分钟
展示:以小组为单位进行展示
评价方式:自评、互评
评价标准:参与小组讨论得1
能得出结论得1
能代表小组展示1
(针对目标1)
探索新知
探索新知
问题2. 画线段 AB=16cm,再∠BAP=40°∠ABQ=30°,AP与BQ相交于点C.剪下所画的△ABC在小组内进行比较.你能得到什么结论?用语言描述你们的发现.
(针对目标1)
时间:3分钟
展示:以小组为单位进行展示
评价方式:自评、互评
评价标准:参与小组讨论得1
能得出结论得1
能代表小组展示1
△ABC ≌△DEF
____=____
BC EF
( )
在△ABC和△DEF中
简写为“角边角”或“ASA”.
∵
∴
∠B ∠E
∠C ∠F
ASA
“角边角”的判定方法
文字语言
两角及其夹边分别相等的两个三角形全等,
基本事实
几何语言
____=____
____=____
归纳结论
∠ABC=∠DCB ( )
= ( )
= ( )
∴ △ABC≌ ( )
∠ACB
∠DBC
△DCB
在△ABC和△DCB中
ASA
例1. 如图,∠ABC=∠DCB,∠ACB=∠DBC,AB和CD是否相等?试说明理由.
∵
已知
公共边
已知
解:AB=CD,理由如下:
∴ AB=CD( )
全等三角形的对应边相等
BC CB
(针对目标3)
A
B
C
D
评价方式:自评、师评
评价标准:能正确填空得1
运用新知
问题1:观察图中两个三角形,有哪些相等的条件?
问题2:这样的两个三角形全等吗?
问题3:你能解释你的发现吗?
(针对目标2)
探索新知
问题4. 推理验证,如图在△ABC和△DEF中,∠B=∠E,∠C=∠F,AC=DF,请说明△ABC≌△DEF.
(针对目标2)
探索新知
时间:3分钟
展示:以小组为单位进行展示
评价方式:自评、互评
评价标准:参与小组讨论得1
能得出结论得1
能代表小组展示1
△ABC ≌△DEF
____=____
AC DF
( )
在△ABC和△DEF中
简写为“角角边”或“AAS”
∵
∴
∠B ∠E
∠C ∠F
AAS
“角角边”的判定方法
文字语言
基本事实
几何语言
____=____
____=____
两角分别相等且其中一组等角的对边相等的两个三角形全等
归纳结论
例3、已知:如图AB=AC,BD=CD,请问△ABD与△ACD全等吗?
例2. 如图,AB 与 CD 相交与点 O,O 是 AB 的中点,∠C=∠D,△AOC 与△BOD 全等吗?为什么?
(针对目标3)
评价方式:自评、互评
评价标准:能说明全等的理由得1
能通过同学的讲解理解全等的理由得1
拓展创新
如图∠ABC=∠DCB, 试添加一个条件,使得△ ABC≌△DCB,这个条件可以是 或 . 并选择其中一个条件加以证明.
∠A=∠D
∠ACB=∠DBC
(针对目标3)
评价方式:自评、互评
评价标准:每添加一个条件得1
能说明全等的理由得1
能通过同学的讲解理解全等的理由得1
拓展创新
1.如图,已知AB=DE,∠A=∠D , ∠C=∠F, 则△ABC≌△DEF的理由是:________________
AAS
(针对目标3)
评价方式:自评
评价标准:能独立得出正确答案得1
能通过同学讲解找到自己错误的原因得1
当堂检测
2.如图,小明不慎将一块三角形玻璃打碎为三块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗 如果可以,带哪块去合适
你能说明其中理由吗
3
2
1
问题解决
3.已知:∠C=∠E,∠1=∠2,AB=AD,BC和DE相等吗?为什么?
评价方式:自评
评价标准:能独立得出正确答案得1
能通过同学讲解找到自己错误的原因得1
(针对目标3)
当堂检测
本节课我收获了
1.探讨了什么问题?
2.得出了什么结论?
3.运用了什么方法?
4.体会了什么思想?
越分享越富有,本节课我们:
课堂小结
1、必做题(9颗 及以下同学)
2、选做题(10颗 及以上同学)
已知:如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.
试说明:(1)△BDA≌△AEC;(2)DE=BD+CE.
课本习题4.7 1、2、3、4题
分层作业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
