3.2.1 旋转的定义和性质 课件(共31张PPT)
文档属性
| 名称 | 3.2.1 旋转的定义和性质 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 09:05:28 | ||
图片预览









文档简介
(共31张PPT)
这些运动有什么共同的特点?
情景引入
这些运动有什么共同的特点?
情景引入
这些运动有什么共同的特点?
情景引入
这些运动有什么共同的特点?
情景引入
2 图形的旋转
第1课时 旋转的定义和性质
1.掌握旋转的有关概念及基本性质.
2.能够根据旋转的基本性质解决实际问题.
学习目标
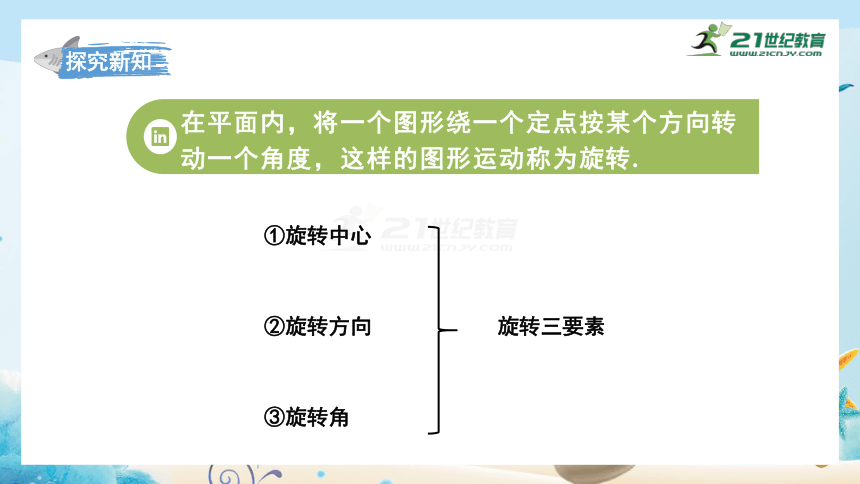
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
①旋转中心
②旋转方向
③旋转角
旋转三要素
探究新知
下列现象属于旋转的是( )
A.摩托车在急刹车时向前滑动
B.在空中上升的氢气球
C.幸运大转盘转动的过程
D.笔直的铁轨上飞驰而过的火车
C
学以致用
C
A
B
O
D
△ABO绕点O顺时针旋转某个角度得到△CDO,则:
点B的对应点是点_____;
线段OB的对应线段是线段______;
线段AB的对应线段是线段______;
∠A的对应角是______;
∠B的对应角是______;
旋转中心是点______;
旋转的角是_______________ .
写出图中相等的线段和相等的角_____________ .
D
OD
CD
∠C
∠D
O
∠AOC、∠BOD
学以致用
自主尝试列举
旋转的性质
①旋转前后两图形全等
(对应线段相等;对应角相等)
②对应点到旋转中心的距离相等
③任意一组对应点到旋转中心的连线所成的角都等于旋转角
学以致用
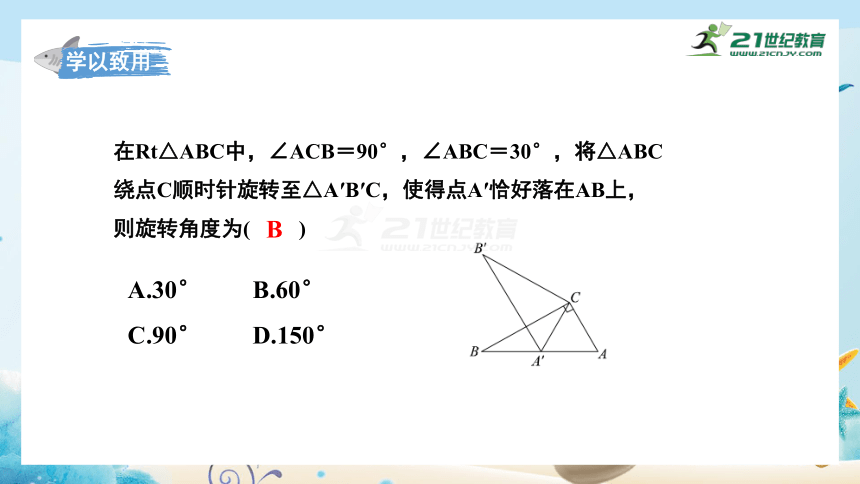
在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30° B.60°
C.90° D.150°
B
学以致用
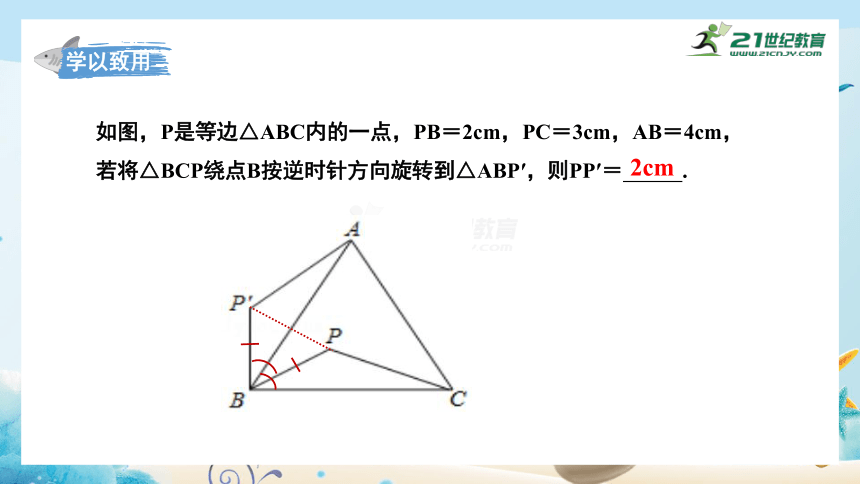
如图,P是等边△ABC内的一点,PB=2cm,PC=3cm,AB=4cm,若将△BCP绕点B按逆时针方向旋转到△ABP′,则PP′= .
2cm
学以致用
F
B
C
D
E
以上情景中的运动是一种什么现象,有什么共同特征?你能否描述一下什么叫旋转?
你能类比平移描述一下什么叫旋转吗?
合作探究
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
旋转的定义:
这个定点称为旋转中心.
旋转方向分为顺时针与逆时针.
转动的角称为旋转角.
总结概念
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
温馨提示:
①“旋转中心,旋转方向,旋转角度”称之为旋转的三要素;
②旋转不改变图形的形状和大小,旋转变换同样属于全等变换.
归纳总结
你能举出一些生活中类似旋转现象的例子吗?
合作探究
B
O
A
45
°
点A绕 点,按 方向,转动了 度到点B.
O
顺时针
45
合作探究
A
B
O
C
D
点A的对应点是________;
旋转中心是________;
旋转角是_________________;
(1)如图,△ABO绕点O旋转得到△CDO, 则:
点C
点O
∠AOC,
∠BOD
如何定义旋转角?
对应点与旋转中心所连线段的夹角.
找一找
B
A
B
A
C
C
O
100
0
旋转中心
旋转角度
旋转方向
旋转的三要素?
△ABC绕 点,按 方向,转动了 度到△A’B’C’ .
O
顺时针
100
合作探究
A
B
C
B′
C′
O
A
B
C
·
A′
B′
C′
旋转前、后的图形全等.
即对应角相等,对应边相等.
对应点到旋转中心的距离相等. 对应点与旋转中心的连线所成的角都等于旋转角.
观察后你有什么发现?
合作探究
如图3-11,两张透明纸上的四边形ABCD和四边形EFGH完全重合,在纸上选取旋转中心O,并将其固定. 把其中一张纸片绕点O旋转一定角度(如图3-12).
(1)观察图3-12的两个四边形,你能发现有哪些相等的线段和相等的角?
(2)连接AO,BO,CO,DO,EO,FO,GO,HO,你又能发现有哪些相等的线段和相等的角?
(3)在图3-12中再取一些对应点,画出它们与旋转中心所连成的线段你又能发现什么?
改变透明纸上所画图形的形状,再试一试,并与同伴交流.
合作探究
旋转的性质:“三特点”
1、对应点到旋转中心的距离相等;
2、对应点与旋转中心的连线所成的角(都相等)都是旋转角;
3、对应线段相等;对应角相等.
合作探究
例1. 如图6,正方形ABCD中,E、F分别是AB、BC边上的点,∠EDF=45°,将△DAE绕点D按逆时针方向旋转到△DCM . 求∠FDM的度数.
学以致用
(1)旋转中心是哪一点
(2)旋转角是多少度
如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
A
B
F
C
E
D
(3)∠EAF等于多少度
(4)经过旋转,点B与点E分别转到什么位置
点A
90°
90°
点D、点F
针对练习
图案的欣赏与设计
美图欣赏
美图欣赏
通过本节课的学习,你有什么收获?
课堂小结
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
2. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C.平移图形可以向某方向旋转一定距离得到
D.由平移得到的图形也一定可由旋转得到
B
C
当堂检测
3、如图,在Rt△ABC中,∠ACB=90°,∠B=30°将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE.
(1)点B的对应点是______,AC对应线段是_________.
(2)判断△ACD的形状.
当堂检测
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
这些运动有什么共同的特点?
情景引入
这些运动有什么共同的特点?
情景引入
这些运动有什么共同的特点?
情景引入
这些运动有什么共同的特点?
情景引入
2 图形的旋转
第1课时 旋转的定义和性质
1.掌握旋转的有关概念及基本性质.
2.能够根据旋转的基本性质解决实际问题.
学习目标
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
①旋转中心
②旋转方向
③旋转角
旋转三要素
探究新知
下列现象属于旋转的是( )
A.摩托车在急刹车时向前滑动
B.在空中上升的氢气球
C.幸运大转盘转动的过程
D.笔直的铁轨上飞驰而过的火车
C
学以致用
C
A
B
O
D
△ABO绕点O顺时针旋转某个角度得到△CDO,则:
点B的对应点是点_____;
线段OB的对应线段是线段______;
线段AB的对应线段是线段______;
∠A的对应角是______;
∠B的对应角是______;
旋转中心是点______;
旋转的角是_______________ .
写出图中相等的线段和相等的角_____________ .
D
OD
CD
∠C
∠D
O
∠AOC、∠BOD
学以致用
自主尝试列举
旋转的性质
①旋转前后两图形全等
(对应线段相等;对应角相等)
②对应点到旋转中心的距离相等
③任意一组对应点到旋转中心的连线所成的角都等于旋转角
学以致用
在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为( )
A.30° B.60°
C.90° D.150°
B
学以致用
如图,P是等边△ABC内的一点,PB=2cm,PC=3cm,AB=4cm,若将△BCP绕点B按逆时针方向旋转到△ABP′,则PP′= .
2cm
学以致用
F
B
C
D
E
以上情景中的运动是一种什么现象,有什么共同特征?你能否描述一下什么叫旋转?
你能类比平移描述一下什么叫旋转吗?
合作探究
在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.
旋转的定义:
这个定点称为旋转中心.
旋转方向分为顺时针与逆时针.
转动的角称为旋转角.
总结概念
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时,
温馨提示:
①“旋转中心,旋转方向,旋转角度”称之为旋转的三要素;
②旋转不改变图形的形状和大小,旋转变换同样属于全等变换.
归纳总结
你能举出一些生活中类似旋转现象的例子吗?
合作探究
B
O
A
45
°
点A绕 点,按 方向,转动了 度到点B.
O
顺时针
45
合作探究
A
B
O
C
D
点A的对应点是________;
旋转中心是________;
旋转角是_________________;
(1)如图,△ABO绕点O旋转得到△CDO, 则:
点C
点O
∠AOC,
∠BOD
如何定义旋转角?
对应点与旋转中心所连线段的夹角.
找一找
B
A
B
A
C
C
O
100
0
旋转中心
旋转角度
旋转方向
旋转的三要素?
△ABC绕 点,按 方向,转动了 度到△A’B’C’ .
O
顺时针
100
合作探究
A
B
C
B′
C′
O
A
B
C
·
A′
B′
C′
旋转前、后的图形全等.
即对应角相等,对应边相等.
对应点到旋转中心的距离相等. 对应点与旋转中心的连线所成的角都等于旋转角.
观察后你有什么发现?
合作探究
如图3-11,两张透明纸上的四边形ABCD和四边形EFGH完全重合,在纸上选取旋转中心O,并将其固定. 把其中一张纸片绕点O旋转一定角度(如图3-12).
(1)观察图3-12的两个四边形,你能发现有哪些相等的线段和相等的角?
(2)连接AO,BO,CO,DO,EO,FO,GO,HO,你又能发现有哪些相等的线段和相等的角?
(3)在图3-12中再取一些对应点,画出它们与旋转中心所连成的线段你又能发现什么?
改变透明纸上所画图形的形状,再试一试,并与同伴交流.
合作探究
旋转的性质:“三特点”
1、对应点到旋转中心的距离相等;
2、对应点与旋转中心的连线所成的角(都相等)都是旋转角;
3、对应线段相等;对应角相等.
合作探究
例1. 如图6,正方形ABCD中,E、F分别是AB、BC边上的点,∠EDF=45°,将△DAE绕点D按逆时针方向旋转到△DCM . 求∠FDM的度数.
学以致用
(1)旋转中心是哪一点
(2)旋转角是多少度
如图,在正方形ABCD中,E是CB延长线上一点,△ABE经过旋转后得到△ADF,请按图回答:
A
B
F
C
E
D
(3)∠EAF等于多少度
(4)经过旋转,点B与点E分别转到什么位置
点A
90°
90°
点D、点F
针对练习
图案的欣赏与设计
美图欣赏
美图欣赏
通过本节课的学习,你有什么收获?
课堂小结
1.下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
2. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C.平移图形可以向某方向旋转一定距离得到
D.由平移得到的图形也一定可由旋转得到
B
C
当堂检测
3、如图,在Rt△ABC中,∠ACB=90°,∠B=30°将△ACB绕点A逆时针引旋转,使点A落在AB边上的点D,得到△DCE.
(1)点B的对应点是______,AC对应线段是_________.
(2)判断△ACD的形状.
当堂检测
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
