3.3 中心对称 课件(共36张PPT)
文档属性
| 名称 | 3.3 中心对称 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 14.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 08:27:28 | ||
图片预览








文档简介
(共36张PPT)
图形变换——全等变换
回顾与思考
轴对称变换
美图欣赏
成轴对称的两个图形的性质:
把一个图形沿着某一条直线折叠能与另一个图形完全重合,那么就说这两个图形关于这条直线对称或轴对称.
1.两个图形是全等形.
2.对称轴是对应点连线的垂直平分线.
旧知回顾
旋转变换
美图欣赏
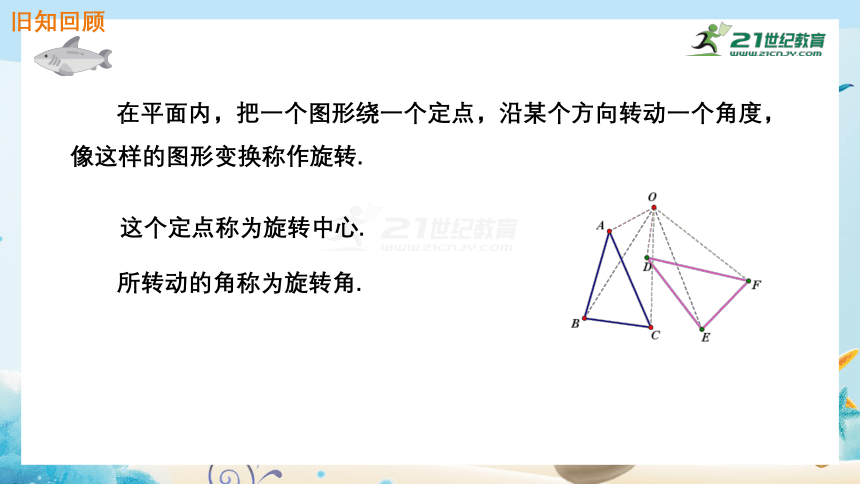
所转动的角称为旋转角.
在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形变换称作旋转.
这个定点称为旋转中心.
旧知回顾
3 中心对称
1.观察:了解中心对称的概念(抽象美)
2.操作:探索中心对称的性质(探索美)
3.欣赏:认识自然界和现实生活中的中心对称图形(欣赏美)
4.设计:积累数学活动经验,增强动手实践能力,发展空间观念(创造美)
学习目标
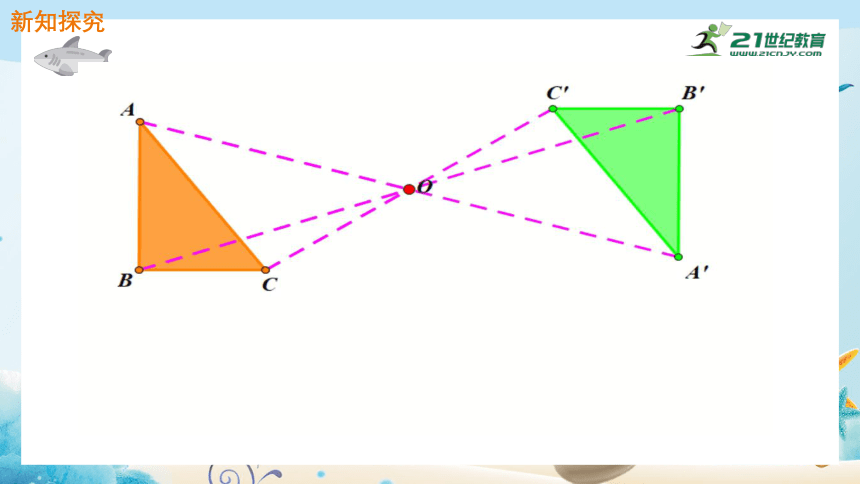
新知探究
B
C
O
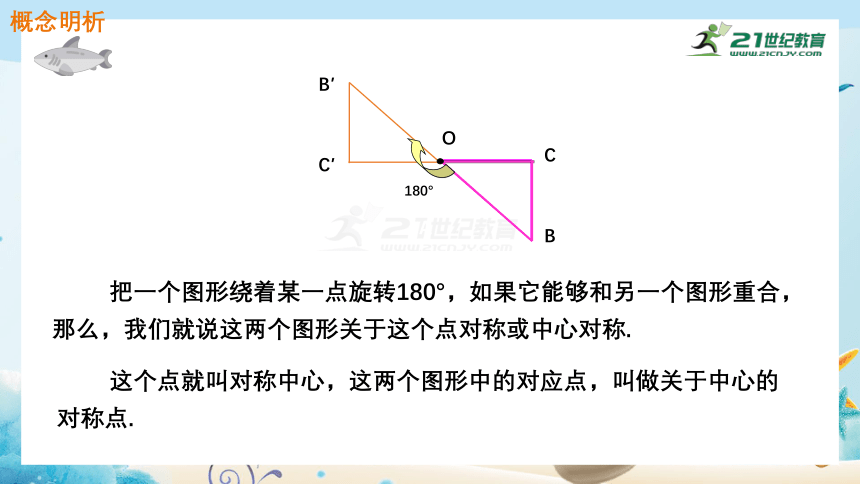
把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称.
C′
B′
A
180°
这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
概念明析
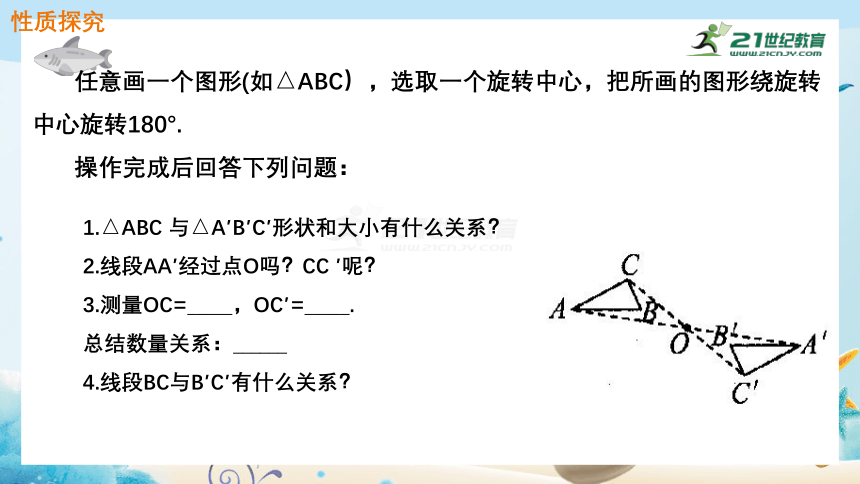
1.△ABC 与△A′B′C′形状和大小有什么关系?
2.线段AA′经过点O吗?CC ′呢?
3.测量OC=_____,OC′=_____.
总结数量关系:______
4.线段BC与B′C′有什么关系?
任意画一个图形(如△ABC),选取一个旋转中心,把所画的图形绕旋转中心旋转180°.
操作完成后回答下列问题:
性质探究
(1)中心对称的两个图形是全等形;
(2)对称点所连线段都经过对称中心;
(3) 对称点所连线段被对称中心所平分;
(4) 对应线段平行(或共线)且相等.
中心对称的性质:
性质探究
游戏时刻:每位同学都作为平面内的一个点,挑选三位同学参加游戏,甲同学作为对称中心,大家一起找乙的朋友丙.
探究应用
例 如图,点O是线段AE的中点,以点O为对称中心,画出与五边形 ABCDE成中心对称的图形.
解:如图,连接BO并延长至B,使得OB′=OB ;
连接CO并延长至C,使得OC′=OC;
连接DO并延长至D,使得OD′=OD;
顺次连接A,D′,C′,B′,E.
图形 AD′C′B′E就是以点O为对称中心、与五边形 ABCDE成中心对称的图形.
探究应用
如图,已知△ABC与△A′B′C′成中心对称,求作出它们的对称中心O.
A
B
C
A′
B′
C′
探究应用
A
B
C
A′
B′
C′
解法一:根据观察,B、B′及C、C′应是两组对应点,连结BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图).
O
探究应用
A
B
C
A′
B′
C′
解法二:根据观察,B、B′应是对应点,连结BB′,找出BB′的中点O,则点O即为所求(如图).
O
探究应用
例:如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形.
O
E
D
C
B
A
B'
C'
D'
解:如图,
连结BO,并延长至B',使OB'=OB;
连结CO,并延长至C',使OC'=OC;
连结DO,并延长至D',使OD'=OD;
顺次连接E,B',C',D',A.
图形EB'C'D'A就是以点O为对称中心、与正五边形成中心对称的图形.
典型例题
O
E
D
C
B
A
B’
C’
D’
O
E
D
C
B
A
B’
C’
D’
中心对称图形
中心对称
一分为二
合二为一
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
图形大变身
探究新知
下面那些图形是中心对称图形?
(1)
(4)
(3)
(2)
A
B
A
B
B
A
A
B
√
√
√
×
P83读一读
应用提高
中心对称与轴对称
轴对称 中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折后重合 图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
A
B
A
B
应用提高
魔术师把5张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某两张牌旋转180°.
魔术师解除蒙具后,看到扑克牌如下图,你知道是哪两张吗?
应用提高
(1)
(2)
至少旋转多少度与自身重合?
对比探究
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
A
B
C
D
O
中心对称图形的定义:
中心对称图形是指一个图形.
概念明晰
中心对称 中心对称图形
区别 两个全等图形之间的位置关系 一个图形本身成中心对称.
联系 如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形. 如果把中心对称图形对称的部分看成是两个图形,那么它们又关于对称中心成中心对称.
概念辨析
O
M
N
Q
p
G
A
B
C
F
D
E
中心对称
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
翻转后和另一个图形重合
旋转后和另一个图形重合
轴 对 称
A
B
C
C'
A'
B'
概念辨析
1.观察常见的几何图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(1)
(2) (3) (4) (6)
(5)
(1)
(3)
(2)
(4)
(5)
(6)
学以致用
2. 在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
学以致用
图(1)
图(2)
回归生活:揭秘魔术
你认识这些图标吗?
回归生活
回归生活
课堂小结
中心对称的性质
中心对称
中心对称图形
欣赏与设计
中心
对称
发现美、创造美
“对比”学习法
积极探索、不怕困难、化繁为简
一分为二、合二为一、辩证思维
1.下面有4个汽车标致图案,其中是中心对称图形的是( )
A.②③④ B.③④ C.④ D.②
2.下列图形中,是轴对称图形,但不是中心对称图形的是( )
A
B
D
C
C
D
随堂检测
3.如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABC成中心对称的三角形.
A'
解:如图,
延长AD至A', 使DA'=DA
连结CA'、 BA'
则△CBA'即为所求
随堂检测
课后作业
【必做题】
1.下列四张扑克牌图案,属于中心对称图形的是( )
A.
B.
C.
D.
2.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
图形变换——全等变换
回顾与思考
轴对称变换
美图欣赏
成轴对称的两个图形的性质:
把一个图形沿着某一条直线折叠能与另一个图形完全重合,那么就说这两个图形关于这条直线对称或轴对称.
1.两个图形是全等形.
2.对称轴是对应点连线的垂直平分线.
旧知回顾
旋转变换
美图欣赏
所转动的角称为旋转角.
在平面内,把一个图形绕一个定点,沿某个方向转动一个角度,像这样的图形变换称作旋转.
这个定点称为旋转中心.
旧知回顾
3 中心对称
1.观察:了解中心对称的概念(抽象美)
2.操作:探索中心对称的性质(探索美)
3.欣赏:认识自然界和现实生活中的中心对称图形(欣赏美)
4.设计:积累数学活动经验,增强动手实践能力,发展空间观念(创造美)
学习目标
新知探究
B
C
O
把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就说这两个图形关于这个点对称或中心对称.
C′
B′
A
180°
这个点就叫对称中心,这两个图形中的对应点,叫做关于中心的对称点.
概念明析
1.△ABC 与△A′B′C′形状和大小有什么关系?
2.线段AA′经过点O吗?CC ′呢?
3.测量OC=_____,OC′=_____.
总结数量关系:______
4.线段BC与B′C′有什么关系?
任意画一个图形(如△ABC),选取一个旋转中心,把所画的图形绕旋转中心旋转180°.
操作完成后回答下列问题:
性质探究
(1)中心对称的两个图形是全等形;
(2)对称点所连线段都经过对称中心;
(3) 对称点所连线段被对称中心所平分;
(4) 对应线段平行(或共线)且相等.
中心对称的性质:
性质探究
游戏时刻:每位同学都作为平面内的一个点,挑选三位同学参加游戏,甲同学作为对称中心,大家一起找乙的朋友丙.
探究应用
例 如图,点O是线段AE的中点,以点O为对称中心,画出与五边形 ABCDE成中心对称的图形.
解:如图,连接BO并延长至B,使得OB′=OB ;
连接CO并延长至C,使得OC′=OC;
连接DO并延长至D,使得OD′=OD;
顺次连接A,D′,C′,B′,E.
图形 AD′C′B′E就是以点O为对称中心、与五边形 ABCDE成中心对称的图形.
探究应用
如图,已知△ABC与△A′B′C′成中心对称,求作出它们的对称中心O.
A
B
C
A′
B′
C′
探究应用
A
B
C
A′
B′
C′
解法一:根据观察,B、B′及C、C′应是两组对应点,连结BB′、CC′,BB′、CC′相交于点O,则点O即为所求(如图).
O
探究应用
A
B
C
A′
B′
C′
解法二:根据观察,B、B′应是对应点,连结BB′,找出BB′的中点O,则点O即为所求(如图).
O
探究应用
例:如图,点O是线段AE的中点,以点O为对称中心,画出与五边形ABCDE成中心对称的图形.
O
E
D
C
B
A
B'
C'
D'
解:如图,
连结BO,并延长至B',使OB'=OB;
连结CO,并延长至C',使OC'=OC;
连结DO,并延长至D',使OD'=OD;
顺次连接E,B',C',D',A.
图形EB'C'D'A就是以点O为对称中心、与正五边形成中心对称的图形.
典型例题
O
E
D
C
B
A
B’
C’
D’
O
E
D
C
B
A
B’
C’
D’
中心对称图形
中心对称
一分为二
合二为一
把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
图形大变身
探究新知
下面那些图形是中心对称图形?
(1)
(4)
(3)
(2)
A
B
A
B
B
A
A
B
√
√
√
×
P83读一读
应用提高
中心对称与轴对称
轴对称 中心对称
有一条对称轴——直线 有一个对称中心——点
图形沿对称轴对折后重合 图形绕对称中心旋转180°后重合
对称点的连线被对称轴垂直平分 对称点连线经过对称中心,且被对称中心平分
A
B
A
B
应用提高
魔术师把5张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某两张牌旋转180°.
魔术师解除蒙具后,看到扑克牌如下图,你知道是哪两张吗?
应用提高
(1)
(2)
至少旋转多少度与自身重合?
对比探究
把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
A
B
C
D
O
中心对称图形的定义:
中心对称图形是指一个图形.
概念明晰
中心对称 中心对称图形
区别 两个全等图形之间的位置关系 一个图形本身成中心对称.
联系 如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形. 如果把中心对称图形对称的部分看成是两个图形,那么它们又关于对称中心成中心对称.
概念辨析
O
M
N
Q
p
G
A
B
C
F
D
E
中心对称
有一条对称轴
——
直线
有一个对称中心
——
点
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
翻转后和另一个图形重合
旋转后和另一个图形重合
轴 对 称
A
B
C
C'
A'
B'
概念辨析
1.观察常见的几何图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
(1)
(2) (3) (4) (6)
(5)
(1)
(3)
(2)
(4)
(5)
(6)
学以致用
2. 在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
学以致用
图(1)
图(2)
回归生活:揭秘魔术
你认识这些图标吗?
回归生活
回归生活
课堂小结
中心对称的性质
中心对称
中心对称图形
欣赏与设计
中心
对称
发现美、创造美
“对比”学习法
积极探索、不怕困难、化繁为简
一分为二、合二为一、辩证思维
1.下面有4个汽车标致图案,其中是中心对称图形的是( )
A.②③④ B.③④ C.④ D.②
2.下列图形中,是轴对称图形,但不是中心对称图形的是( )
A
B
D
C
C
D
随堂检测
3.如图,已知AD是△ABC的中线,画出以点D为对称中心,与△ABC成中心对称的三角形.
A'
解:如图,
延长AD至A', 使DA'=DA
连结CA'、 BA'
则△CBA'即为所求
随堂检测
课后作业
【必做题】
1.下列四张扑克牌图案,属于中心对称图形的是( )
A.
B.
C.
D.
2.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
