4.3公式法(第2课时) 课件(共19张PPT)
文档属性
| 名称 | 4.3公式法(第2课时) 课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 08:25:36 | ||
图片预览





文档简介
(共19张PPT)
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式
a2-b2=(a+b)(a-b)
导入新课
4.3 公式法(2)
学习目标
1.理解并掌握用完全平方公式分解因式.(重点)
2.灵活应用各种方法分解因式,并能利用因式分解进行计算.(难点)
用完全平方公式分解因式
一
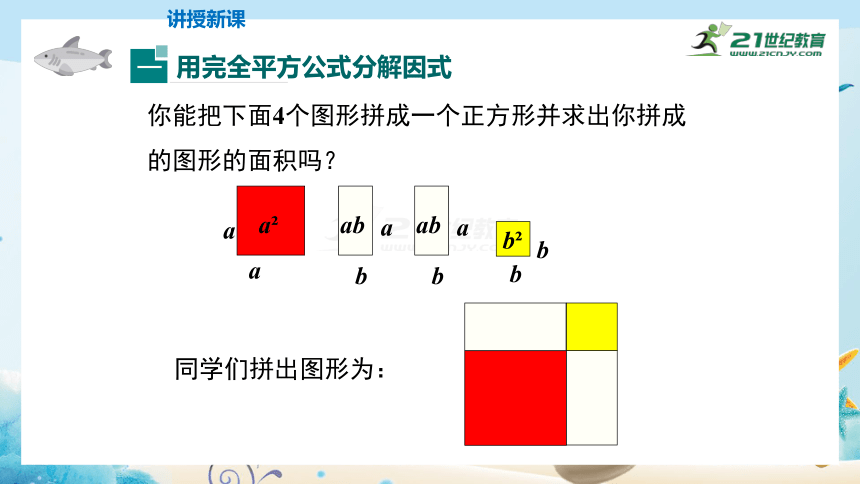
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a
b
ab
讲授新课
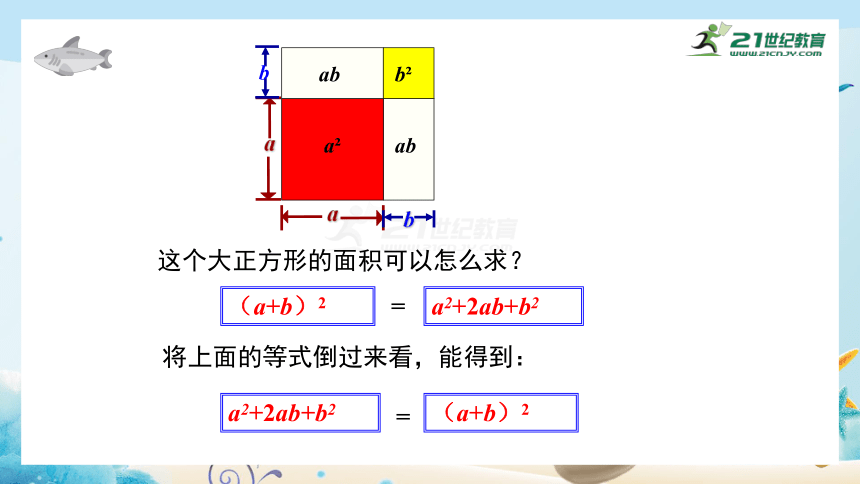
这个大正方形的面积可以怎么求?
a2+2ab+b2
(a+b)2
=
a
b
a
b
a
ab
ab
b
(a+b)2
a2+2ab+b2
=
将上面的等式倒过来看,能得到:
a2+2ab+b2
a2-2ab+b2
我们把a +2ab+b 和a -2ab+b 这样的式子叫作完全平方式.
观察这两个式子:
(1)每个多项式有几项?
(3)中间项和第一项,第三项有什么关系?
(2)每个多项式的第一项和第三项有什么特征?
三项
这两项都是数或式的平方,并且符号相同
是第一项和第三项底数的积的±2倍
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个同号的数或式的平方;
3.中间有两底数之积的±2倍.
完全平方式:
简记口诀:
首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a ± b)
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
3.a +4ab+4b =( ) +2· ( ) ·( )+( ) =( )
2.m -6m+9=( ) - 2· ( ) ·( )+( ) =( )
1. x +4x+4= ( ) +2·( )·( )+( ) =( )
x
2
x + 2
a
a 2b
a + 2b
2b
对照 a ±2ab+b =(a±b) ,填空:
m
m - 3
3
x
2
m
3
下列各式是不是完全平方式?
(1)a2-4a+4; (2)1+4a ;
(3)4b2+4b-1; (4)a2+ab+b2;
(5)x2+x+0.25.
是
(2)因为它只有两项;
不是
(3)4b 与-1的符号不统一;
不是
分析:
不是
是
(4)因为ab不是a与b的积的2倍.
(1)x2+12x+36
(2)4x2-4x+1
(3)(a+2b)2-2(a+2b)+1
典型例题
练习:将下列多项式分解因式:
(1)x2+12x+36=(x+6) 2
(2)4x2-4x+1=(2x-1) 2
(3)(a+2b) 2-2(a+2b)+1=(a+2b-1) 2
完全平方公式
平方差公式
公式法
分解因式
提公因式法
解:
(1)原式
= (2008-8)2
=20002
=4000000
利用分解因式解决问题
例2、利用简便方法计算:
(1)20082-2×2008×8+82
(2)4.321-+8.642×0.679+0.6792
解:
(2)原式
= 4.3212+2×4.321×0.679+0.6792
=(4.321+0.679)2
=25
典型例题
典型例题
综合方法分解因式
(2)-x2-4y2+4xy
例3、把下列各式分解因式:
(1)3ax2+6axy+3ay2
解:(1)原式
=3a(x2+2xy+y2)
= 3a(x+y)2
解:(2)原式
=-(x2+4y2-4xy)
=(x-2y)2
典型例题
(3)mx2-4m
解:(2)原式
=m(x2-4)
=m(x+2)(x-2)
一、先提公因式(有公因式)
二、平方差公式(剩余两项)
三、完全平方公式(剩余三项)
四、结果必须到不能分解为止
因式分解
建模分析
有一些是可以用整体的思想看成两项或三项
把下列各式分解因式:
典型例题
(1)x2+12xy+36y2
(2)16a4-8a2b2+b4
(3)-2xy-x2-y2
(4)4-12(x-y)+9(x-y)
(1)原式=(x+6y)2
(2)原式
=(4a2-b2)2=(2a+b)2(2a-b)2
(3)原式=-(x+y)2
(4)原式=(2-3x+3y)2
用平方差公式继续分解
3(x-y)=3x-3y
课堂小结
3.灵活应用分解因式的三种方法
2.会用完全平方式解决相关简算问题
1.牢记完全平方式的特征,:会用完全平方式分解因式
①三项 ②平方和 ③乘积2倍
紧扣完全平方式的特征,利用整体思想解决简算问题.
先考虑提公因式,剩余两项考虑平方差,剩余三项考虑完全平方.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.因式分解:
把一个多项式转化为几个整式的积的形式.
2.我们已经学过哪些因式分解的方法?
1.提公因式法
2.平方差公式
a2-b2=(a+b)(a-b)
导入新课
4.3 公式法(2)
学习目标
1.理解并掌握用完全平方公式分解因式.(重点)
2.灵活应用各种方法分解因式,并能利用因式分解进行计算.(难点)
用完全平方公式分解因式
一
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a
b
ab
讲授新课
这个大正方形的面积可以怎么求?
a2+2ab+b2
(a+b)2
=
a
b
a
b
a
ab
ab
b
(a+b)2
a2+2ab+b2
=
将上面的等式倒过来看,能得到:
a2+2ab+b2
a2-2ab+b2
我们把a +2ab+b 和a -2ab+b 这样的式子叫作完全平方式.
观察这两个式子:
(1)每个多项式有几项?
(3)中间项和第一项,第三项有什么关系?
(2)每个多项式的第一项和第三项有什么特征?
三项
这两项都是数或式的平方,并且符号相同
是第一项和第三项底数的积的±2倍
完全平方式的特点:
1.必须是三项式(或可以看成三项的);
2.有两个同号的数或式的平方;
3.中间有两底数之积的±2倍.
完全平方式:
简记口诀:
首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a ± b)
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
3.a +4ab+4b =( ) +2· ( ) ·( )+( ) =( )
2.m -6m+9=( ) - 2· ( ) ·( )+( ) =( )
1. x +4x+4= ( ) +2·( )·( )+( ) =( )
x
2
x + 2
a
a 2b
a + 2b
2b
对照 a ±2ab+b =(a±b) ,填空:
m
m - 3
3
x
2
m
3
下列各式是不是完全平方式?
(1)a2-4a+4; (2)1+4a ;
(3)4b2+4b-1; (4)a2+ab+b2;
(5)x2+x+0.25.
是
(2)因为它只有两项;
不是
(3)4b 与-1的符号不统一;
不是
分析:
不是
是
(4)因为ab不是a与b的积的2倍.
(1)x2+12x+36
(2)4x2-4x+1
(3)(a+2b)2-2(a+2b)+1
典型例题
练习:将下列多项式分解因式:
(1)x2+12x+36=(x+6) 2
(2)4x2-4x+1=(2x-1) 2
(3)(a+2b) 2-2(a+2b)+1=(a+2b-1) 2
完全平方公式
平方差公式
公式法
分解因式
提公因式法
解:
(1)原式
= (2008-8)2
=20002
=4000000
利用分解因式解决问题
例2、利用简便方法计算:
(1)20082-2×2008×8+82
(2)4.321-+8.642×0.679+0.6792
解:
(2)原式
= 4.3212+2×4.321×0.679+0.6792
=(4.321+0.679)2
=25
典型例题
典型例题
综合方法分解因式
(2)-x2-4y2+4xy
例3、把下列各式分解因式:
(1)3ax2+6axy+3ay2
解:(1)原式
=3a(x2+2xy+y2)
= 3a(x+y)2
解:(2)原式
=-(x2+4y2-4xy)
=(x-2y)2
典型例题
(3)mx2-4m
解:(2)原式
=m(x2-4)
=m(x+2)(x-2)
一、先提公因式(有公因式)
二、平方差公式(剩余两项)
三、完全平方公式(剩余三项)
四、结果必须到不能分解为止
因式分解
建模分析
有一些是可以用整体的思想看成两项或三项
把下列各式分解因式:
典型例题
(1)x2+12xy+36y2
(2)16a4-8a2b2+b4
(3)-2xy-x2-y2
(4)4-12(x-y)+9(x-y)
(1)原式=(x+6y)2
(2)原式
=(4a2-b2)2=(2a+b)2(2a-b)2
(3)原式=-(x+y)2
(4)原式=(2-3x+3y)2
用平方差公式继续分解
3(x-y)=3x-3y
课堂小结
3.灵活应用分解因式的三种方法
2.会用完全平方式解决相关简算问题
1.牢记完全平方式的特征,:会用完全平方式分解因式
①三项 ②平方和 ③乘积2倍
紧扣完全平方式的特征,利用整体思想解决简算问题.
先考虑提公因式,剩余两项考虑平方差,剩余三项考虑完全平方.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
