勾股定理
图片预览

文档简介
初二数学学案18.1.勾股定理(1)-证明 姓名_____ ____组____号
学习目标:1.经历勾股定理的探索过程,能熟记定理的内容
2.能运用勾股定理由直角三角形的已知两边求第三边
3.能运用勾股定理解一些简单的实际问题
学习过程:
一、知识回顾(用学过的知识完成下列填空)
①49的平方根是______ 算术平方根是_______
②已知Rt△ABC中的两条直角边长分别为a、b ,则S△ABC= 。
③已知梯形上下两底分别为a和b,高为(a+b),则该梯形的面积为 。
④完全平方公式:(a±b)2= 。
⑤在Rt△ABC中,已知∠A=30°,∠C=90°,直角边BC=1,则斜边AB= 。
二、自学交流
1.在我国古代,人们将直角三角形中_________叫做勾,_______叫做股,_______叫做弦.
2.(1)能发现各图中三个正方形的面积之间有何关系吗?
结论1:
(2)观察下面两幅图并填写右侧表格:
A的面积
B的面积
C的面积
左图
右图
(3)你是怎样得到正方形C的面积的?与同伴交流.
3.猜想命题:如果直角三角形的两条直角边分别为a、b,斜边为c,那么_________________
三、合作探究
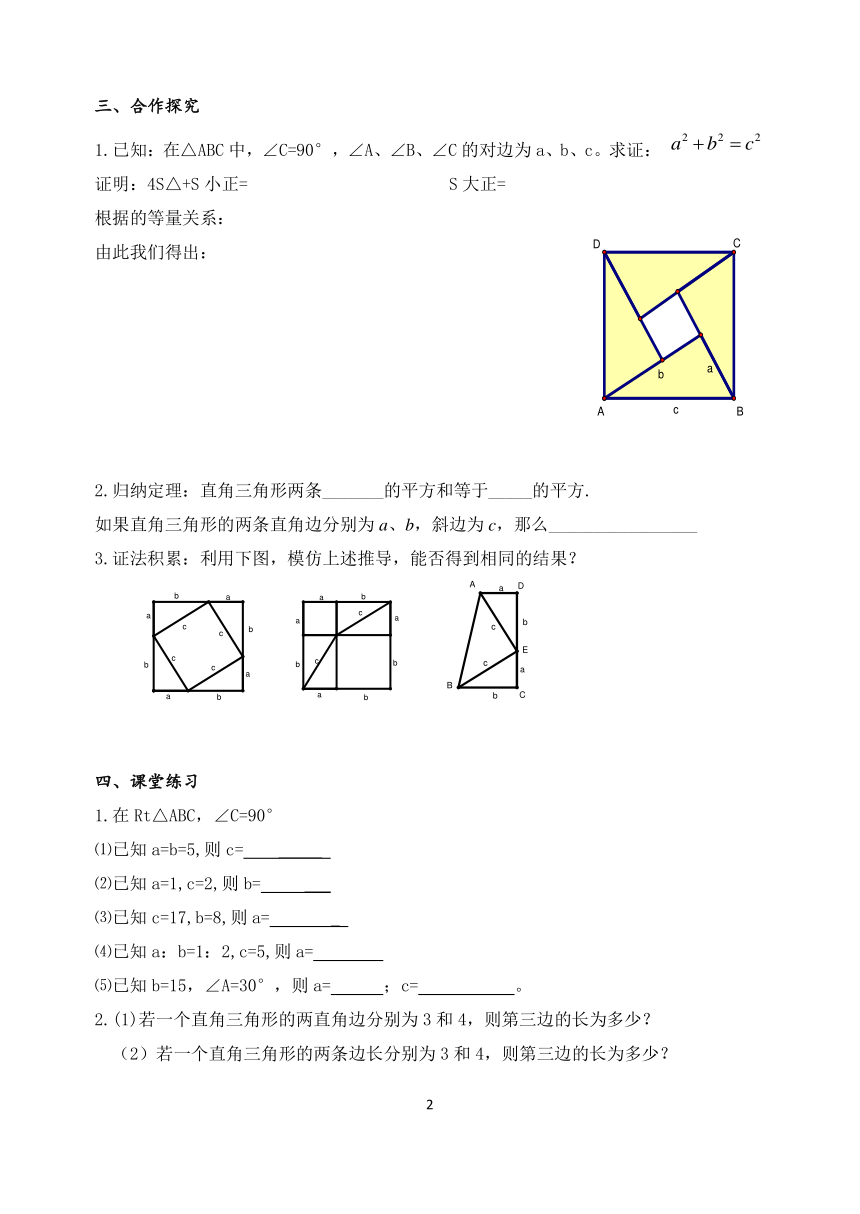
1.已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证: /
证明:4S△+S小正= S大正=
根据的等量关系:
由此我们得出:
2.归纳定理:直角三角形两条_______的平方和等于_____的平方.
如果直角三角形的两条直角边分别为a、b,斜边为c,那么_________________
3.证法积累:利用下图,模仿上述推导,能否得到相同的结果?
四、课堂练习
1.在Rt△ABC,∠C=90°
⑴已知a=b=5,则c= _____
⑵已知a=1,c=2,则b= ___
⑶已知c=17,b=8,则a= _
⑷已知a:b=1:2,c=5,则a=
⑸已知b=15,∠A=30°,则a= ;c= 。
2.(1)若一个直角三角形的两直角边分别为3和4,则第三边的长为多少?
(2)若一个直角三角形的两条边长分别为3和4,则第三边的长为多少?
3.已知:如图,等边△ABC的边长是6cm。
⑴求等边△ABC的高。 ⑵求S△ABC。
4.已知:如图,在△ABC中,∠C=60°,AB=/,AC=4,AD是BC边上的高,求BC的长。
五、当堂检测
1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;④若a∶b=3∶4,c=10则SRt△ABC=________。
2、一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为 。
3、一个直角三角形的两边长分别为5cm和12cm,则第三边的为 。
4、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为25 B.三角形周长为25 C.斜边长为5 D.三角形面积为20
5、已知,如图在ΔABC中,AB=BC=CA=2cm,AD是边BC上的高。
求 ①AD的长;②ΔABC的面积.
6、如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9。
(1)求DC的长。(2)求AB的长。
7、已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。
六、学习反馈
1、本节课都学习了什么内容?2、还有哪些不懂?3、应用勾股定理注意什么?
4、做错的题目有:
学习目标:1.经历勾股定理的探索过程,能熟记定理的内容
2.能运用勾股定理由直角三角形的已知两边求第三边
3.能运用勾股定理解一些简单的实际问题
学习过程:
一、知识回顾(用学过的知识完成下列填空)
①49的平方根是______ 算术平方根是_______
②已知Rt△ABC中的两条直角边长分别为a、b ,则S△ABC= 。
③已知梯形上下两底分别为a和b,高为(a+b),则该梯形的面积为 。
④完全平方公式:(a±b)2= 。
⑤在Rt△ABC中,已知∠A=30°,∠C=90°,直角边BC=1,则斜边AB= 。
二、自学交流
1.在我国古代,人们将直角三角形中_________叫做勾,_______叫做股,_______叫做弦.
2.(1)能发现各图中三个正方形的面积之间有何关系吗?
结论1:
(2)观察下面两幅图并填写右侧表格:
A的面积
B的面积
C的面积
左图
右图
(3)你是怎样得到正方形C的面积的?与同伴交流.
3.猜想命题:如果直角三角形的两条直角边分别为a、b,斜边为c,那么_________________
三、合作探究
1.已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。求证: /
证明:4S△+S小正= S大正=
根据的等量关系:
由此我们得出:
2.归纳定理:直角三角形两条_______的平方和等于_____的平方.
如果直角三角形的两条直角边分别为a、b,斜边为c,那么_________________
3.证法积累:利用下图,模仿上述推导,能否得到相同的结果?
四、课堂练习
1.在Rt△ABC,∠C=90°
⑴已知a=b=5,则c= _____
⑵已知a=1,c=2,则b= ___
⑶已知c=17,b=8,则a= _
⑷已知a:b=1:2,c=5,则a=
⑸已知b=15,∠A=30°,则a= ;c= 。
2.(1)若一个直角三角形的两直角边分别为3和4,则第三边的长为多少?
(2)若一个直角三角形的两条边长分别为3和4,则第三边的长为多少?
3.已知:如图,等边△ABC的边长是6cm。
⑴求等边△ABC的高。 ⑵求S△ABC。
4.已知:如图,在△ABC中,∠C=60°,AB=/,AC=4,AD是BC边上的高,求BC的长。
五、当堂检测
1、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;④若a∶b=3∶4,c=10则SRt△ABC=________。
2、一直角三角形的一直角边长为6,斜边长比另一直角边长大2,则斜边的长为 。
3、一个直角三角形的两边长分别为5cm和12cm,则第三边的为 。
4、一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )
A.斜边长为25 B.三角形周长为25 C.斜边长为5 D.三角形面积为20
5、已知,如图在ΔABC中,AB=BC=CA=2cm,AD是边BC上的高。
求 ①AD的长;②ΔABC的面积.
6、如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9。
(1)求DC的长。(2)求AB的长。
7、已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。
六、学习反馈
1、本节课都学习了什么内容?2、还有哪些不懂?3、应用勾股定理注意什么?
4、做错的题目有:
