分式同步练习作业
图片预览




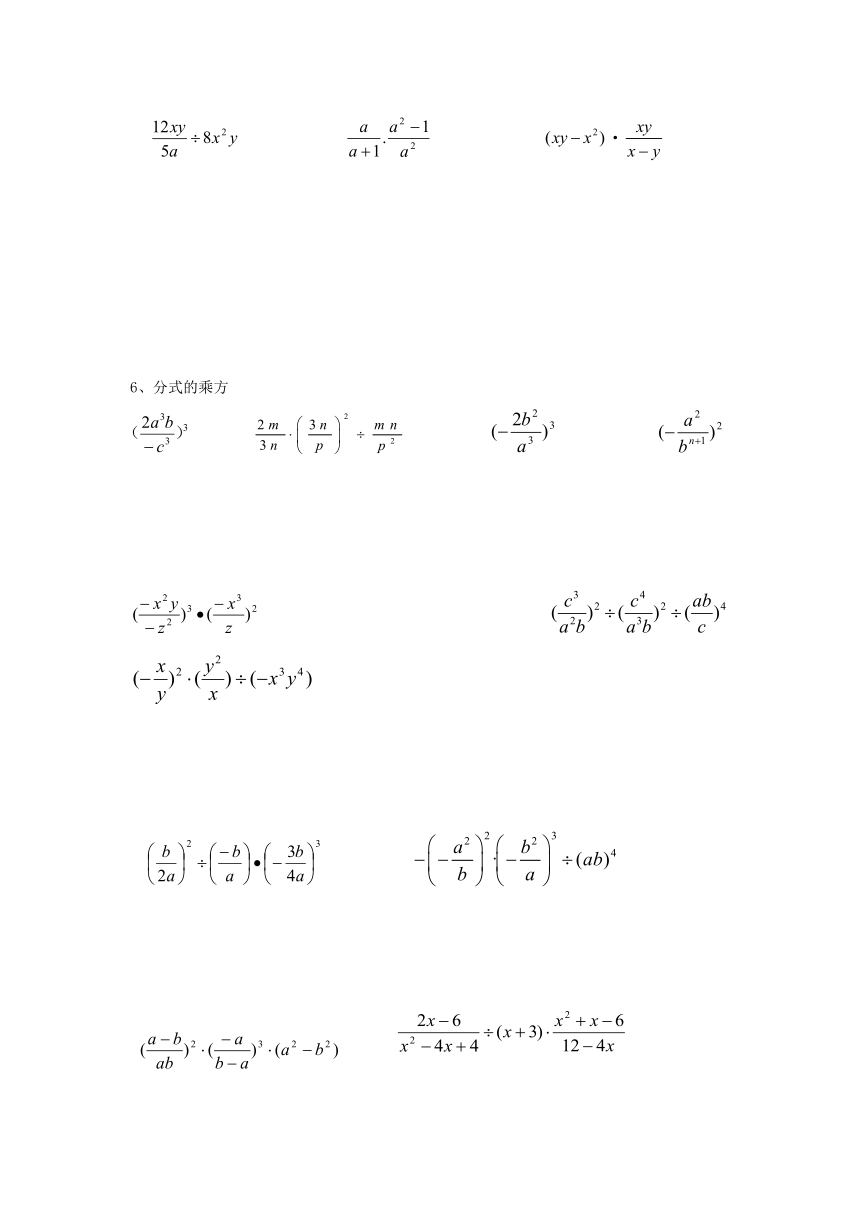
文档简介
作业1
一、分式概念及有关题型:
1.下列各式,, , 、、、、、
中,是分式的有
2.当x ________时,分式有意义, 当x______时,分式无意义,
3、当x _________时,分式的值为零。
4、当x为何值时,下列分式有意义.
(1) (2) (3)
5、当____时,分式的值为正;当____时,分式的值为负.
6、已知,则x ________
二.分式的基本性质
1、利用分式的基本性质填空:
(1) (2)
; (6)
(7) (8) ,
2、不改变分式的值,使分子、分母最高次项的系数为正数
3、不改变分式的值,把分子、分母的系数化为整数.
(1) (2)
4、把分式中的、都扩大3倍,那么分式的值( ) A、扩大3倍 B、不变 C、缩小3倍 D、缩小9倍
5、把分式中的、都扩大2倍,那么分式的值 ( ) A、扩大2倍 B、扩大4倍 C、缩小2倍 D不变
6、下列等式中成立的是 ( ) A、 B、 C、 D、
7、约分:
作业2
1、下列各式中,正确的是( )
A. B.=0 C. D.
2.无论x取什么数时,总是有意义的分式是( )
A. B. C. D.
3.下列判断中,正确的是( )
A.分式的分子中一定含有字母 B.当B=0时,分式无意义
C.当A=0时,分式的值为0(A、B为整式) D.分数一定是分式
4.下列各分式中,最简分式是( )
A. B. C. D.
5.若把分式中的x和y都扩大3倍,那么分式的值( )
A.扩大3倍 B.不变 C.缩小3倍 D.缩小6倍
6.若,则a是( ) A.正数 B.负数 C.零 D.任意有理数
7. 在,,,,+,9 x +,,中,分式的个数是( )
8.如果分式的值为为零,则a的值为( )
9.不改变分式的值,把分子、分母各项系数化为整数,结果为( )
10、对于分式,当x______时,分式无意义;当x______时,分式的值为0;
11.利用分式的基本性质填空:
,÷ = ; = _____
12.判断下列约分是否正确:
(1)= (2)= (3)=0
13.通分:(1),; (2),
14、通分 ,; , .
15先化简再求值 其中
16.已知 求的值
作业3
1、当x 时,分式无意义. 当x______时,分式有意义。
2、约分: ;= 。
3.通分:
4、化简求值 其中m=-1
5、分式的乘除运算
; ; 3xy2
·
6、分式的乘方
作业4
1.当x 时,分式有意义,若分式的值为0,则的取值为( )
2. 填空
3.计算: ; ;
-= .= ,= ;
4、用科学记数法表示:-0.0000000102= ;
5、各分式的最简公分母是____________
各分式的最简公分母为 。
6 计算:
(2×10-3)4÷(10-3)3 +-
++ -x-1.
7、先化简,再求值.
8、先化简,再求值: ,其中x=2
9、计算
(1)()÷. (2)
(3) (4)
(5) (6)
10、先化简,后求值:
,其中
作业5
a-b+
.
-.
三、先化简,再求值: ,其中.
-÷
作业6
1、下列方程中,是分式方程的是( )
① ②x+y=4, ③ ④
⑤ ⑥ ⑦ ⑧
2、解关于x分式方程:
(2)
(2) (4)
(5) (6)
9.某学校初二(1)班学生到游览区游览,游览区距学校24千米,男学生骑自行车,出发1小时20分钟后,女学生乘小客车出发,结果他们同时到达游览区,已知客车的速度是自行车的3倍,求自行车与客车的速度。
10、某一工程进行招标时,接到了甲、乙两个工程队的投标书,施工1天需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:
方案(1):甲工程队单独完成这项工程,刚好如期完成;
方案(2):乙工程队单独完成这项工程,要比规定日期多5天;
方案(3):若甲、乙两队合作4天,余下的工程由乙工程队单独做,也正好如期完成;
在不耽误工期的情况下,你觉得哪种方案最省钱?请说明理由。
11在抗震救灾活动中,某厂接到一份订单,要求生产7200顶帐篷支援四川灾区,后来由于情况紧急, 接收到上级指示,要求生产总量比原计划增加20%,且必须提前4天完成生产任务,该厂迅速加派人员组织生产,实际每天比原计划每天多生产720顶,请问该厂实际每天生产多少顶帐篷?
一、分式概念及有关题型:
1.下列各式,, , 、、、、、
中,是分式的有
2.当x ________时,分式有意义, 当x______时,分式无意义,
3、当x _________时,分式的值为零。
4、当x为何值时,下列分式有意义.
(1) (2) (3)
5、当____时,分式的值为正;当____时,分式的值为负.
6、已知,则x ________
二.分式的基本性质
1、利用分式的基本性质填空:
(1) (2)
; (6)
(7) (8) ,
2、不改变分式的值,使分子、分母最高次项的系数为正数
3、不改变分式的值,把分子、分母的系数化为整数.
(1) (2)
4、把分式中的、都扩大3倍,那么分式的值( ) A、扩大3倍 B、不变 C、缩小3倍 D、缩小9倍
5、把分式中的、都扩大2倍,那么分式的值 ( ) A、扩大2倍 B、扩大4倍 C、缩小2倍 D不变
6、下列等式中成立的是 ( ) A、 B、 C、 D、
7、约分:
作业2
1、下列各式中,正确的是( )
A. B.=0 C. D.
2.无论x取什么数时,总是有意义的分式是( )
A. B. C. D.
3.下列判断中,正确的是( )
A.分式的分子中一定含有字母 B.当B=0时,分式无意义
C.当A=0时,分式的值为0(A、B为整式) D.分数一定是分式
4.下列各分式中,最简分式是( )
A. B. C. D.
5.若把分式中的x和y都扩大3倍,那么分式的值( )
A.扩大3倍 B.不变 C.缩小3倍 D.缩小6倍
6.若,则a是( ) A.正数 B.负数 C.零 D.任意有理数
7. 在,,,,+,9 x +,,中,分式的个数是( )
8.如果分式的值为为零,则a的值为( )
9.不改变分式的值,把分子、分母各项系数化为整数,结果为( )
10、对于分式,当x______时,分式无意义;当x______时,分式的值为0;
11.利用分式的基本性质填空:
,÷ = ; = _____
12.判断下列约分是否正确:
(1)= (2)= (3)=0
13.通分:(1),; (2),
14、通分 ,; , .
15先化简再求值 其中
16.已知 求的值
作业3
1、当x 时,分式无意义. 当x______时,分式有意义。
2、约分: ;= 。
3.通分:
4、化简求值 其中m=-1
5、分式的乘除运算
; ; 3xy2
·
6、分式的乘方
作业4
1.当x 时,分式有意义,若分式的值为0,则的取值为( )
2. 填空
3.计算: ; ;
-= .= ,= ;
4、用科学记数法表示:-0.0000000102= ;
5、各分式的最简公分母是____________
各分式的最简公分母为 。
6 计算:
(2×10-3)4÷(10-3)3 +-
++ -x-1.
7、先化简,再求值.
8、先化简,再求值: ,其中x=2
9、计算
(1)()÷. (2)
(3) (4)
(5) (6)
10、先化简,后求值:
,其中
作业5
a-b+
.
-.
三、先化简,再求值: ,其中.
-÷
作业6
1、下列方程中,是分式方程的是( )
① ②x+y=4, ③ ④
⑤ ⑥ ⑦ ⑧
2、解关于x分式方程:
(2)
(2) (4)
(5) (6)
9.某学校初二(1)班学生到游览区游览,游览区距学校24千米,男学生骑自行车,出发1小时20分钟后,女学生乘小客车出发,结果他们同时到达游览区,已知客车的速度是自行车的3倍,求自行车与客车的速度。
10、某一工程进行招标时,接到了甲、乙两个工程队的投标书,施工1天需付甲工程队工程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:
方案(1):甲工程队单独完成这项工程,刚好如期完成;
方案(2):乙工程队单独完成这项工程,要比规定日期多5天;
方案(3):若甲、乙两队合作4天,余下的工程由乙工程队单独做,也正好如期完成;
在不耽误工期的情况下,你觉得哪种方案最省钱?请说明理由。
11在抗震救灾活动中,某厂接到一份订单,要求生产7200顶帐篷支援四川灾区,后来由于情况紧急, 接收到上级指示,要求生产总量比原计划增加20%,且必须提前4天完成生产任务,该厂迅速加派人员组织生产,实际每天比原计划每天多生产720顶,请问该厂实际每天生产多少顶帐篷?
