2021-2022学年度湘教版数学九年级上册课件 3.4.1.2 相似三角形的判定定理1(共20张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版数学九年级上册课件 3.4.1.2 相似三角形的判定定理1(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 22:23:18 | ||
图片预览






文档简介
(共20张PPT)
第3章
图形的相似
九年级数学湘教版·上册
3.4.1.2相似三角形的判定定理1
授课人:XXXX
教学目标
1.理解相似三角形的定义,掌握定义中的两个条件.
2.掌握相似三角形的判定定理1.(重点)
3.能熟练运用相似三角形的判定定理1.(难点)
新课导入
问题1 这两个三角形有什么关系?
观察与思考
全等三角形
新知探究
那这样变化一下呢?
新知探究
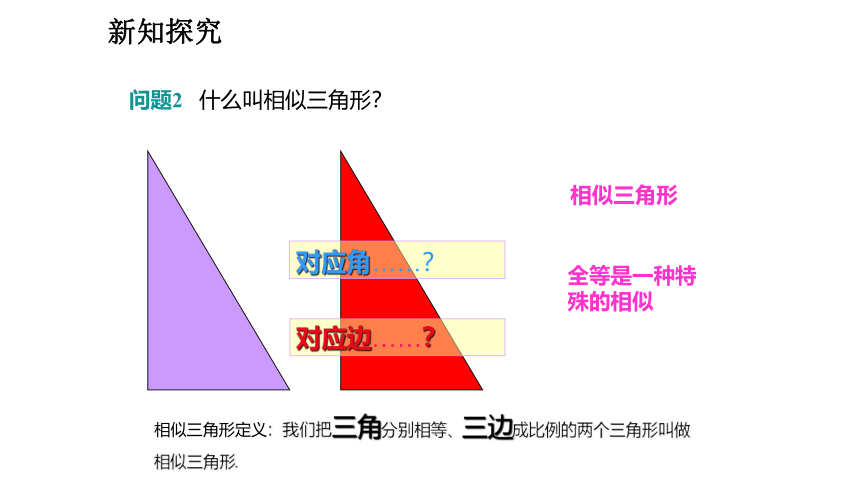
相似三角形
相似三角形定义:我们把三角分别相等、三边成比例的两个三角形叫做相似三角形.
对应角……?
对应边……?
问题2 什么叫相似三角形?
全等是一种特殊的相似
新知探究
定义 判定方法 全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等,三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边、直角边
H
L
问题3 三角形全等的性质和判定方法有哪些?
需要三个等量条件
思考 全等是一种特殊的相似,那你猜想一下,判定两个三角形相似需要几个条件?
新知探究
问题 观察学生与老师的直角三角板相似吗?测量一下,得出你的猜想.
利用角的关系判定两个三角形相似
新知探究
这两三角形是相似的
做一做:画△ABC,使∠A=30°,∠B=45°,再画△A′B′C′,使∠A′=30°,∠B′=45°.观察这两个三角形形状相同吗?你能证明∠C=∠C′吗?量出这两个三角形的三边,计算对应边是否对应成比例?由此你可以得出什么结论?
两角分别相等的两个三角形相似.
猜想:由以上的探究写出利用角判定两个三角形全等的条件.
探究猜想
新知探究
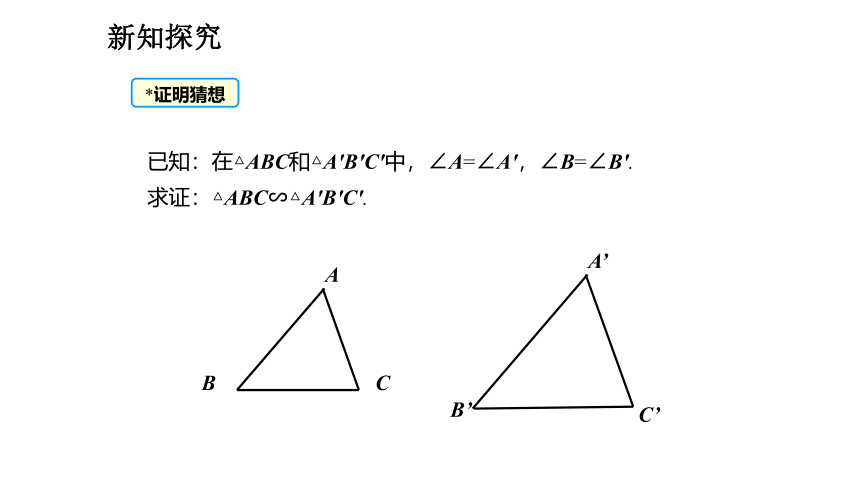
已知:在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′.
求证:△ABC∽△A′B′C′.
B’
A’
C’
B
A
C
*证明猜想
新知探究
证明:在△A′B′C′的边A′B′、A′C′上,分
别截取A′D=AB,A′E=AC,连接DE.
∵A′D=AB,∠A=∠A′,A′E=AC,
∴△A′DE≌△ABC,∴∠A′DE=∠B,
又∵∠B′=∠B,∴∠A′DE=∠B′,
∴DE∥B′C′,
∴△A′DE∽△A′B′C′,
∴△A′B′C′∽△ABC.
B'
A’
D
E
C'
B
A
C
知识归纳
两角分别相等的两个三角形相似.
归纳总结
A
B
C
A'
C'
B'
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形的判定定理1:
注意:对应点写在对应的位置.
新知探究
例1:如图,△ABC中,∠C=90°, 从点D分别作边AB,BC的垂线,垂足分别为点E,F,DF与AB交于点H.
求证:△DEH∽△BCA.
A
E
F
B
C
D
证明: ∵ ∠C= 90°, DF⊥BC,
∴∠BHF=∠A,
∴ △DEH∽△BCA.
(两角分别相等的两个三角形相似.)
H
∴ DF∥AC.
∴∠DHE=∠A,
∵ ∠DEH= 90°=∠C ,
新知探究
例2:如图,Rt△ABC与Rt△DEF中,∠C=∠F=90°, 若∠A=∠D, AB=5,BC=4,DE=3,求EF的长.
A
E
F
B
C
D
解: ∵ ∠C= ∠F=90°, ∠A=∠D,
∴ △ABC∽△DEF.
∵ AB=5,BC=4,DE=3,
∴ EF=2.4.
新知探究
例3:如图,△ABC中,DE∥BC,EF∥AB.
求证:△ADE∽△EFC.
A
E
F
B
C
D
解: ∵ DE∥BC,EF∥AB.
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
(两角分别相等的两个三角形相似.)
新知探究
例4:已知:如图,∠1=∠2=∠3,
求证:△ABC∽△ADE.
证明: ∵∠BAC= ∠1+ ∠DAC , ∠DAE= ∠3+ ∠DAC,
∵ ∠1=∠3,∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,∠E=180°-∠3-∠AOE.
又∵ ∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
在△ABC和△ ADE中 ∠BAC=∠DAE,∠C= ∠E
∴ △ABC∽△ADE.
课堂小结
利用两角判定三角形相似
定理1:两角分别相等的两个三角形相似
相似三角形的判定定理1的运用
课堂小测
1.已知:△ABC和△DEF中,∠A=40°,∠B=80 °,∠E=80 ° , ∠F=60 ° .求证:△ABC∽△DEF.
A
F
E
C
B
D
证明:∵ 在ΔABC中,∠A=40 ° ,∠B=80 ° ,
∴ ∠C=180 °-∠A-∠B=180 °-40 °-80 °=60 °.
∵ 在ΔDEF中,∠E=80 °,∠F=60 °.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC∽△DEF(两角对应相等,两三角形相似).
课堂小测
2.如图,在等边三角形ABC中,边长为10,点D在BC上,BD=6,∠ADE=60°,DE交AC于E.
(1)求证:△ABD∽△DCE;
∴∠BAD=∠CDE,∴△ABD∽△DCE.
证明:∵△ABC为等边三角形,
∴∠B=∠C=60°,∴∠ADB+∠BAD=120°,
又∠ADE=60°,∴∠ADB+∠CDE=120°,
课堂小测
(2)求CE的长.
6
10
4
解:∵ABD∽△DCE,
∴CE=2.4.
第3章
图形的相似
九年级数学湘教版·上册
3.4.1.2相似三角形的判定定理1
授课人:XXXX
教学目标
1.理解相似三角形的定义,掌握定义中的两个条件.
2.掌握相似三角形的判定定理1.(重点)
3.能熟练运用相似三角形的判定定理1.(难点)
新课导入
问题1 这两个三角形有什么关系?
观察与思考
全等三角形
新知探究
那这样变化一下呢?
新知探究
相似三角形
相似三角形定义:我们把三角分别相等、三边成比例的两个三角形叫做相似三角形.
对应角……?
对应边……?
问题2 什么叫相似三角形?
全等是一种特殊的相似
新知探究
定义 判定方法 全等三角形
相似三角形
三角、三边对应相等的两个三角形全等
三角对应相等,三边对应成比例的两个三角形相似
角边角
A
S
A
角角边
A
A
S
边边边
S
S
S
边角边
S
A
S
斜边、直角边
H
L
问题3 三角形全等的性质和判定方法有哪些?
需要三个等量条件
思考 全等是一种特殊的相似,那你猜想一下,判定两个三角形相似需要几个条件?
新知探究
问题 观察学生与老师的直角三角板相似吗?测量一下,得出你的猜想.
利用角的关系判定两个三角形相似
新知探究
这两三角形是相似的
做一做:画△ABC,使∠A=30°,∠B=45°,再画△A′B′C′,使∠A′=30°,∠B′=45°.观察这两个三角形形状相同吗?你能证明∠C=∠C′吗?量出这两个三角形的三边,计算对应边是否对应成比例?由此你可以得出什么结论?
两角分别相等的两个三角形相似.
猜想:由以上的探究写出利用角判定两个三角形全等的条件.
探究猜想
新知探究
已知:在△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′.
求证:△ABC∽△A′B′C′.
B’
A’
C’
B
A
C
*证明猜想
新知探究
证明:在△A′B′C′的边A′B′、A′C′上,分
别截取A′D=AB,A′E=AC,连接DE.
∵A′D=AB,∠A=∠A′,A′E=AC,
∴△A′DE≌△ABC,∴∠A′DE=∠B,
又∵∠B′=∠B,∴∠A′DE=∠B′,
∴DE∥B′C′,
∴△A′DE∽△A′B′C′,
∴△A′B′C′∽△ABC.
B'
A’
D
E
C'
B
A
C
知识归纳
两角分别相等的两个三角形相似.
归纳总结
A
B
C
A'
C'
B'
用数学符号表示:
∵ ∠A=∠A', ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形的判定定理1:
注意:对应点写在对应的位置.
新知探究
例1:如图,△ABC中,∠C=90°, 从点D分别作边AB,BC的垂线,垂足分别为点E,F,DF与AB交于点H.
求证:△DEH∽△BCA.
A
E
F
B
C
D
证明: ∵ ∠C= 90°, DF⊥BC,
∴∠BHF=∠A,
∴ △DEH∽△BCA.
(两角分别相等的两个三角形相似.)
H
∴ DF∥AC.
∴∠DHE=∠A,
∵ ∠DEH= 90°=∠C ,
新知探究
例2:如图,Rt△ABC与Rt△DEF中,∠C=∠F=90°, 若∠A=∠D, AB=5,BC=4,DE=3,求EF的长.
A
E
F
B
C
D
解: ∵ ∠C= ∠F=90°, ∠A=∠D,
∴ △ABC∽△DEF.
∵ AB=5,BC=4,DE=3,
∴ EF=2.4.
新知探究
例3:如图,△ABC中,DE∥BC,EF∥AB.
求证:△ADE∽△EFC.
A
E
F
B
C
D
解: ∵ DE∥BC,EF∥AB.
∴∠AED=∠C,
∠A=∠FEC.
∴ △ADE∽△EFC.
(两角分别相等的两个三角形相似.)
新知探究
例4:已知:如图,∠1=∠2=∠3,
求证:△ABC∽△ADE.
证明: ∵∠BAC= ∠1+ ∠DAC , ∠DAE= ∠3+ ∠DAC,
∵ ∠1=∠3,∴ ∠BAC=∠DAE.
∵ ∠C=180°-∠2-∠DOC ,∠E=180°-∠3-∠AOE.
又∵ ∠DOC =∠AOE(对顶角相等),
∴ ∠C= ∠E.
在△ABC和△ ADE中 ∠BAC=∠DAE,∠C= ∠E
∴ △ABC∽△ADE.
课堂小结
利用两角判定三角形相似
定理1:两角分别相等的两个三角形相似
相似三角形的判定定理1的运用
课堂小测
1.已知:△ABC和△DEF中,∠A=40°,∠B=80 °,∠E=80 ° , ∠F=60 ° .求证:△ABC∽△DEF.
A
F
E
C
B
D
证明:∵ 在ΔABC中,∠A=40 ° ,∠B=80 ° ,
∴ ∠C=180 °-∠A-∠B=180 °-40 °-80 °=60 °.
∵ 在ΔDEF中,∠E=80 °,∠F=60 °.
∴ ∠B=∠E,∠C=∠F.
∴ △ABC∽△DEF(两角对应相等,两三角形相似).
课堂小测
2.如图,在等边三角形ABC中,边长为10,点D在BC上,BD=6,∠ADE=60°,DE交AC于E.
(1)求证:△ABD∽△DCE;
∴∠BAD=∠CDE,∴△ABD∽△DCE.
证明:∵△ABC为等边三角形,
∴∠B=∠C=60°,∴∠ADB+∠BAD=120°,
又∠ADE=60°,∴∠ADB+∠CDE=120°,
课堂小测
(2)求CE的长.
6
10
4
解:∵ABD∽△DCE,
∴CE=2.4.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
