2021-2022学年度湘教版数学九年级上册 3.5相似三角形的应用 课件 (共30张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版数学九年级上册 3.5相似三角形的应用 课件 (共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 22:24:41 | ||
图片预览









文档简介
(共30张PPT)
第3章
图形的相似
九年级数学湘教版·上册
3.5相似三角形的应用
授课人:XXXX
教学目标
1.学会利用相似三角形解决高度(长度)测量问题.(重点、难点)
2.学会利用相似三角形解决河宽测量问题.(重点、难点)
新课导入
世界上最高的树
—— 红杉
新知探究
乐山大佛
新知探究
台北101大楼
新知探究
怎样测量这些非常高大物体的高度?
新知探究
世界上最宽的河
——亚马逊河
怎样测量河宽?
新知探究
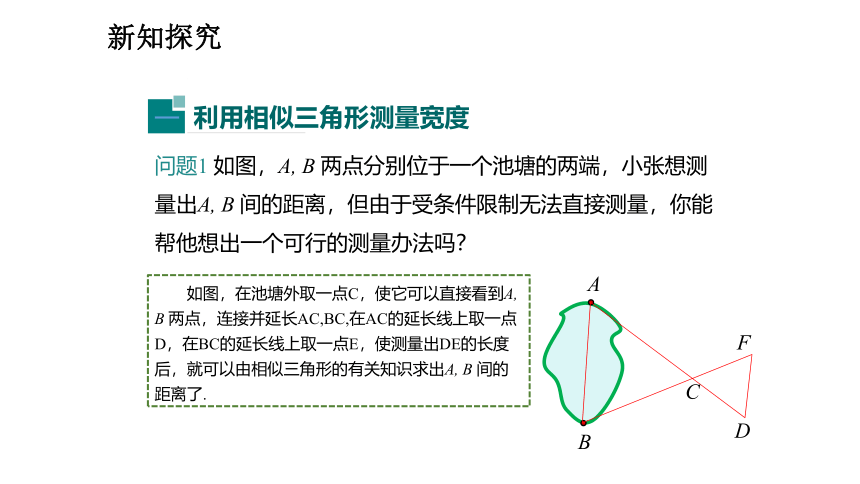
问题1 如图,A, B 两点分别位于一个池塘的两端,小张想测量出A, B 间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
利用相似三角形测量宽度
一
A
B
如图,在池塘外取一点C,使它可以直接看到A, B 两点,连接并延长AC,BC,在AC的延长线上取一点D,在BC的延长线上取一点E,使测量出DE的长度后,就可以由相似三角形的有关知识求出A, B 间的距离了.
C
D
F
新知探究
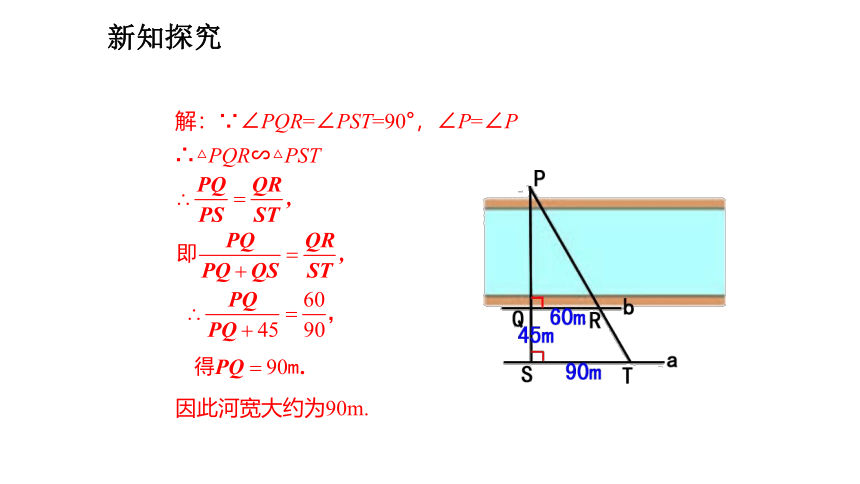
例1 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点为R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
新知探究
因此河宽大约为90m.
解:∵∠PQR=∠PST=90°,∠P=∠P
∴△PQR∽△PST
新知探究
测距的方法
测量不能到达两点间的距离,常构造相似三角形求解.
方法归纳
新知探究
问题2 胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度,你能根据图示说出他测量金字塔的原理吗?
运用相似三角形解决高度(长度)测量问题
二
新知探究
例2 如下图,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
我们来试着用学过的知识解决前面提出的问题.
新知探究
解:∵BF∥ED,∴∠BAO=∠EDF,
又∵∠AOB=∠DFE=90°,
∴△ABO∽△DEF,
∴ = ,∴ = ,
∴BO=134.
因此金字塔高134 m.
新知探究
物1高 :物2高 = 影1长 :影2长
测高方法1
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决.
新知探究
例3 在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图所示,在射击时,李明有轻微的抖动,致使准星A偏离到A′,若OA=0.2米,OB=50米,AA′=0.0005米,则李明射击到的点B′偏离目标点B的长度BB′.(近似地认为AA′ // BB′ )
新知探究
解:
答:李明射击到的点B′偏离目标点B的长度BB′为0.125m.
新知探究
例4 如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
分析:人、树、标杆是相互平行的,添加辅助线,过点A作AN∥BD交CD于N,交EF于M,则可得△AEM∽△ACN.
A
E
C
D
F
B
N
M
新知探究
A
E
C
D
F
B
N
解:过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°,
∴AB∥EF∥CD, ∴∠EMA=∠CNA.
∵∠EAM=∠CAN,
∴△AEM∽△ACN ,
∴ .
∵AB=1.6m , EF=2m , BD=27m , FD=24m ,
∴ , ∴CN=3.6m,
∴CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
M
新知探究
测高方法2:
测量不能到达顶部的物体的高度,也可以用“利用标杆测量高度”的原理解决.
新知探究
例5 为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
解:∵∠1=∠2,∠DCE=∠BAE=90°,
∴△DCE∽△BAE.
∴ ,
得 BA=18.75m.
因此,树高约为18.75m.
D
B
A
C
E
2
1
新知探究
测高方法3:
测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
新知探究
(1)根据题意画出___________;
(2)将题目中的已知量或已知关系转化为示意图中的
_____________________;
(3)利用相似三角形建立线段之间的关系,求出__________;
(4)写出___________.
示意图
已知线段、已知角
未知量
答案
利用三角形相似解决实际问题的一般步骤:
归纳总结
巩固练习
1.某同学想利用树影测量树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高多少米
E
D
6.4
1.2
?
1.5
1.4
A
B
c
解:作DE⊥AB于E
得
∴AE=8
∴AB=8+1.4=9.4(米).
物体的影长不等于地上的部分加上墙上的部分
课堂小结
相似三角形的应用
测量高度问题
测量河宽问题
课堂小测
1. 铁道口的栏杆短臂长1m,长臂长6m,当短臂端点下降0.5m时,长臂端点升高______m.
3
O
B
D
C
A
┏
┛
1m
6m
0.5m
?
2.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为______.
4米
课堂小测
3. 在△ABC和△A′B′C′中,已知:AB=6cm,
BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm.求证:△ABC与△A′B′C′相似.
证明:∵
∴
∴ △ABC ∽△A′B′C′
(三边成比例的两个三角形相似).
A
C
B
C′
A′
B′
课堂小测
4. 如图,某地四个乡镇建有公路,已知AB=14千米,AD=28千米, BD=21千米, BC=42千米,DC=31.5千米,公路AB与CD平行吗?说出你的理由.
解:公路AB与CD平行.
∵
14
28
21
42
31.5
A
B
C
D
∴ △ABD∽△BDC,
∴ ∠ABD=∠BDC
∴ AB∥DC
课堂小测
5.已知:如图,DE,DF,EF是△ABC的中位线.求证:△ABC∽△FED.
D
A
B
C
E
F
证明:
∵ DE,DF,EF是△ABC的中位线,
∴ DE= BC,DF= AC,EF= AB
∴ △ABC∽△FED
第3章
图形的相似
九年级数学湘教版·上册
3.5相似三角形的应用
授课人:XXXX
教学目标
1.学会利用相似三角形解决高度(长度)测量问题.(重点、难点)
2.学会利用相似三角形解决河宽测量问题.(重点、难点)
新课导入
世界上最高的树
—— 红杉
新知探究
乐山大佛
新知探究
台北101大楼
新知探究
怎样测量这些非常高大物体的高度?
新知探究
世界上最宽的河
——亚马逊河
怎样测量河宽?
新知探究
问题1 如图,A, B 两点分别位于一个池塘的两端,小张想测量出A, B 间的距离,但由于受条件限制无法直接测量,你能帮他想出一个可行的测量办法吗?
利用相似三角形测量宽度
一
A
B
如图,在池塘外取一点C,使它可以直接看到A, B 两点,连接并延长AC,BC,在AC的延长线上取一点D,在BC的延长线上取一点E,使测量出DE的长度后,就可以由相似三角形的有关知识求出A, B 间的距离了.
C
D
F
新知探究
例1 如图,为了估算河的宽度,我们可以在河对岸选定一个目标点P,在河的这一边取点Q和S,使点P、Q、S共线且直线PS与河垂直,接着在过点S且与PS垂直的直线a上选择适当的点T,确定PT与过点Q且垂直PS的直线b的交点为R.如果测得QS=45m,ST=90m,QR=60m,求河的宽度PQ.
新知探究
因此河宽大约为90m.
解:∵∠PQR=∠PST=90°,∠P=∠P
∴△PQR∽△PST
新知探究
测距的方法
测量不能到达两点间的距离,常构造相似三角形求解.
方法归纳
新知探究
问题2 胡夫金字塔是埃及现存规模最大的金字塔,被誉为“世界古代八大奇迹之一”,古希腊数学家,天文学家泰勒斯曾经利用相似三角形的原理测量金字塔的高度,你能根据图示说出他测量金字塔的原理吗?
运用相似三角形解决高度(长度)测量问题
二
新知探究
例2 如下图,如果木杆EF长2 m,它的影长FD为3 m,测得OA为201 m,求金字塔的高度BO.
我们来试着用学过的知识解决前面提出的问题.
新知探究
解:∵BF∥ED,∴∠BAO=∠EDF,
又∵∠AOB=∠DFE=90°,
∴△ABO∽△DEF,
∴ = ,∴ = ,
∴BO=134.
因此金字塔高134 m.
新知探究
物1高 :物2高 = 影1长 :影2长
测高方法1
测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成正比例”的原理解决.
新知探究
例3 在用枪瞄准目标点B时,要使眼睛O、准星A、目标B在同一条直线上,如图所示,在射击时,李明有轻微的抖动,致使准星A偏离到A′,若OA=0.2米,OB=50米,AA′=0.0005米,则李明射击到的点B′偏离目标点B的长度BB′.(近似地认为AA′ // BB′ )
新知探究
解:
答:李明射击到的点B′偏离目标点B的长度BB′为0.125m.
新知探究
例4 如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
分析:人、树、标杆是相互平行的,添加辅助线,过点A作AN∥BD交CD于N,交EF于M,则可得△AEM∽△ACN.
A
E
C
D
F
B
N
M
新知探究
A
E
C
D
F
B
N
解:过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
∴∠ABF=∠EFD=∠CDF=90°,
∴AB∥EF∥CD, ∴∠EMA=∠CNA.
∵∠EAM=∠CAN,
∴△AEM∽△ACN ,
∴ .
∵AB=1.6m , EF=2m , BD=27m , FD=24m ,
∴ , ∴CN=3.6m,
∴CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
M
新知探究
测高方法2:
测量不能到达顶部的物体的高度,也可以用“利用标杆测量高度”的原理解决.
新知探究
例5 为了测量一棵大树的高度,某同学利用手边的工具(镜子、皮尺)设计了如下测量方案:如图,
①在距离树AB底部15m的E处放下镜子;
②该同学站在距离镜子1.2m的C处,目高CD为1.5m;
③观察镜面,恰好看到树的顶端.
你能帮助他计算出大树的大约高度吗?
解:∵∠1=∠2,∠DCE=∠BAE=90°,
∴△DCE∽△BAE.
∴ ,
得 BA=18.75m.
因此,树高约为18.75m.
D
B
A
C
E
2
1
新知探究
测高方法3:
测量不能到达顶部的物体的高度,也可以用“利用镜子的反射测量高度”的原理解决.
新知探究
(1)根据题意画出___________;
(2)将题目中的已知量或已知关系转化为示意图中的
_____________________;
(3)利用相似三角形建立线段之间的关系,求出__________;
(4)写出___________.
示意图
已知线段、已知角
未知量
答案
利用三角形相似解决实际问题的一般步骤:
归纳总结
巩固练习
1.某同学想利用树影测量树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高多少米
E
D
6.4
1.2
?
1.5
1.4
A
B
c
解:作DE⊥AB于E
得
∴AE=8
∴AB=8+1.4=9.4(米).
物体的影长不等于地上的部分加上墙上的部分
课堂小结
相似三角形的应用
测量高度问题
测量河宽问题
课堂小测
1. 铁道口的栏杆短臂长1m,长臂长6m,当短臂端点下降0.5m时,长臂端点升高______m.
3
O
B
D
C
A
┏
┛
1m
6m
0.5m
?
2.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为______.
4米
课堂小测
3. 在△ABC和△A′B′C′中,已知:AB=6cm,
BC=8cm,AC=10cm,A′B′=18cm,B′C′=24cm,A′C′=30cm.求证:△ABC与△A′B′C′相似.
证明:∵
∴
∴ △ABC ∽△A′B′C′
(三边成比例的两个三角形相似).
A
C
B
C′
A′
B′
课堂小测
4. 如图,某地四个乡镇建有公路,已知AB=14千米,AD=28千米, BD=21千米, BC=42千米,DC=31.5千米,公路AB与CD平行吗?说出你的理由.
解:公路AB与CD平行.
∵
14
28
21
42
31.5
A
B
C
D
∴ △ABD∽△BDC,
∴ ∠ABD=∠BDC
∴ AB∥DC
课堂小测
5.已知:如图,DE,DF,EF是△ABC的中位线.求证:△ABC∽△FED.
D
A
B
C
E
F
证明:
∵ DE,DF,EF是△ABC的中位线,
∴ DE= BC,DF= AC,EF= AB
∴ △ABC∽△FED
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
