湖南省怀化市2013届高三上学期期末考试数学(文)试题
文档属性
| 名称 | 湖南省怀化市2013届高三上学期期末考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 336.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-01 18:27:07 | ||
图片预览



文档简介
湖南省怀化市2012-2013年高三期末考试数学(文)试题
本试卷分第一部分(选择题)和第二部分(非选择题)两部分,共150分. 时量:120分钟.
第一部分(选择题)
一、选择题:本大题共9小题,每小题5分,共计45分,在每小题给出的四个选项中,只有一项符合题目要求,请把正确答案的代号填在答题卡上.
1.下列命题是真命题的是
A.若,则 B.若,则
C.若,则 D.若,则
2.设复数满足(为虚数单位),则复数在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 设、,则“≥0”是“方程没有实数根”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知一个几何体的三视图如图所示,
则该几何体的体积是
A. B.
C. D.
5.已知,且
为幂函数,则的最大值为
A. B. C. D.
6.在上随机取一个数,则的概率为
A. B. C. D.
7.曲线在点处的切线方程是
A. B.
C. D.
8.函数的图象大致是
9.双曲线的渐近线都与圆相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程是
A. B. C. D.
第二部分(非选择题)
二、填空题:本大题共7小题,考生作答6小题,每小题5分,共30分. 把答案填在答题卡上的相应横线上.
(一)选作题(请考生在10、11两题中任选一题作答,如果全做,则按前一题记分)
10.在直角坐标系中,曲线的参数方程为(为参数).在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点,以轴为极轴)中,曲线的方程,与相交于两点,则公共弦的长是 .
11.已知某种生物药剂的最佳加入量在20g到30g之间.若
用0.618法安排试验,则第一次试点的加入量可以是 .
(二)必作题(12~16题)
12.观察下列等式:,,
,…, 照此规律,
计算 (N).
13.若某程序框图如图所示,则该程序运行后输出的值是 .
14.如图,已知正六边形的边长为2,
则= .
15.设集合,集合,
则 .
16.某企业生产甲、乙两种产品,已知生产每吨甲产品要用原料3吨,原料2吨;生产每吨乙产品要用原料1吨,原料3吨.销售每吨甲产品可获得利润4万元、每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗原料不超过13吨、原料不超过18吨,那么该企业可获得的最大利润是 .
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
在锐角中,分别是内角所对的边,且.
(1)求角的大小;
(2)若,且,求的面积.
18.(本小题满分12分)
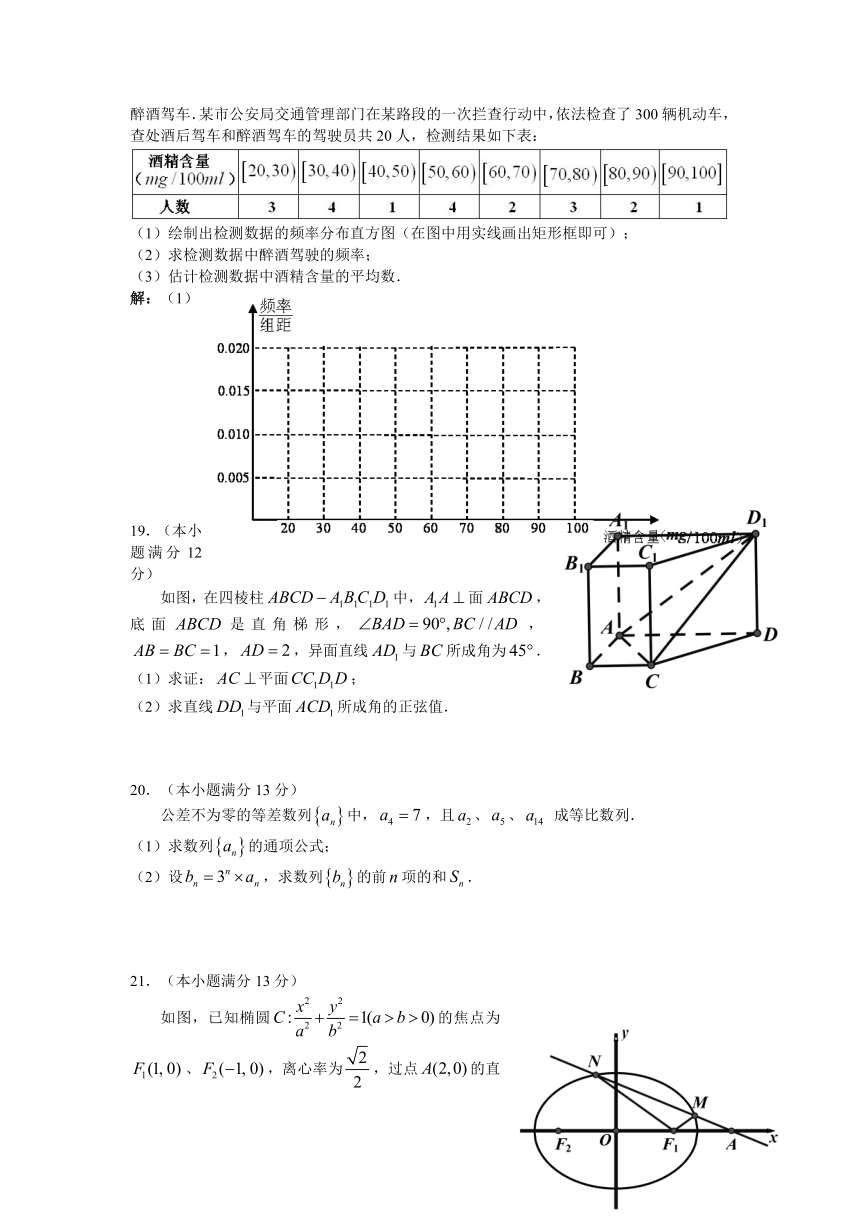
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在+~(不含80)之间,属于酒后驾车;在(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
(1)绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);
(2)求检测数据中醉酒驾驶的频率;
(3)估计检测数据中酒精含量的平均数.
解:(1)
19.(本小题满分12分)
如图,在四棱柱中,面,底面是直角梯形,,,,异面直线与所成角为.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
20.(本小题满分13分)
公差不为零的等差数列中,,且、、 成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前项的和.
21.(本小题满分13分)
如图,已知椭圆的焦点为、,离心率为,过点的直线交椭圆于、两点.
(1)求椭圆的方程;
(2)①求直线的斜率的取值范围;
②在直线的斜率不断变化过程中,探究和是否总相等?若相等,请给出证明,若不相等,说明理由.
22.(本小题满分13分)
已知R,函数.
(1)求的单调区间;
(2)证明:当时,.
2012年下学期期末教学质量统一检测试卷
高三数学(文科)参考答案与评分标准
一、选择题()
题号
1
2
3
4
5
6
7
8
9
答案
C
D
B
A
A
D
B
C
B
二、填空题()
10.; 11.26.18或23.82(写出一个记满分); 12.; 13.38; 14.; 15.; 16.24万元.
三、解答题:
17解:(1)由正弦定理,得……………2分
因为,所以,又角为锐角,故…………5分
(2)由(1)知,且,由余弦定理,得:
………………………7分
即,由,得,
则有或 …………………………10分
所以,的面积…………………12分
18解:(1)检测数据的频率分布直方图如下:(4分)
(2)所求频率为 ………………8分
(3)估计所求平均数为
……………12分
19解:(1)由已知得,底面,平面,
所以 ……………2分
又,,,
所以,
所以 …………4分
又,故平面 …………6分
(2)因为,所以为异面直线与所成角,即为,
又,所以 ……………8分
过点作,为垂足,由(1)知,,又,
所以平面,
故是直线与平面所成角,记为 …………10分
在中,,
所以 …………12分
(2)另解:因为,所以为异面直线与所成角,即为,
又,所以 ……………8分
设点到平面的距离为,直线与平面所成角为,
又由(1)知,,,
由等体积法得:,
即,解得 ………10分
所以 …………12分
20解:(1)设公差为,则解得……4分
所以数列的通项公式为 ………6分
(2)由(1)可知,,则
①
②
由①—②得: ………9分
………11分
所以, ………13分
21解:(1)由已知条件知,,得,又,
所以椭圆的方程为 …………4分
(2)直线的方程为,
联立,得 ………6分
由于直线与椭圆相交,所以,
解得直线的斜率的取值范围是 ………8分
②和总相等.证明:设,则
…………9分
所以
………11分
所以 ………13分
22解:(1)由题意得 ………2分
当时,恒成立,此时的单调区间为 ……4分
当时,,
此时的单调递增区间为和,
单调递减区间为 ……………6分
(2)证明:由于,所以当时,
…………8分
当时,……10分
设,则,
于是随的变化情况如下表:
0
1
0
1
减
极小值
增
1
所以, …………12分
所以,当时,,
故 …………13分
(2)另解:由于,所以当时,.
令,则.
当时,在上递增, ………8分
当时,,在上递减,在上递增,所以.
故当时, ………10分
当时,.
设,则,
③当时,在上递减, ……11分
④当时,在上递减,在上递增,所以
.
故当时,.
故 …………13分
本试卷分第一部分(选择题)和第二部分(非选择题)两部分,共150分. 时量:120分钟.
第一部分(选择题)
一、选择题:本大题共9小题,每小题5分,共计45分,在每小题给出的四个选项中,只有一项符合题目要求,请把正确答案的代号填在答题卡上.
1.下列命题是真命题的是
A.若,则 B.若,则
C.若,则 D.若,则
2.设复数满足(为虚数单位),则复数在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 设、,则“≥0”是“方程没有实数根”的
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知一个几何体的三视图如图所示,
则该几何体的体积是
A. B.
C. D.
5.已知,且
为幂函数,则的最大值为
A. B. C. D.
6.在上随机取一个数,则的概率为
A. B. C. D.
7.曲线在点处的切线方程是
A. B.
C. D.
8.函数的图象大致是
9.双曲线的渐近线都与圆相切,且双曲线的右焦点为圆C的圆心,则该双曲线的方程是
A. B. C. D.
第二部分(非选择题)
二、填空题:本大题共7小题,考生作答6小题,每小题5分,共30分. 把答案填在答题卡上的相应横线上.
(一)选作题(请考生在10、11两题中任选一题作答,如果全做,则按前一题记分)
10.在直角坐标系中,曲线的参数方程为(为参数).在极坐标系(与直角坐标系取相同的长度单位,且以原点为极点,以轴为极轴)中,曲线的方程,与相交于两点,则公共弦的长是 .
11.已知某种生物药剂的最佳加入量在20g到30g之间.若
用0.618法安排试验,则第一次试点的加入量可以是 .
(二)必作题(12~16题)
12.观察下列等式:,,
,…, 照此规律,
计算 (N).
13.若某程序框图如图所示,则该程序运行后输出的值是 .
14.如图,已知正六边形的边长为2,
则= .
15.设集合,集合,
则 .
16.某企业生产甲、乙两种产品,已知生产每吨甲产品要用原料3吨,原料2吨;生产每吨乙产品要用原料1吨,原料3吨.销售每吨甲产品可获得利润4万元、每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗原料不超过13吨、原料不超过18吨,那么该企业可获得的最大利润是 .
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
在锐角中,分别是内角所对的边,且.
(1)求角的大小;
(2)若,且,求的面积.
18.(本小题满分12分)
《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在+~(不含80)之间,属于酒后驾车;在(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
(1)绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);
(2)求检测数据中醉酒驾驶的频率;
(3)估计检测数据中酒精含量的平均数.
解:(1)
19.(本小题满分12分)
如图,在四棱柱中,面,底面是直角梯形,,,,异面直线与所成角为.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
20.(本小题满分13分)
公差不为零的等差数列中,,且、、 成等比数列.
(1)求数列的通项公式;
(2)设,求数列的前项的和.
21.(本小题满分13分)
如图,已知椭圆的焦点为、,离心率为,过点的直线交椭圆于、两点.
(1)求椭圆的方程;
(2)①求直线的斜率的取值范围;
②在直线的斜率不断变化过程中,探究和是否总相等?若相等,请给出证明,若不相等,说明理由.
22.(本小题满分13分)
已知R,函数.
(1)求的单调区间;
(2)证明:当时,.
2012年下学期期末教学质量统一检测试卷
高三数学(文科)参考答案与评分标准
一、选择题()
题号
1
2
3
4
5
6
7
8
9
答案
C
D
B
A
A
D
B
C
B
二、填空题()
10.; 11.26.18或23.82(写出一个记满分); 12.; 13.38; 14.; 15.; 16.24万元.
三、解答题:
17解:(1)由正弦定理,得……………2分
因为,所以,又角为锐角,故…………5分
(2)由(1)知,且,由余弦定理,得:
………………………7分
即,由,得,
则有或 …………………………10分
所以,的面积…………………12分
18解:(1)检测数据的频率分布直方图如下:(4分)
(2)所求频率为 ………………8分
(3)估计所求平均数为
……………12分
19解:(1)由已知得,底面,平面,
所以 ……………2分
又,,,
所以,
所以 …………4分
又,故平面 …………6分
(2)因为,所以为异面直线与所成角,即为,
又,所以 ……………8分
过点作,为垂足,由(1)知,,又,
所以平面,
故是直线与平面所成角,记为 …………10分
在中,,
所以 …………12分
(2)另解:因为,所以为异面直线与所成角,即为,
又,所以 ……………8分
设点到平面的距离为,直线与平面所成角为,
又由(1)知,,,
由等体积法得:,
即,解得 ………10分
所以 …………12分
20解:(1)设公差为,则解得……4分
所以数列的通项公式为 ………6分
(2)由(1)可知,,则
①
②
由①—②得: ………9分
………11分
所以, ………13分
21解:(1)由已知条件知,,得,又,
所以椭圆的方程为 …………4分
(2)直线的方程为,
联立,得 ………6分
由于直线与椭圆相交,所以,
解得直线的斜率的取值范围是 ………8分
②和总相等.证明:设,则
…………9分
所以
………11分
所以 ………13分
22解:(1)由题意得 ………2分
当时,恒成立,此时的单调区间为 ……4分
当时,,
此时的单调递增区间为和,
单调递减区间为 ……………6分
(2)证明:由于,所以当时,
…………8分
当时,……10分
设,则,
于是随的变化情况如下表:
0
1
0
1
减
极小值
增
1
所以, …………12分
所以,当时,,
故 …………13分
(2)另解:由于,所以当时,.
令,则.
当时,在上递增, ………8分
当时,,在上递减,在上递增,所以.
故当时, ………10分
当时,.
设,则,
③当时,在上递减, ……11分
④当时,在上递减,在上递增,所以
.
故当时,.
故 …………13分
同课章节目录
