10.3 平行线的性质(18) 课件(共21张PPT)
文档属性
| 名称 | 10.3 平行线的性质(18) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 404.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 10:07:38 | ||
图片预览



文档简介
(共21张PPT)
10.3 平行线的性质
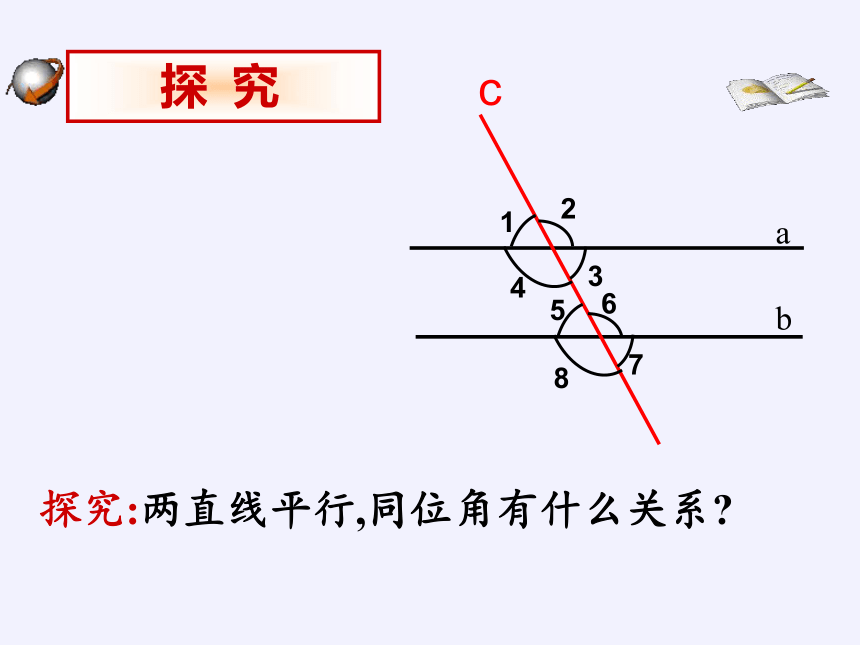
探究:两直线平行,同位角有什么关系
a
b
探 究
c
1
5
2
3
4
7
6
8
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
65°
65°
c
a
b
1
5
2
4
3
6
8
7
∠1=∠5
a∥b
请你动动手
简单地说:两直线平行,同位角相等.
a
b
1
2
3
4
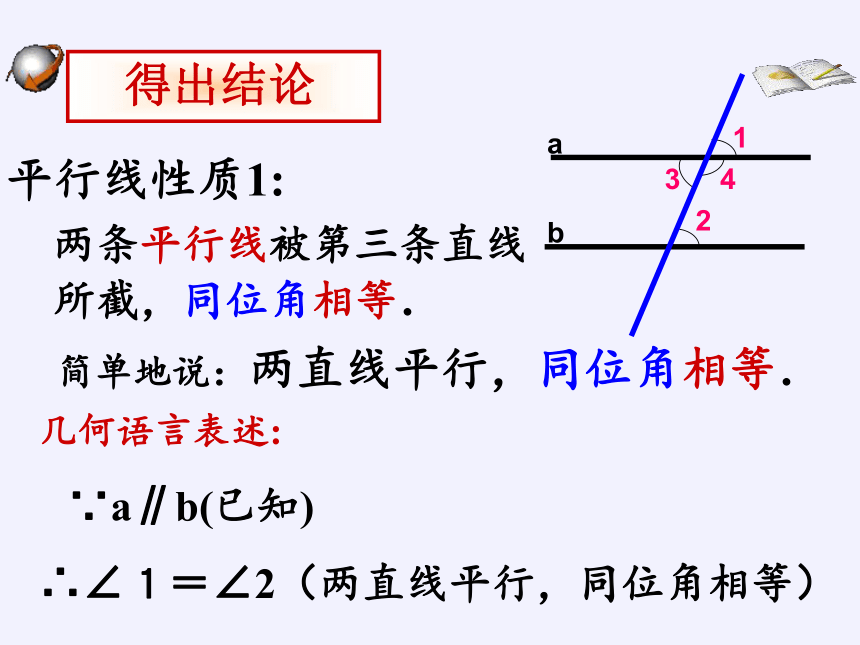
得出结论
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
两条平行线被第三条直线所截,同位角相等.
平行线性质1:
两直线平行,同位角相等.
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
a
b
1
2
3
4
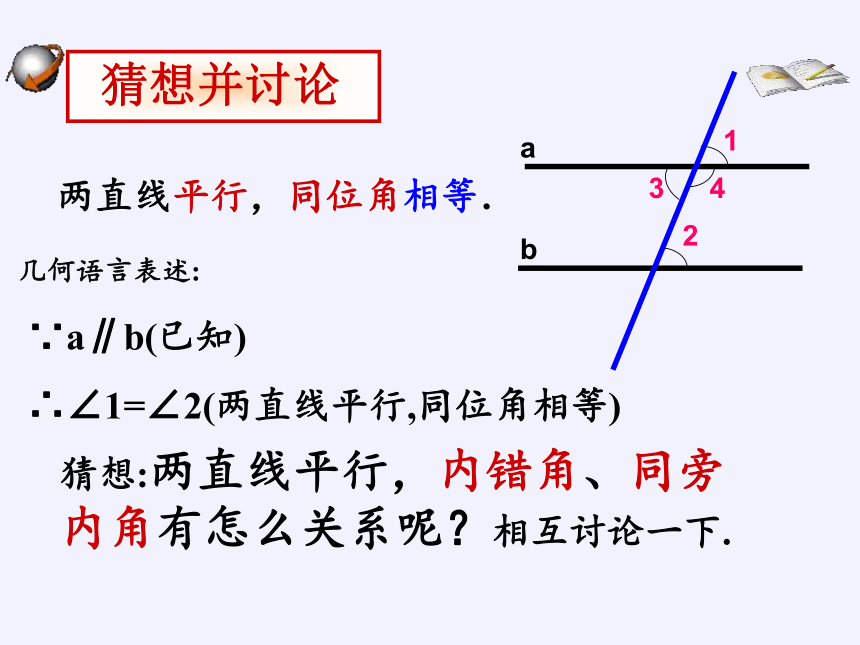
猜想并讨论
猜想:两直线平行,内错角、同旁内角有怎么关系呢?相互讨论一下.
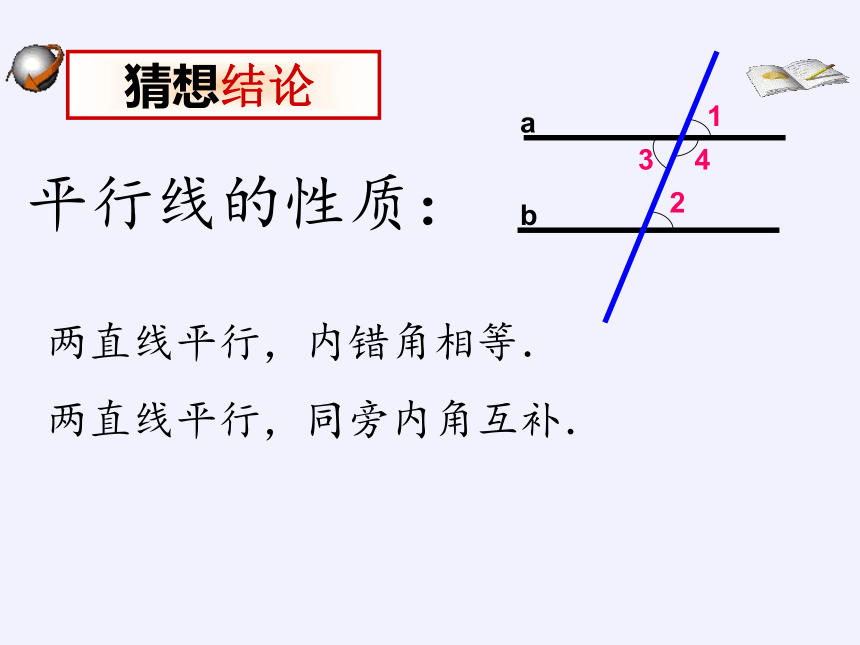
两直线平行,内错角相等.
两直线平行,同旁内角互补.
平行线的性质:
a
b
1
2
3
4
猜想结论
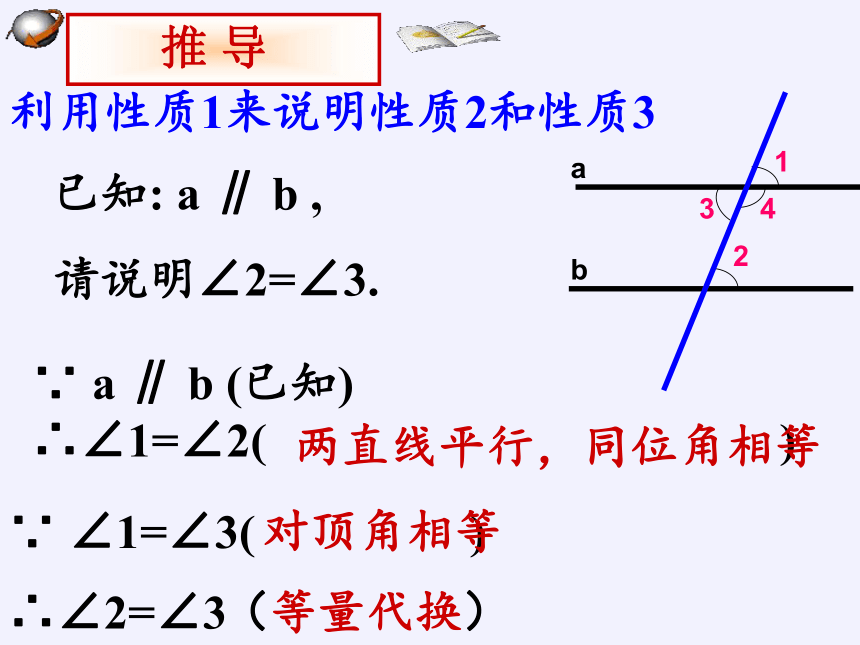
利用性质1来说明性质2和性质3
a
b
1
2
3
4
已知: a ∥ b ,
请说明∠2=∠3.
∵ a ∥ b (已知)
∴∠1=∠2( )
∵ ∠1=∠3( )
∴∠2=∠3
两直线平行,同位角相等
对顶角相等
(等量代换)
推 导
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:
两条平行线被第三条直线所截,
a
b
1
2
3
4
得出结论
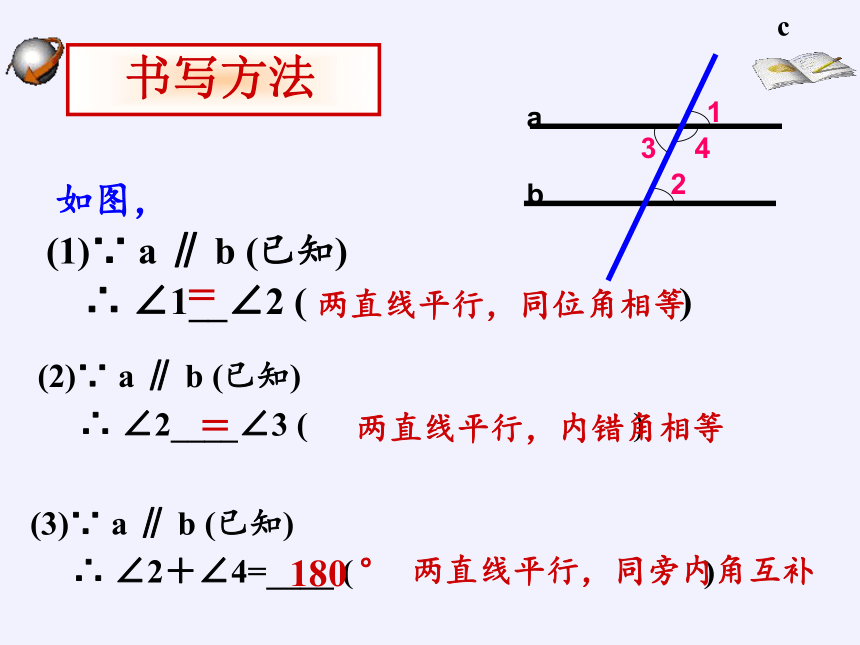
如图,
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 ( )
(3)∵ a ∥ b (已知)
∴ ∠2+∠4=____ ( )
=
两直线平行,同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
c
a
b
1
2
3
4
书写方法
例题讲解
例 如图10-18,已知点D,E,F分别△ABC的边AB,AC,BC上,且DE∥BC,∠B=48 .
(1)试求∠ADE的度数;
(2)如果∠DEF=48 ,那么EF与AB平行吗?
解(1)∵DE∥BC(已知)
∴∠ADE=∠B=48 (两直线平行, 同位角相等)
(2)由(1)得∠ADE=48
又∵∠DEF=48
∴EF∥AB(内错角相等,两直线平行)
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度 为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
一、快速抢答
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行,内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、快速抢答
2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
B
C
∠C=142o
∵两直线平行,内错角相等
一、快速抢答
3、如图直线 a ∥ b,直线b垂直于直线c,则直线a垂直于直线c吗
∟
∟
a
b
c
a⊥c
∵两直线平行, 同位角相等
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
图形
已知
结果
理由
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
小结
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
布置作业:
作业:P131 第4题
谢谢聆听!
例 如图所示是一块梯形铁片的残余部分,量得∠A=100 , ∠B=115°,梯形另外两个角各是多少度?
解决问题:
1、如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度
解:
∵ ∠2=∠1 (对顶角相等)
∴ ∠2=∠1 =54°
∵ a∥b(已知)
∴ ∠4=∠1=54°(两直线平行,同位角相等)
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
即 ∠2=54° ,∠3=126°, ∠4=54°。
1
2
3
4
a
b
你会做吗?
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
2、已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
证:(1)DE∥BC
(2) ∠C的度数
谢 谢
10.3 平行线的性质
探究:两直线平行,同位角有什么关系
a
b
探 究
c
1
5
2
3
4
7
6
8
如图,直线a∥b,
(1)测量同位角∠1和∠5的大小,它们有什么关系?
65°
65°
c
a
b
1
5
2
4
3
6
8
7
∠1=∠5
a∥b
请你动动手
简单地说:两直线平行,同位角相等.
a
b
1
2
3
4
得出结论
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
两条平行线被第三条直线所截,同位角相等.
平行线性质1:
两直线平行,同位角相等.
几何语言表述:
∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)
a
b
1
2
3
4
猜想并讨论
猜想:两直线平行,内错角、同旁内角有怎么关系呢?相互讨论一下.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
平行线的性质:
a
b
1
2
3
4
猜想结论
利用性质1来说明性质2和性质3
a
b
1
2
3
4
已知: a ∥ b ,
请说明∠2=∠3.
∵ a ∥ b (已知)
∴∠1=∠2( )
∵ ∠1=∠3( )
∴∠2=∠3
两直线平行,同位角相等
对顶角相等
(等量代换)
推 导
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:
两条平行线被第三条直线所截,
a
b
1
2
3
4
得出结论
如图,
(1)∵ a ∥ b (已知)
∴ ∠1__∠2 ( )
(2)∵ a ∥ b (已知)
∴ ∠2____∠3 ( )
(3)∵ a ∥ b (已知)
∴ ∠2+∠4=____ ( )
=
两直线平行,同位角相等
=
两直线平行,内错角相等
180 °
两直线平行,同旁内角互补
c
a
b
1
2
3
4
书写方法
例题讲解
例 如图10-18,已知点D,E,F分别△ABC的边AB,AC,BC上,且DE∥BC,∠B=48 .
(1)试求∠ADE的度数;
(2)如果∠DEF=48 ,那么EF与AB平行吗?
解(1)∵DE∥BC(已知)
∴∠ADE=∠B=48 (两直线平行, 同位角相等)
(2)由(1)得∠ADE=48
又∵∠DEF=48
∴EF∥AB(内错角相等,两直线平行)
1、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110o可以知道∠2 是多少度 为什么?
(2)从∠1=110o可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110 o可以知道∠4 是多少度?为什么?
一、快速抢答
2
E
1
3
4
A
B
D
C
∠2=110o
∵两直线行,内错角相等
∠3=110o
∵两直线平行,同位角相等
∠4=70o
∵两直线平行,同旁内角互补
一、快速抢答
2、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
B
C
∠C=142o
∵两直线平行,内错角相等
一、快速抢答
3、如图直线 a ∥ b,直线b垂直于直线c,则直线a垂直于直线c吗
∟
∟
a
b
c
a⊥c
∵两直线平行, 同位角相等
同位角相等
内错角相等
同旁内角互补
两直线平行
判定
性质
已知
得到
得到
已知
小结:
图形
已知
结果
理由
同位角
内错角
同旁内角
两直线平行
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
小结
a//b
两直线平行
同位角相等
a//b
两直线平行
内错角相等
a//b
布置作业:
作业:P131 第4题
谢谢聆听!
例 如图所示是一块梯形铁片的残余部分,量得∠A=100 , ∠B=115°,梯形另外两个角各是多少度?
解决问题:
1、如图,直线a∥b, ∠1=54°,∠2, ∠3, ∠4各是多少度
解:
∵ ∠2=∠1 (对顶角相等)
∴ ∠2=∠1 =54°
∵ a∥b(已知)
∴ ∠4=∠1=54°(两直线平行,同位角相等)
∠2+∠3=180°(两直线平行,同旁内角互补)
∴ ∠3= 180°- ∠2= 180° - 54°=126°
即 ∠2=54° ,∠3=126°, ∠4=54°。
1
2
3
4
a
b
你会做吗?
(已知)
(1)∵∠ADE=60 ° ∠B=60 °
∴∠ADE=∠B
(等量代换)
∴DE∥BC
(同位角相等,两直线平行)
(2)∵ DE∥BC
(已证)
∴∠AED=∠C
(两直线平行,同位角相等)
又∵∠AED=40°
(已知)
(等量代换)
∴∠C=40 °
2、已知 ∠ADE=60 ° ∠B=60 °∠AED=40°
证:(1)DE∥BC
(2) ∠C的度数
谢 谢
