沪科版数学七年级下册 10.3 平行线的性质 课件(共20张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.3 平行线的性质 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 494.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 11:36:29 | ||
图片预览






文档简介
(共20张PPT)
10.3 平行线的性质
数学不是看出来的,也不是单纯想出来的,更重要的是做出来的。
世界著名的意大利比萨斜塔,建于公元1173年,为8层圆柱形建筑,全部用白色大理石砌成,塔高54.5米.
创设情境,复习导入
它与地面所
成的较大的
角是多少度
目前,它与地面所成较小的角
为∠1=85
1
2
3
复习回顾 根据右图,填空:
①如果∠1=∠2,
那么__∥__( )
② 如果∠3=∠2
那么__∥__( )
③ 如果∠3+∠4=180°,
那么__∥__( )
同位角相等
内错角相等
同旁内角互补
两直线平行
AB
CD
AB
CD
同位角相等,两直线平行
内错角相等,两直线平行
AB
CD
同旁内角互补,两直线平行
1
2
3
4
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
10.3平行线的性质
a
b
c
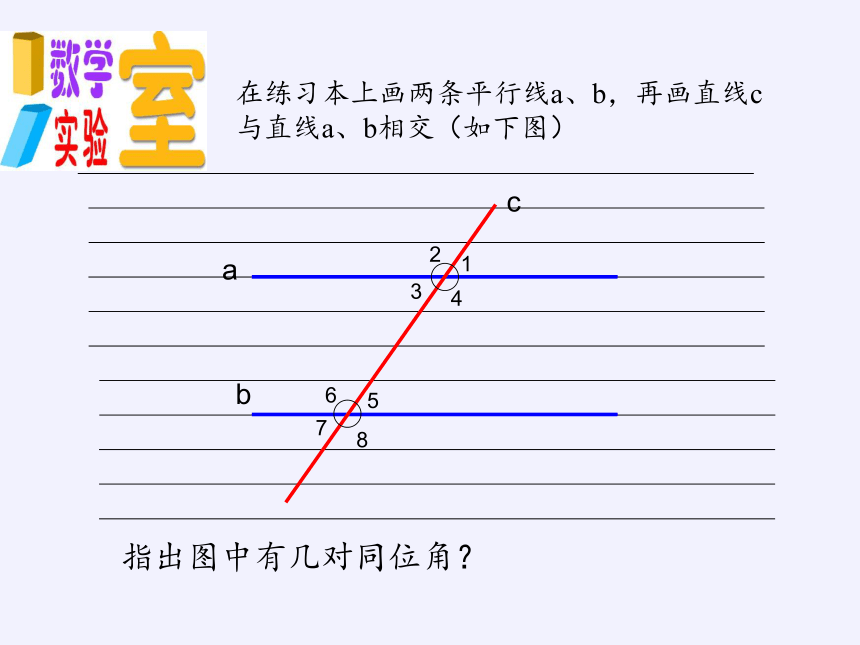
在练习本上画两条平行线a、b,再画直线c与直线a、b相交(如下图)
指出图中有几对同位角?
3
4
1
5
2
6
8
7
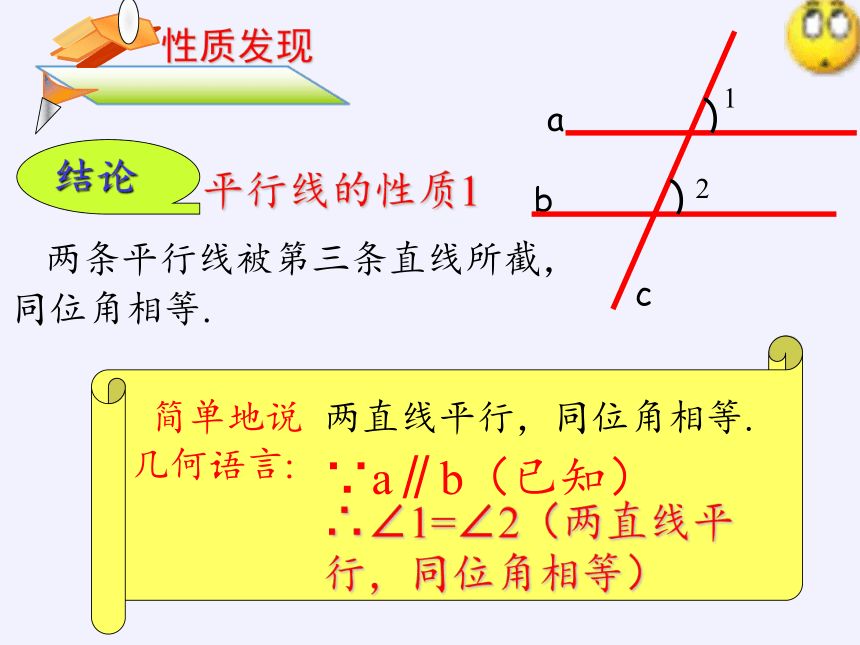
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2(两直线平 行,同位角相等)
∵a∥b(已知)
简单地说:
几何语言:
b
1
2
a
c
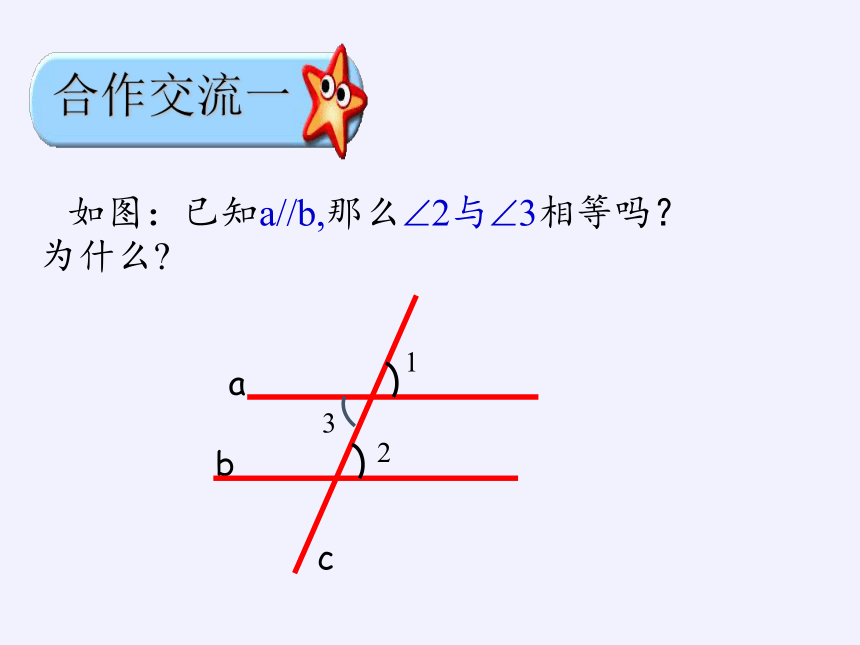
如图:已知a//b,那么 2与 3相等吗?
为什么
合作交流一
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3(两直线平行,内错角相等)
∵a∥b(已知)
几何语言:
简单地说:
b
1
2
a
c
3
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流二
b
1
2
a
c
4
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°(两直线平行,同旁内角互补)
∵a∥b(已知)
几何语言:
简单地说:
b
1
2
a
c
4
结论
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
注意:
只有在两直线平行的条件下才有:同位角、内错角相等,同旁内角互补。并不是所有的同位角、内错角都相等,同旁内角都互补
练习:看图填空
A
B
C
D
E
F
(1)由DE∥BC,可以得到∠ADE= ,依据 是 ;
(2)由DE∥BC ,可以得到∠DFB = ,依据是 ;
(3)由DE∥BC ,可以得到 ∠C+ = 180°,
依据是 ;
(4)由DF∥AC,可以得到 ∠AED= ,依据
是 ;
(5)由DF∥AC ,可以得到∠C = ,依据是
∠B
∠EDF
∠CED
∠EDF
∠BFD
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,内错角相等
两直线平行,同位角相等
两直线平行,同旁内角互补
1
它与地面所
成的较大的
角是多少度
95
0
目前,它与地面所成的较小的角
为∠1=85
2
3
小 结
判 定
性 质
由线定角
由线的位置关系(平行), 定角的数量关系(相等或互补)
由角定线
由角的数量关系(相等或互补),定线的位置关系(平行)
平行线的判定
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的性质
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
课堂作业:
第131习题10.3第4题
课外作业:
基础训练同步
谢 谢
10.3 平行线的性质
数学不是看出来的,也不是单纯想出来的,更重要的是做出来的。
世界著名的意大利比萨斜塔,建于公元1173年,为8层圆柱形建筑,全部用白色大理石砌成,塔高54.5米.
创设情境,复习导入
它与地面所
成的较大的
角是多少度
目前,它与地面所成较小的角
为∠1=85
1
2
3
复习回顾 根据右图,填空:
①如果∠1=∠2,
那么__∥__( )
② 如果∠3=∠2
那么__∥__( )
③ 如果∠3+∠4=180°,
那么__∥__( )
同位角相等
内错角相等
同旁内角互补
两直线平行
AB
CD
AB
CD
同位角相等,两直线平行
内错角相等,两直线平行
AB
CD
同旁内角互补,两直线平行
1
2
3
4
反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢
10.3平行线的性质
a
b
c
在练习本上画两条平行线a、b,再画直线c与直线a、b相交(如下图)
指出图中有几对同位角?
3
4
1
5
2
6
8
7
两直线平行,同位角相等.
平行线的性质1
结论
两条平行线被第三条直线所截,
同位角相等.
性质发现
∴∠1=∠2(两直线平 行,同位角相等)
∵a∥b(已知)
简单地说:
几何语言:
b
1
2
a
c
如图:已知a//b,那么 2与 3相等吗?
为什么
合作交流一
b
1
2
a
c
3
两直线平行,内错角相等.
平行线的性质2
结论
两条平行线被第三条直线所截,
内错角相等.
性质发现
∴∠2=∠3(两直线平行,内错角相等)
∵a∥b(已知)
几何语言:
简单地说:
b
1
2
a
c
3
如图,已知a//b,那么 2与 4有什么关系呢?为什么
合作交流二
b
1
2
a
c
4
两直线平行,同旁内角互补.
平行线的性质3
结论
两条平行线被第三条直线所截,
同旁内角互补.
性质发现
∴ 2+ 4=180°(两直线平行,同旁内角互补)
∵a∥b(已知)
几何语言:
简单地说:
b
1
2
a
c
4
结论
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
注意:
只有在两直线平行的条件下才有:同位角、内错角相等,同旁内角互补。并不是所有的同位角、内错角都相等,同旁内角都互补
练习:看图填空
A
B
C
D
E
F
(1)由DE∥BC,可以得到∠ADE= ,依据 是 ;
(2)由DE∥BC ,可以得到∠DFB = ,依据是 ;
(3)由DE∥BC ,可以得到 ∠C+ = 180°,
依据是 ;
(4)由DF∥AC,可以得到 ∠AED= ,依据
是 ;
(5)由DF∥AC ,可以得到∠C = ,依据是
∠B
∠EDF
∠CED
∠EDF
∠BFD
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,内错角相等
两直线平行,同位角相等
两直线平行,同旁内角互补
1
它与地面所
成的较大的
角是多少度
95
0
目前,它与地面所成的较小的角
为∠1=85
2
3
小 结
判 定
性 质
由线定角
由线的位置关系(平行), 定角的数量关系(相等或互补)
由角定线
由角的数量关系(相等或互补),定线的位置关系(平行)
平行线的判定
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角互补,两直线平行.
平行线的性质
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
课堂作业:
第131习题10.3第4题
课外作业:
基础训练同步
谢 谢
