青岛版九年级数学下册 6.4 随机现象的变化趋势 课件(共15张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 6.4 随机现象的变化趋势 课件(共15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 10:30:42 | ||
图片预览




文档简介
(共15张PPT)
情境导入
猜想:你认为青少年的身高与体重有关系吗?
情境导入
情境导入
假设让你去研究青少年的身高与体重之间的关系,你会怎么做呢?
实验探究
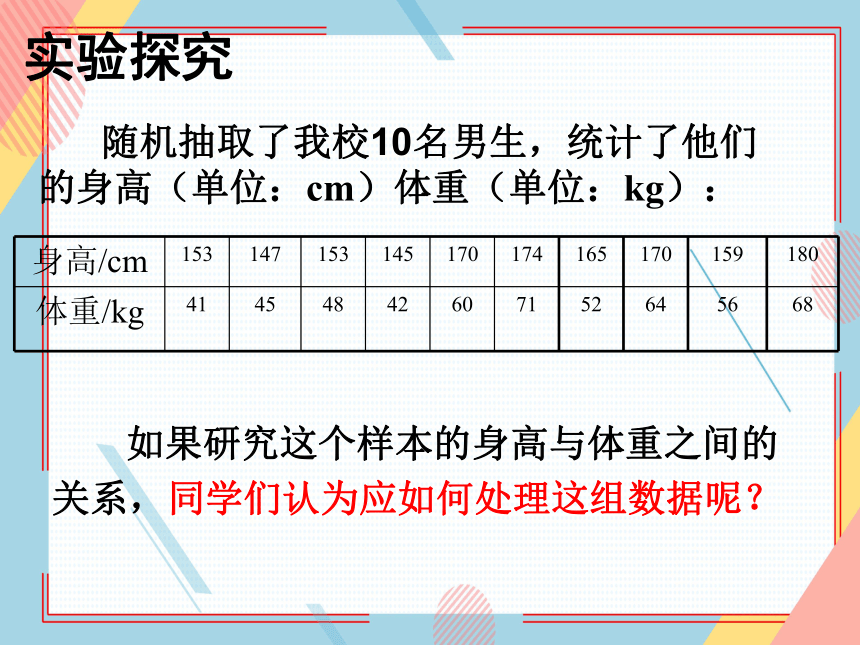
身高/cm 153 147 153 145 170 174 165 170 159 180
体重/kg 41 45 48 42 60 71 52 64 56 68
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
如果研究这个样本的身高与体重之间的关系,同学们认为应如何处理这组数据呢?
实验探究
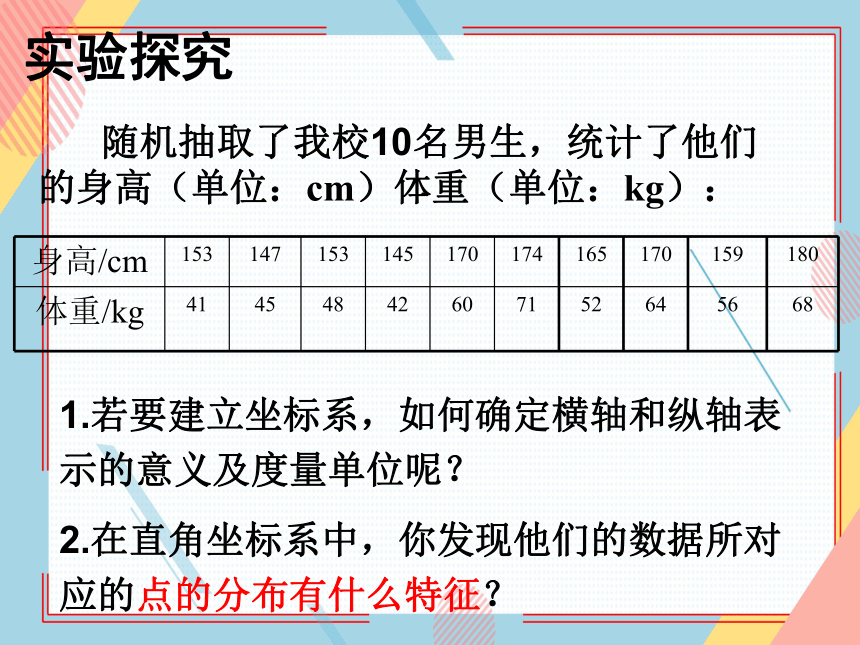
身高/cm 153 147 153 145 170 174 165 170 159 180
体重/kg 41 45 48 42 60 71 52 64 56 68
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
1.若要建立坐标系,如何确定横轴和纵轴表示的意义及度量单位呢?
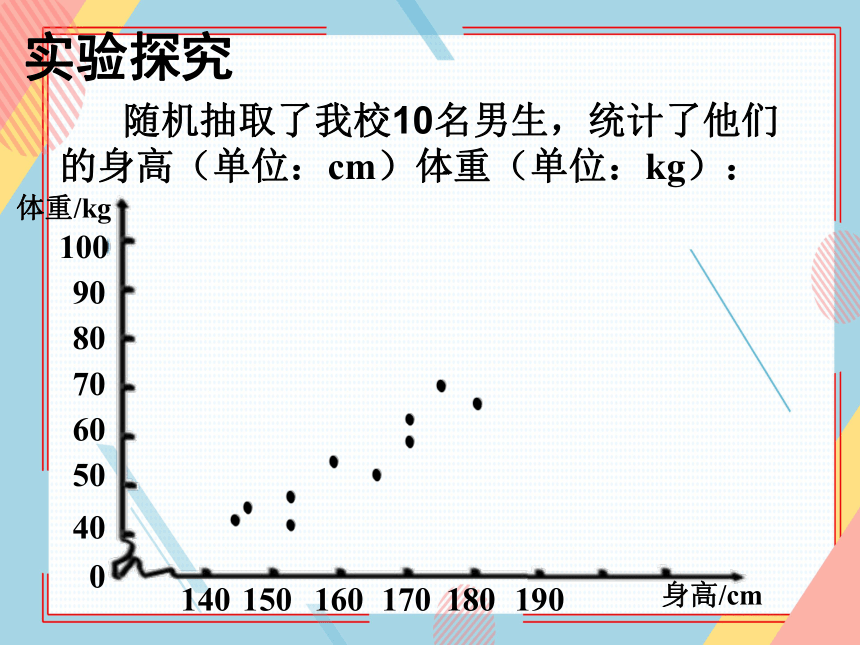
2.在直角坐标系中,你发现他们的数据所对应的点的分布有什么特征?
实验探究
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
40
50
60
70
80
90
100
180
170
160
150
140
0
190
体重/kg
身高/cm
实验探究
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
40
50
60
70
80
90
100
180
170
160
150
140
0
190
体重/kg
身高/cm
实验探究
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
40
50
60
70
80
90
100
180
170
160
150
140
0
190
高中《线性回归方程》给出具体求解的方法
亚洲人G=h-105
身高
体重
阶段总结
变量
依赖关系(不确定)
样本近似估测总体状况
实际问题
相关
函数关系(确定)
建立数学模型
适合
近似
某小卖部为了了解奶茶销售量与气温之间的关系,随机统计并制作了某6天卖出奶茶的杯数与当天气温的对照表:
气温/0C 26 18 13 10 4 -1
杯数 17 24 40 38 50 64
1.通过整理分析数据,你能否找到一条合适的直线表示奶茶杯数与气温的关系?请说明理由?
巩固练习
-5
巩固练习
气温
杯数
2.如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖出奶茶的杯数吗
巩固练习
气温
杯数
-5
y=-3x+56
股票的线性分析(股票的波动有时也在一条带型区域内,找到近似直线描述变化趋势)
课堂延伸
有一些随机现象用一次函数模型无法描述变化趋势(可自行上网查阅).
课堂延伸
情境导入
猜想:你认为青少年的身高与体重有关系吗?
情境导入
情境导入
假设让你去研究青少年的身高与体重之间的关系,你会怎么做呢?
实验探究
身高/cm 153 147 153 145 170 174 165 170 159 180
体重/kg 41 45 48 42 60 71 52 64 56 68
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
如果研究这个样本的身高与体重之间的关系,同学们认为应如何处理这组数据呢?
实验探究
身高/cm 153 147 153 145 170 174 165 170 159 180
体重/kg 41 45 48 42 60 71 52 64 56 68
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
1.若要建立坐标系,如何确定横轴和纵轴表示的意义及度量单位呢?
2.在直角坐标系中,你发现他们的数据所对应的点的分布有什么特征?
实验探究
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
40
50
60
70
80
90
100
180
170
160
150
140
0
190
体重/kg
身高/cm
实验探究
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
40
50
60
70
80
90
100
180
170
160
150
140
0
190
体重/kg
身高/cm
实验探究
随机抽取了我校10名男生,统计了他们的身高(单位:cm)体重(单位:kg):
40
50
60
70
80
90
100
180
170
160
150
140
0
190
高中《线性回归方程》给出具体求解的方法
亚洲人G=h-105
身高
体重
阶段总结
变量
依赖关系(不确定)
样本近似估测总体状况
实际问题
相关
函数关系(确定)
建立数学模型
适合
近似
某小卖部为了了解奶茶销售量与气温之间的关系,随机统计并制作了某6天卖出奶茶的杯数与当天气温的对照表:
气温/0C 26 18 13 10 4 -1
杯数 17 24 40 38 50 64
1.通过整理分析数据,你能否找到一条合适的直线表示奶茶杯数与气温的关系?请说明理由?
巩固练习
-5
巩固练习
气温
杯数
2.如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖出奶茶的杯数吗
巩固练习
气温
杯数
-5
y=-3x+56
股票的线性分析(股票的波动有时也在一条带型区域内,找到近似直线描述变化趋势)
课堂延伸
有一些随机现象用一次函数模型无法描述变化趋势(可自行上网查阅).
课堂延伸
