数学北师大版(2019)必修第二册 6.3..2刻画空间点、线、面位置关系的公理二 课件(共34张PPT)
文档属性
| 名称 | 数学北师大版(2019)必修第二册 6.3..2刻画空间点、线、面位置关系的公理二 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 18:07:23 | ||
图片预览









文档简介
(共34张PPT)
6.3.2 刻画空间点、线、面位置关系的公理(二)
课标阐释
1.掌握基本事实4及等角定理的含义及作用,能解决有关平行或角度的证明问题.(数学抽象、逻辑推理)
2.掌握异面直线所成角的概念,能求出一些较特殊的异面直线所成的角.(数学运算、几何直观)
3.理解空间四边形的结构特点,并能找出与平面四边形的异同.(几何直观)
思维脉络
激趣诱思
知识点拨
立体交叉桥,简称立交桥.随着世界各国经济的发展和高速公路的出现,现代化的城市道路交通开始朝立体化发展.世界上第一座立交桥是于1928年由美国建造的,此后世界各地的
立交桥相继出现.1952年,我国于北京滨河路兴建了首座立交桥.全国第二座立交桥是于1962年在广州修建的.现在的立交桥已由最初的上、下两层分开式,向多层次、多方向的复杂立体交叉方式发展,目的是大力提高交叉路口的车流速度,并确保交通安全.若把立交桥抽象成直线,它们在同一个平面内吗 这样的直线有何特征 一条南北走向和一条东西走向(不同层)的立交桥所在直线的夹角如何刻画
激趣诱思
知识点拨
一、基本事实4
1.文字表述:平行于同一条直线的两条直线互相平行.这一性质通常称为空间平行线的传递性.
名师点析基本事实4说明把平行线的传递性推广到空间也能成立,这个基本性质是判断两条直线平行的重要方法之一,其关键在于寻找联系所证两条平行直线的第三条直线.
激趣诱思
知识点拨
微练习
已知直线a∥直线b,直线b∥直线c,直线c∥直线d,则a与d的位置关系是( )
A.平行 B.相交
C.异面 D.不确定
解析因为a∥b,b∥c,所以a∥c.又c∥d,所以a∥d.
答案A
激趣诱思
知识点拨
二、空间两直线的位置关系
1.异面直线
定义:不同在任何一个平面内(不共面)的两条直线.
2.空间两条直线的位置关系有且只有三种:
激趣诱思
知识点拨
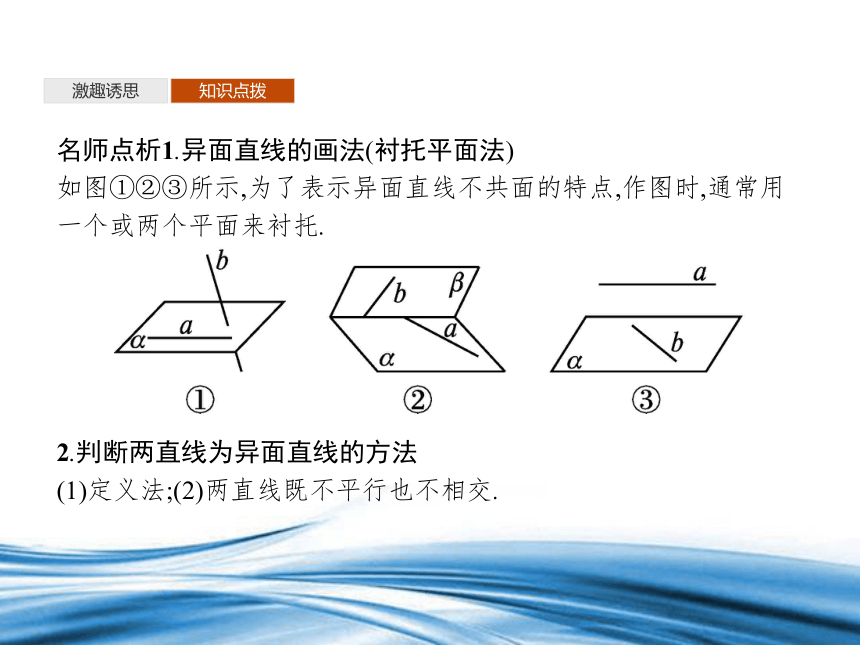
名师点析1.异面直线的画法(衬托平面法)
如图①②③所示,为了表示异面直线不共面的特点,作图时,通常用一个或两个平面来衬托.
2.判断两直线为异面直线的方法
(1)定义法;(2)两直线既不平行也不相交.
激趣诱思
知识点拨
微思考
分别在两个平面内的两条直线一定是异面直线吗
提示不一定,它们可能相交,可能平行,也可能异面.
微判断
判断(正确的打“√”,错误的打“×”).
(1)没有公共点的两条直线是异面直线.( )
(2)两直线若不是异面直线,则必相交或平行.( )
(3)如果直线a与直线b是异面直线,直线b与直线c也是异面直线,那么直线a与直线c也一定是异面直线.( )
(4)四个顶点不在同一平面内,且边长相等的四边形是不存在的.( )
答案(1)× (2)√ (3)× (4)×
激趣诱思
知识点拨
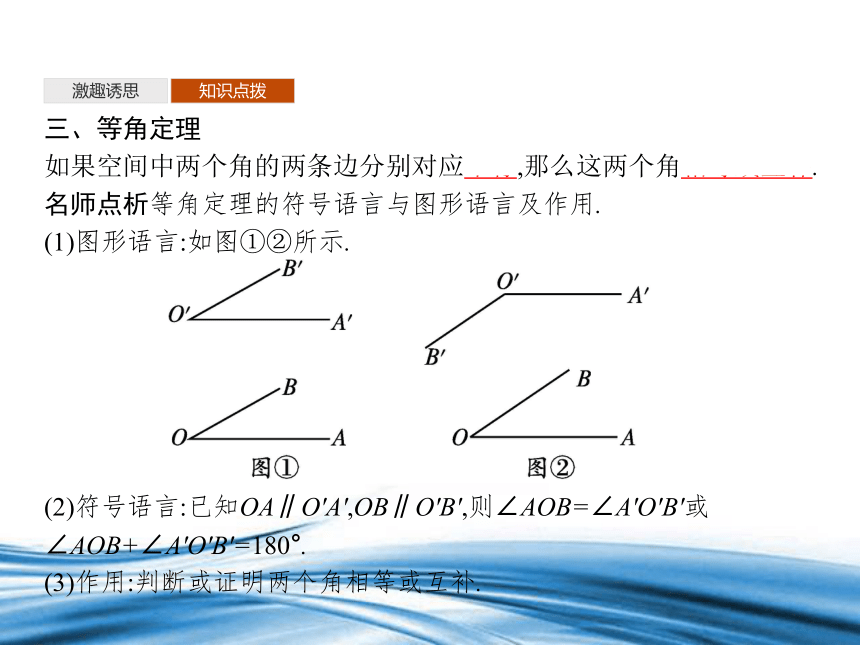
三、等角定理
如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
名师点析等角定理的符号语言与图形语言及作用.
(1)图形语言:如图①②所示.
(2)符号语言:已知OA∥O'A',OB∥O'B',则∠AOB=∠A'O'B'或∠AOB+∠A'O'B'=180°.
(3)作用:判断或证明两个角相等或互补.
激趣诱思
知识点拨
微练习
空间两个角α,β的两边分别对应平行,且方向相同,若α=50°,则β等于( )
A.50° B.130°
C.40° D.50°或130°
解析因为α,β的两边分别对应平行,且方向相同,由等角定理知β与α相等.
答案A
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)两条直线和第三条直线成等角,则这两条直线平行.( )
(2)如果两个角的对应边互相平行,且方向都相反,则两个角互补.( )
答案(1)× (2)×
激趣诱思
知识点拨
四、异面直线所成的角
定义 前提 两条异面直线a,b
作法 过空间任一点O作直线a'∥a,b'∥b,这时a',b'共面
结论 我们把a'与b'所成的不大于90°的角称为异面直线a,b所成的角(或夹角)
特殊 情况 若两条异面直线a,b所成的角是直角,则称这两条直线互相垂直,记作:a⊥b
名师点析1.若两条异面直线a,b所成的角为θ,则θ的范围为0°<θ≤90°;
2.求解两条异面直线所成的角的过程体现了把空间图形问题平面化的化归数学思想.
激趣诱思
知识点拨
微练习
如图所示,在四面体ABCD中,E,F,G分别为BC,AD,DB的中点,若AB与CD所成的角为60°,则∠FGE= .
解析因为E,F,G分别为BC,AD,DB的中点,所以FG∥AB,EG∥DC,所以∠FGE=60°或120°.
答案60°或120°
探究一
探究二
探究三
探究四
当堂检测
基本事实4的应用
探究一
探究二
探究三
探究四
当堂检测
证明如图所示,连接PD,PE,并延长分别交AB,BC于点M,N.
因为点D,E分别是△PAB,△PBC的重心,所以M,N分别是AB,BC的中点.
探究一
探究二
探究三
探究四
当堂检测
变式训练1如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱A1A,C1C的中点,求证:四边形MBND1为平行四边形.
探究一
探究二
探究三
探究四
当堂检测
证明取B1B的中点P,连接C1P,MP.
因为N为C1C的中点,
由正方体的性质知C1N PB,
所以四边形C1PBN为平行四边形,所以C1P BN.
又M,P分别为A1A,B1B的中点,所以MP A1B1.
又由正方体的性质知A1B1 C1D1,所以MP C1D1,
所以四边形D1MPC1为平行四边形,
所以C1P MD1.所以MD1 BN,
所以四边形MBND1为平行四边形.
探究一
探究二
探究三
探究四
当堂检测
异面直线的判定
例2如图是一个正方体的展开图,如果将它还原为正方体,那么NC,DE,AF,BM这四条线段所在的直线是异面直线的有多少对 试以其中一对为例进行证明.
探究一
探究二
探究三
探究四
当堂检测
解将展开图还原为正方体(如图).
直线NC与直线DE,直线NC与直线AF,直线NC与直线BM,直线DE与直线AF,直线DE与直线BM,直线AF与直线BM,都是异面直线,共有6对.
以直线NC与直线AF是异面直线为例证明如下:
(方法一)连接BE,若NC∥AF,
则由NC∥BE,可知AF∥BE,
这与直线AF与直线BE相交矛盾.
故直线NC与直线AF不平行.
若直线NC与直线AF相交,则平面ABFE与平面CDNM有公共点,这与正方体的性质矛盾.故直线NC与直线AF不相交.
所以直线NC与直线AF异面.
探究一
探究二
探究三
探究四
当堂检测
(方法二)连接BE,如图,因为直线NC 平面BCNE,
直线AF∩平面BCNE=O.
O 直线NC,所以直线NC与直线AF异面.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 判定两条直线是异面直线的方法
(1)证明两条直线既不平行又不相交.
(2)重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图).
探究一
探究二
探究三
探究四
当堂检测
变式训练2分别在两个相交平面内的两条直线间的位置关系是( )
A.异面 B.平行 C.相交 D.以上都有可能
解析如图①所示,直线a与b互相平行;如图②所示,直线a与b相交;如图③所示,直线a与b异面.
答案D
探究一
探究二
探究三
探究四
当堂检测
等角定理的应用
例3如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.求证:
(1)四边形BB1M1M为平行四边形;
(2)∠BMC=∠B1M1C1.
探究一
探究二
探究三
探究四
当堂检测
证明(1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,所以A1M1∥AM,且A1M1=AM,
所以四边形AMM1A1是平行四边形,
所以A1A∥M1M,且A1A=M1M.
又因为A1A∥B1B,且A1A=B1B,
所以M1M∥B1B,且M1M=B1B,
所以四边形BB1M1M为平行四边形.
(2)由(1)知四边形BB1M1M为平行四边形,
所以B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
所以C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.
所以∠BMC=∠B1M1C1.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 有关证明角相等问题,一般采用下面三种途径
(1)利用等角定理.
(2)利用三角形相似.
(3)利用三角形全等.
本例是通过第一种途径来实现的.
探究一
探究二
探究三
探究四
当堂检测
延伸探究将本例中的条件“M,M1分别是棱AD和A1D1的中点”改为“M,N分别是棱CD,AD的中点”,其他条件不变,求证:
(1)四边形MNA1C1是梯形;
(2)∠DNM=∠D1A1C1.
探究一
探究二
探究三
探究四
当堂检测
探究一
探究二
探究三
探究四
当堂检测
探究一
探究二
探究三
探究四
当堂检测
反思感悟 因空间图形往往包含平面图形,故在解答与空间四边形有关的问题时,常借助平面几何中的有关性质或定理.
探究一
探究二
探究三
探究四
当堂检测
变式训练3已知空间四面体ABCD中,AB≠AC,BD=BC,AE是△ABC的边BC上的高,DF是△BCD的边BC上的中线,判定AE与DF的位置关系.
解由已知,得E,F不重合.设△BCD所在平面为α,则DF α,A α,E∈α,E DF,所以AE与DF异面.
探究一
探究二
探究三
探究四
当堂检测
1.(多选)如图所示,在长方体ABCD-A1B1C1D1中,与AA1不是异面直线的有( )
A.AB B.BB1 C.DD1 D.B1C1
解析由异面直线的定义知,与AA1异面的直线应为B1C1,其他选项与AA1均为平行或相交的位置关系.
答案ABC
探究一
探究二
探究三
探究四
当堂检测
2.若∠AOB=∠A'O'B',OA∥O'A',且OA与O'A'的方向相同,则OB与O'B'( )
A.一定平行,且方向相同 B.一定平行,且方向相反
C.一定不平行 D.不一定平行
解析由于两角不一定在同一个平面内或两角所在的平面不一定平行,因此OB与O'B'不一定平行.
答案D
探究一
探究二
探究三
探究四
当堂检测
3.如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明连接BD.
由题意知EH是△ABD的中位线,
因此EH FG.
故四边形EFGH为平行四边形.
6.3.2 刻画空间点、线、面位置关系的公理(二)
课标阐释
1.掌握基本事实4及等角定理的含义及作用,能解决有关平行或角度的证明问题.(数学抽象、逻辑推理)
2.掌握异面直线所成角的概念,能求出一些较特殊的异面直线所成的角.(数学运算、几何直观)
3.理解空间四边形的结构特点,并能找出与平面四边形的异同.(几何直观)
思维脉络
激趣诱思
知识点拨
立体交叉桥,简称立交桥.随着世界各国经济的发展和高速公路的出现,现代化的城市道路交通开始朝立体化发展.世界上第一座立交桥是于1928年由美国建造的,此后世界各地的
立交桥相继出现.1952年,我国于北京滨河路兴建了首座立交桥.全国第二座立交桥是于1962年在广州修建的.现在的立交桥已由最初的上、下两层分开式,向多层次、多方向的复杂立体交叉方式发展,目的是大力提高交叉路口的车流速度,并确保交通安全.若把立交桥抽象成直线,它们在同一个平面内吗 这样的直线有何特征 一条南北走向和一条东西走向(不同层)的立交桥所在直线的夹角如何刻画
激趣诱思
知识点拨
一、基本事实4
1.文字表述:平行于同一条直线的两条直线互相平行.这一性质通常称为空间平行线的传递性.
名师点析基本事实4说明把平行线的传递性推广到空间也能成立,这个基本性质是判断两条直线平行的重要方法之一,其关键在于寻找联系所证两条平行直线的第三条直线.
激趣诱思
知识点拨
微练习
已知直线a∥直线b,直线b∥直线c,直线c∥直线d,则a与d的位置关系是( )
A.平行 B.相交
C.异面 D.不确定
解析因为a∥b,b∥c,所以a∥c.又c∥d,所以a∥d.
答案A
激趣诱思
知识点拨
二、空间两直线的位置关系
1.异面直线
定义:不同在任何一个平面内(不共面)的两条直线.
2.空间两条直线的位置关系有且只有三种:
激趣诱思
知识点拨
名师点析1.异面直线的画法(衬托平面法)
如图①②③所示,为了表示异面直线不共面的特点,作图时,通常用一个或两个平面来衬托.
2.判断两直线为异面直线的方法
(1)定义法;(2)两直线既不平行也不相交.
激趣诱思
知识点拨
微思考
分别在两个平面内的两条直线一定是异面直线吗
提示不一定,它们可能相交,可能平行,也可能异面.
微判断
判断(正确的打“√”,错误的打“×”).
(1)没有公共点的两条直线是异面直线.( )
(2)两直线若不是异面直线,则必相交或平行.( )
(3)如果直线a与直线b是异面直线,直线b与直线c也是异面直线,那么直线a与直线c也一定是异面直线.( )
(4)四个顶点不在同一平面内,且边长相等的四边形是不存在的.( )
答案(1)× (2)√ (3)× (4)×
激趣诱思
知识点拨
三、等角定理
如果空间中两个角的两条边分别对应平行,那么这两个角相等或互补.
名师点析等角定理的符号语言与图形语言及作用.
(1)图形语言:如图①②所示.
(2)符号语言:已知OA∥O'A',OB∥O'B',则∠AOB=∠A'O'B'或∠AOB+∠A'O'B'=180°.
(3)作用:判断或证明两个角相等或互补.
激趣诱思
知识点拨
微练习
空间两个角α,β的两边分别对应平行,且方向相同,若α=50°,则β等于( )
A.50° B.130°
C.40° D.50°或130°
解析因为α,β的两边分别对应平行,且方向相同,由等角定理知β与α相等.
答案A
激趣诱思
知识点拨
微判断
判断(正确的打“√”,错误的打“×”).
(1)两条直线和第三条直线成等角,则这两条直线平行.( )
(2)如果两个角的对应边互相平行,且方向都相反,则两个角互补.( )
答案(1)× (2)×
激趣诱思
知识点拨
四、异面直线所成的角
定义 前提 两条异面直线a,b
作法 过空间任一点O作直线a'∥a,b'∥b,这时a',b'共面
结论 我们把a'与b'所成的不大于90°的角称为异面直线a,b所成的角(或夹角)
特殊 情况 若两条异面直线a,b所成的角是直角,则称这两条直线互相垂直,记作:a⊥b
名师点析1.若两条异面直线a,b所成的角为θ,则θ的范围为0°<θ≤90°;
2.求解两条异面直线所成的角的过程体现了把空间图形问题平面化的化归数学思想.
激趣诱思
知识点拨
微练习
如图所示,在四面体ABCD中,E,F,G分别为BC,AD,DB的中点,若AB与CD所成的角为60°,则∠FGE= .
解析因为E,F,G分别为BC,AD,DB的中点,所以FG∥AB,EG∥DC,所以∠FGE=60°或120°.
答案60°或120°
探究一
探究二
探究三
探究四
当堂检测
基本事实4的应用
探究一
探究二
探究三
探究四
当堂检测
证明如图所示,连接PD,PE,并延长分别交AB,BC于点M,N.
因为点D,E分别是△PAB,△PBC的重心,所以M,N分别是AB,BC的中点.
探究一
探究二
探究三
探究四
当堂检测
变式训练1如图所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱A1A,C1C的中点,求证:四边形MBND1为平行四边形.
探究一
探究二
探究三
探究四
当堂检测
证明取B1B的中点P,连接C1P,MP.
因为N为C1C的中点,
由正方体的性质知C1N PB,
所以四边形C1PBN为平行四边形,所以C1P BN.
又M,P分别为A1A,B1B的中点,所以MP A1B1.
又由正方体的性质知A1B1 C1D1,所以MP C1D1,
所以四边形D1MPC1为平行四边形,
所以C1P MD1.所以MD1 BN,
所以四边形MBND1为平行四边形.
探究一
探究二
探究三
探究四
当堂检测
异面直线的判定
例2如图是一个正方体的展开图,如果将它还原为正方体,那么NC,DE,AF,BM这四条线段所在的直线是异面直线的有多少对 试以其中一对为例进行证明.
探究一
探究二
探究三
探究四
当堂检测
解将展开图还原为正方体(如图).
直线NC与直线DE,直线NC与直线AF,直线NC与直线BM,直线DE与直线AF,直线DE与直线BM,直线AF与直线BM,都是异面直线,共有6对.
以直线NC与直线AF是异面直线为例证明如下:
(方法一)连接BE,若NC∥AF,
则由NC∥BE,可知AF∥BE,
这与直线AF与直线BE相交矛盾.
故直线NC与直线AF不平行.
若直线NC与直线AF相交,则平面ABFE与平面CDNM有公共点,这与正方体的性质矛盾.故直线NC与直线AF不相交.
所以直线NC与直线AF异面.
探究一
探究二
探究三
探究四
当堂检测
(方法二)连接BE,如图,因为直线NC 平面BCNE,
直线AF∩平面BCNE=O.
O 直线NC,所以直线NC与直线AF异面.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 判定两条直线是异面直线的方法
(1)证明两条直线既不平行又不相交.
(2)重要结论:连接平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.用符号语言可表示为A α,B∈α,l α,B l AB与l是异面直线(如图).
探究一
探究二
探究三
探究四
当堂检测
变式训练2分别在两个相交平面内的两条直线间的位置关系是( )
A.异面 B.平行 C.相交 D.以上都有可能
解析如图①所示,直线a与b互相平行;如图②所示,直线a与b相交;如图③所示,直线a与b异面.
答案D
探究一
探究二
探究三
探究四
当堂检测
等角定理的应用
例3如图,在正方体ABCD-A1B1C1D1中,M,M1分别是棱AD和A1D1的中点.求证:
(1)四边形BB1M1M为平行四边形;
(2)∠BMC=∠B1M1C1.
探究一
探究二
探究三
探究四
当堂检测
证明(1)在正方形ADD1A1中,M,M1分别为AD,A1D1的中点,所以A1M1∥AM,且A1M1=AM,
所以四边形AMM1A1是平行四边形,
所以A1A∥M1M,且A1A=M1M.
又因为A1A∥B1B,且A1A=B1B,
所以M1M∥B1B,且M1M=B1B,
所以四边形BB1M1M为平行四边形.
(2)由(1)知四边形BB1M1M为平行四边形,
所以B1M1∥BM.
同理可得四边形CC1M1M为平行四边形,
所以C1M1∥CM.
由平面几何知识可知,∠BMC和∠B1M1C1都是锐角.
所以∠BMC=∠B1M1C1.
探究一
探究二
探究三
探究四
当堂检测
反思感悟 有关证明角相等问题,一般采用下面三种途径
(1)利用等角定理.
(2)利用三角形相似.
(3)利用三角形全等.
本例是通过第一种途径来实现的.
探究一
探究二
探究三
探究四
当堂检测
延伸探究将本例中的条件“M,M1分别是棱AD和A1D1的中点”改为“M,N分别是棱CD,AD的中点”,其他条件不变,求证:
(1)四边形MNA1C1是梯形;
(2)∠DNM=∠D1A1C1.
探究一
探究二
探究三
探究四
当堂检测
探究一
探究二
探究三
探究四
当堂检测
探究一
探究二
探究三
探究四
当堂检测
反思感悟 因空间图形往往包含平面图形,故在解答与空间四边形有关的问题时,常借助平面几何中的有关性质或定理.
探究一
探究二
探究三
探究四
当堂检测
变式训练3已知空间四面体ABCD中,AB≠AC,BD=BC,AE是△ABC的边BC上的高,DF是△BCD的边BC上的中线,判定AE与DF的位置关系.
解由已知,得E,F不重合.设△BCD所在平面为α,则DF α,A α,E∈α,E DF,所以AE与DF异面.
探究一
探究二
探究三
探究四
当堂检测
1.(多选)如图所示,在长方体ABCD-A1B1C1D1中,与AA1不是异面直线的有( )
A.AB B.BB1 C.DD1 D.B1C1
解析由异面直线的定义知,与AA1异面的直线应为B1C1,其他选项与AA1均为平行或相交的位置关系.
答案ABC
探究一
探究二
探究三
探究四
当堂检测
2.若∠AOB=∠A'O'B',OA∥O'A',且OA与O'A'的方向相同,则OB与O'B'( )
A.一定平行,且方向相同 B.一定平行,且方向相反
C.一定不平行 D.不一定平行
解析由于两角不一定在同一个平面内或两角所在的平面不一定平行,因此OB与O'B'不一定平行.
答案D
探究一
探究二
探究三
探究四
当堂检测
3.如图,在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证:四边形EFGH是平行四边形.
证明连接BD.
由题意知EH是△ABD的中位线,
因此EH FG.
故四边形EFGH为平行四边形.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
