鲁科版(五四制)物理八年级下 第八章 第二节 阿基米德原理 课件(共22张PPT)
文档属性
| 名称 | 鲁科版(五四制)物理八年级下 第八章 第二节 阿基米德原理 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(五四制) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-20 06:22:12 | ||
图片预览






文档简介
(共22张PPT)
第二节 阿基米德原理
他的名言:给我一个支点,我将撬动整个地球
阿基米德(Archimedes,前287~前212)是古希腊伟大的科学家。他在物理学方面的贡献主要有两项:
一是关于浮力问题;
二是关于杠杆平衡问题。
1.求物体上下表面的压力差
F浮=F向上-F向下
复习
2.一切浸入液体中的物体都受到浮力的作用
F浮=G-F拉(称重法)
。。。。。。。。。
求浮力大小
回顾结论:浮力大小与哪些因素有关?
浮力大小,跟它浸在液体中的体积和液体的密度有关。
浸在液体中的体积越大、液体的密度越大,浮力就越大。
现象:
(1)把鸡蛋放入清水中,然后加盐,改变液体的密度;
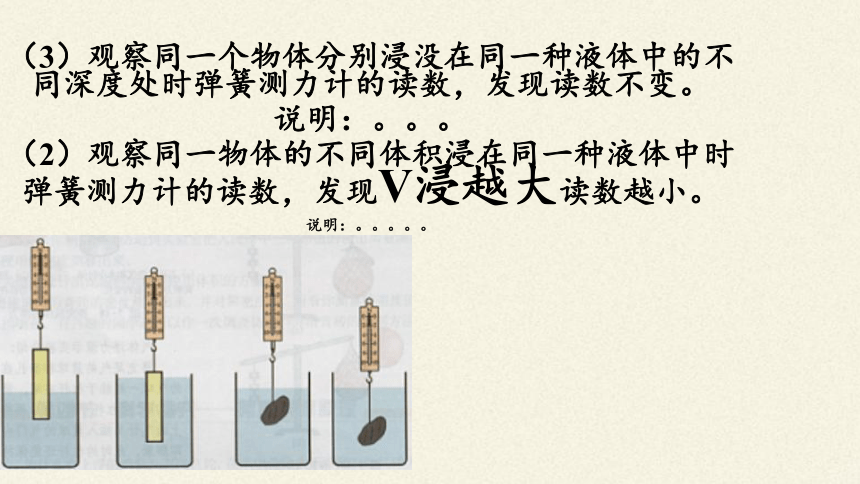
(3)观察同一个物体分别浸没在同一种液体中的不同深度处时弹簧测力计的读数,发现读数不变。
说明:。。。
(2)观察同一物体的不同体积浸在同一种液体中时弹簧测力计的读数,发现V浸越大读数越小。
说明:。。。。。
阿基米德又有新发现
一天,他跨进盛满水的浴缸洗澡时,看见浴缸里的水向外溢,他忽然想到:物体浸在液体中的体积,不就是物体排开液体的体积吗?
读了这一故事,对你有什么启示
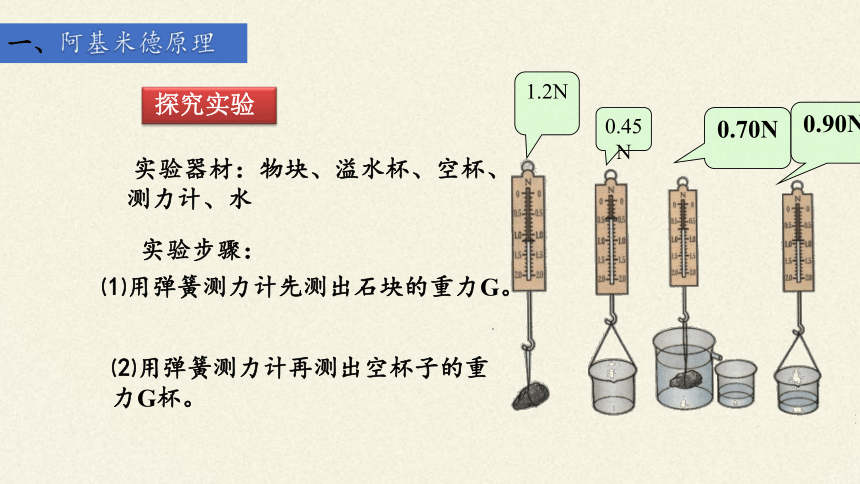
实验器材:物块、溢水杯、空杯、测力计、水
⑴用弹簧测力计先测出石块的重力G。
⑵用弹簧测力计再测出空杯子的重力G杯。
1.2N
0.45N
实验步骤:
一、阿基米德原理
探究实验
0.70N
0.90N
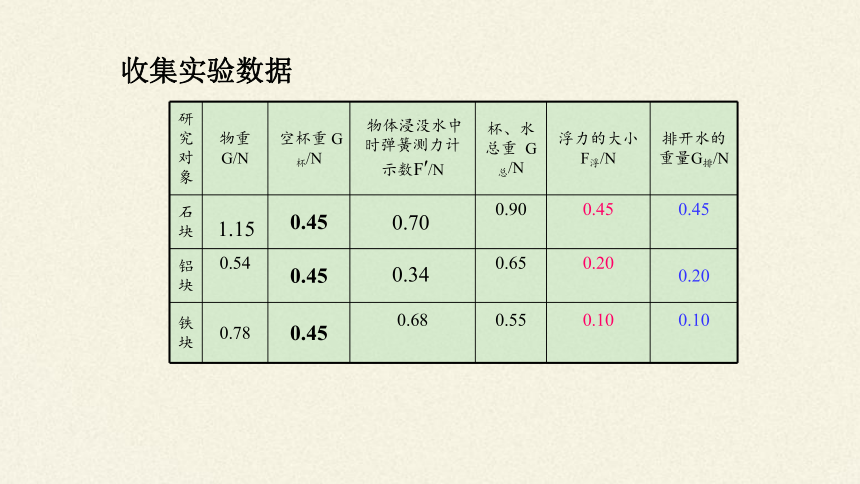
研究对象 物重G/N 空杯重 G杯/N 物体浸没水中时弹簧测力计 示数F′/N 杯、水总重 G总/N 浮力的大小 F浮/N 排开水的重量G排/N
石块 0.45 0.90 0.45 0.45
铝块 0.54 0.45 0.65 0.20 0.20
铁块 0.78 0.45 0.68 0.55 0.10 0.10
1.15
0.70
0.34
收集实验数据
阿基米德原理
1.内容:
浸在液体里的物体受到向上的浮力,浮力的大小等于物体排开的液体受到的重力。
2.公式:
F浮=G排=ρ液 g V排
1.一个物体所受的重力为10N,将其全部浸没在水中时,排开重20N的水,此时它所受的浮力为_ N。
20
分析:已知G排=20N,所以F浮=G排=20N。
2.将金属块的一半浸没水中,排开了0.6kg的水,金属块受到的浮力是 N。
6
分析:已知m排=0.6kg,
所以F浮=m排 g=0.6kg×10N/kg=6N。
3.对原理的理解
(1)物体“浸在液体里”包括“全部浸入(即浸没)”和“部分浸入”两种情况。区分:浸没、浸入、浸在、没入;
不论物体是浸没还是部分浸入在液体里都受到浮力。对于同一物体而言,浸没时受到的浮力大,部分浸入时受到的浮力小,而且浸入的体积越小,所受的浮力也越小。
浸没
部分浸入
(2)阿基米德原理同样适用于气体。
G
托力
气体的浮力
气体与液体一样对浸在其中的物体,也具有竖直向上的力,即也有浮力的作用。
实验证明,阿基米德原理对气体同样适用。
典例:(已知地面附近气温是0℃,气压是1×105Pa,空气的密度是1.3kg/m3 ,g=10N/kg)一个在节日放飞的气球,体积是600m3,这个气球在地面附近受到的浮力有多大?
解:根据阿基米德原理:
F浮=ρ空气gV排 =1.3kg/m3×10N/kg×600m3=7800N
答:这个气球在地面附近受到的浮力为7800N
3.F浮= ρ液 gV排 —— 决定式
表明浮力大小只和 ρ液 、V排有关,
浮力大小与物体的形状、密度,浸没在液体中的深度及物体在液体中是否运动等因素无关。
2、一个2N的物体,挂在弹簧测力计上,当钩码浸没在水中时弹簧测力计的示数是1.2N,这个钩码受到水的浮力是 N
0.8
3、 某物体重0.5N,把它放入盛有水的烧杯中,溢出重为0.3N的水,则它受到的浮力为( )
A.一定为0.3N. B.可能为0.2N.
C.一定为0.5N. D.可能为0.4N.
D
4、比较下列物体受的浮力
⑴体积相同的铜、铁、铝浸没水中
铁
F浮铝 = F浮铁= F浮铜
铜
铝
⑵如图所示,A、B两个物体的体积相
等,哪个受到的浮力大?
A
B
F浮A< F浮B
4、比较下列物体受的浮力
拓展:质量都是是1kg的实心铜球和铝球,浸没水中, 受到的浮力大.
铜
铝
(ρ铜>ρ铝)
4、比较下列物体受的浮力
铝球
1.阿基米德原理的探究实验
2.阿基米德原理的数学表达式
3.阿基米德原理的公式理解(难点)
4.利用阿基米德原理的分析与计算(重点)
知识梳理
谢 谢
第二节 阿基米德原理
他的名言:给我一个支点,我将撬动整个地球
阿基米德(Archimedes,前287~前212)是古希腊伟大的科学家。他在物理学方面的贡献主要有两项:
一是关于浮力问题;
二是关于杠杆平衡问题。
1.求物体上下表面的压力差
F浮=F向上-F向下
复习
2.一切浸入液体中的物体都受到浮力的作用
F浮=G-F拉(称重法)
。。。。。。。。。
求浮力大小
回顾结论:浮力大小与哪些因素有关?
浮力大小,跟它浸在液体中的体积和液体的密度有关。
浸在液体中的体积越大、液体的密度越大,浮力就越大。
现象:
(1)把鸡蛋放入清水中,然后加盐,改变液体的密度;
(3)观察同一个物体分别浸没在同一种液体中的不同深度处时弹簧测力计的读数,发现读数不变。
说明:。。。
(2)观察同一物体的不同体积浸在同一种液体中时弹簧测力计的读数,发现V浸越大读数越小。
说明:。。。。。
阿基米德又有新发现
一天,他跨进盛满水的浴缸洗澡时,看见浴缸里的水向外溢,他忽然想到:物体浸在液体中的体积,不就是物体排开液体的体积吗?
读了这一故事,对你有什么启示
实验器材:物块、溢水杯、空杯、测力计、水
⑴用弹簧测力计先测出石块的重力G。
⑵用弹簧测力计再测出空杯子的重力G杯。
1.2N
0.45N
实验步骤:
一、阿基米德原理
探究实验
0.70N
0.90N
研究对象 物重G/N 空杯重 G杯/N 物体浸没水中时弹簧测力计 示数F′/N 杯、水总重 G总/N 浮力的大小 F浮/N 排开水的重量G排/N
石块 0.45 0.90 0.45 0.45
铝块 0.54 0.45 0.65 0.20 0.20
铁块 0.78 0.45 0.68 0.55 0.10 0.10
1.15
0.70
0.34
收集实验数据
阿基米德原理
1.内容:
浸在液体里的物体受到向上的浮力,浮力的大小等于物体排开的液体受到的重力。
2.公式:
F浮=G排=ρ液 g V排
1.一个物体所受的重力为10N,将其全部浸没在水中时,排开重20N的水,此时它所受的浮力为_ N。
20
分析:已知G排=20N,所以F浮=G排=20N。
2.将金属块的一半浸没水中,排开了0.6kg的水,金属块受到的浮力是 N。
6
分析:已知m排=0.6kg,
所以F浮=m排 g=0.6kg×10N/kg=6N。
3.对原理的理解
(1)物体“浸在液体里”包括“全部浸入(即浸没)”和“部分浸入”两种情况。区分:浸没、浸入、浸在、没入;
不论物体是浸没还是部分浸入在液体里都受到浮力。对于同一物体而言,浸没时受到的浮力大,部分浸入时受到的浮力小,而且浸入的体积越小,所受的浮力也越小。
浸没
部分浸入
(2)阿基米德原理同样适用于气体。
G
托力
气体的浮力
气体与液体一样对浸在其中的物体,也具有竖直向上的力,即也有浮力的作用。
实验证明,阿基米德原理对气体同样适用。
典例:(已知地面附近气温是0℃,气压是1×105Pa,空气的密度是1.3kg/m3 ,g=10N/kg)一个在节日放飞的气球,体积是600m3,这个气球在地面附近受到的浮力有多大?
解:根据阿基米德原理:
F浮=ρ空气gV排 =1.3kg/m3×10N/kg×600m3=7800N
答:这个气球在地面附近受到的浮力为7800N
3.F浮= ρ液 gV排 —— 决定式
表明浮力大小只和 ρ液 、V排有关,
浮力大小与物体的形状、密度,浸没在液体中的深度及物体在液体中是否运动等因素无关。
2、一个2N的物体,挂在弹簧测力计上,当钩码浸没在水中时弹簧测力计的示数是1.2N,这个钩码受到水的浮力是 N
0.8
3、 某物体重0.5N,把它放入盛有水的烧杯中,溢出重为0.3N的水,则它受到的浮力为( )
A.一定为0.3N. B.可能为0.2N.
C.一定为0.5N. D.可能为0.4N.
D
4、比较下列物体受的浮力
⑴体积相同的铜、铁、铝浸没水中
铁
F浮铝 = F浮铁= F浮铜
铜
铝
⑵如图所示,A、B两个物体的体积相
等,哪个受到的浮力大?
A
B
F浮A< F浮B
4、比较下列物体受的浮力
拓展:质量都是是1kg的实心铜球和铝球,浸没水中, 受到的浮力大.
铜
铝
(ρ铜>ρ铝)
4、比较下列物体受的浮力
铝球
1.阿基米德原理的探究实验
2.阿基米德原理的数学表达式
3.阿基米德原理的公式理解(难点)
4.利用阿基米德原理的分析与计算(重点)
知识梳理
谢 谢
