2021-2022学年鲁教版(五四学制)六年级数学下册期中复习综合练习题(word版 含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四学制)六年级数学下册期中复习综合练习题(word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 71.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-20 15:24:07 | ||
图片预览



文档简介
2021-2022学年鲁教版(五四学制)六年级数学下册期中复习综合练习题(附答案)
一.选择题(共10小题,满分30分)
1.下列说法正确的是( )
①射线AB与射线BA是同一条射线;
②若线段AB=BC,则B是线段AC的中点;
③线段AB的长度就是点A与点B之间的距离.
A.①②③ B.①③ C.②③ D.③
2.下列运算正确的是( )
A.x2+x2=x4 B.a2 a3=a5
C.(3x)2=6x2 D.(mn)5÷(mn)=mn4
3.若∠A=32°18′,∠B=32°15′30″,∠C=32.25°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
4.在同一平面内,已知∠AOB=60°,∠COB=20°,则∠AOC等于( )
A.80° B.40° C.80°或40° D.20°
5.如图,线段AB的长为1cm,延长AB到C,使BC=2AB,再延长BA到D,使BD=2BC,则线段CD的长为( )
A.10cm B.8cm C.6cm D.12cm
6.已知xy2=﹣2,则﹣xy(x2y5﹣xy3﹣y)的值为( )
A.2 B.6 C.10 D.14
7.如(x+m)与(x+4)的乘积中不含x的一次项,则m的值为( )
A.﹣4 B.4 C.0 D.1
8.如图,点C、O、B在同一条直线上,∠AOB=90°,∠1=∠2,则下列结论:
①∠EOD=90°;②∠3=∠4;③∠2=∠3;④∠2+∠3=90°;其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.若a+b=1,则a2﹣b2+2b的值为( )
A.4 B.3 C.1 D.0
10.已知4y2+my+9是完全平方式,求(6m4﹣8m3)÷(﹣2m2)+3m2的值是( )
A.±48 B.±24 C.48 D.24
二.填空题(共8小题,满分32分)
11.把弯曲的公路改直,就能缩短路程,应用的数学知识是 .
12.若am=3,an=﹣2,则am+n= .
13.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是
14.已知2m﹣3n=﹣5,则代数式m(n﹣4)﹣n(m﹣6)的值为
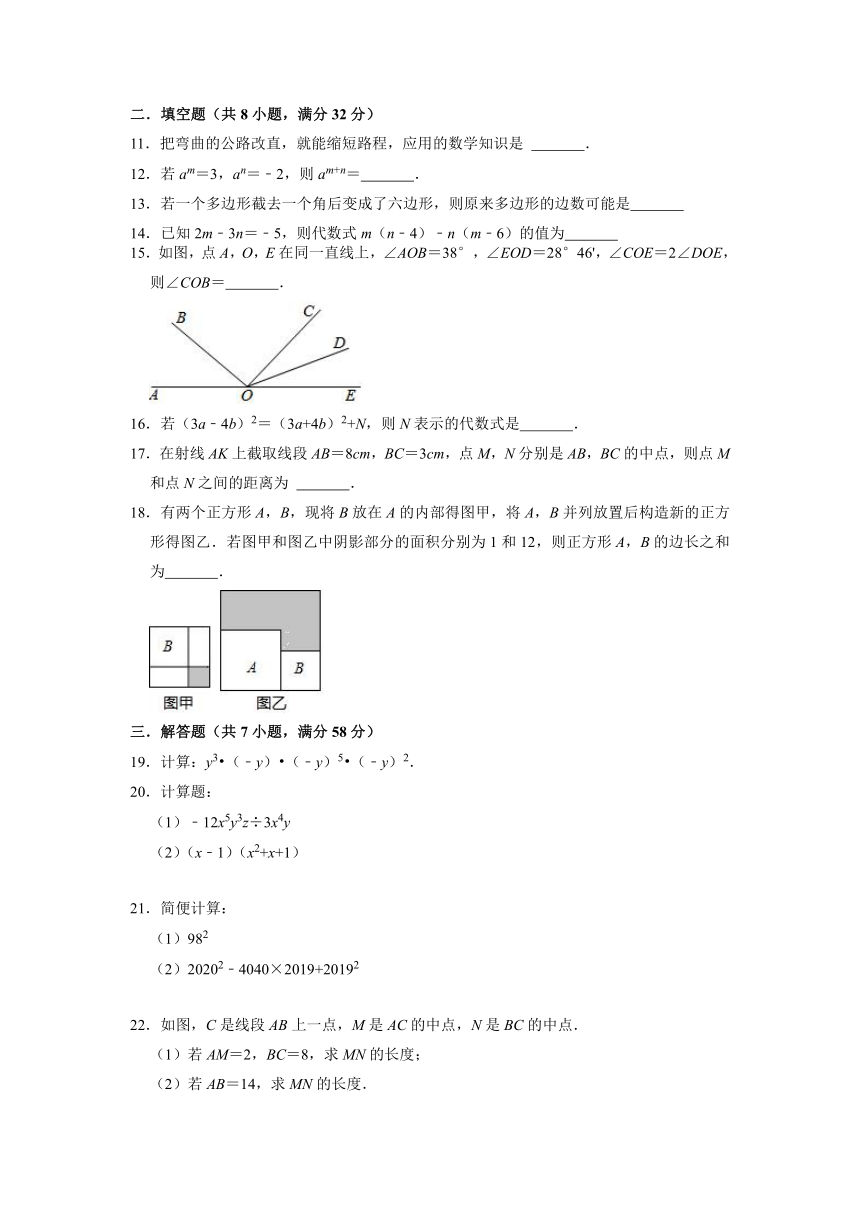
15.如图,点A,O,E在同一直线上,∠AOB=38°,∠EOD=28°46',∠COE=2∠DOE,则∠COB= .
16.若(3a﹣4b)2=(3a+4b)2+N,则N表示的代数式是 .
17.在射线AK上截取线段AB=8cm,BC=3cm,点M,N分别是AB,BC的中点,则点M和点N之间的距离为 .
18.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的边长之和为 .
三.解答题(共7小题,满分58分)
19.计算:y3 (﹣y) (﹣y)5 (﹣y)2.
20.计算题:
(1)﹣12x5y3z÷3x4y
(2)(x﹣1)(x2+x+1)
21.简便计算:
(1)982
(2)20202﹣4040×2019+20192
22.如图,C是线段AB上一点,M是AC的中点,N是BC的中点.
(1)若AM=2,BC=8,求MN的长度;
(2)若AB=14,求MN的长度.
23.如图,已知射线OB,OM,ON在∠AOD内部,OM平分∠AOB,ON平分∠BOD.
(1)若∠AOD=156°,∠DON=48°,求∠MON的度数;
(2)若∠AOD=α°,证明:∠MON=α°.
24.线段与角的计算.
(1)如图1,CE是线段AB上的两点.若AB=6,BC=2,且AE:EC=1:3,求EC的长;
(2)如图2,O为直线AB上一点,且∠COD为直角,OE平分∠BOD,OF平分∠AOE.若∠BOC+∠FOD=117°,求∠BOE的度数.
25.【知识回顾】
七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是:把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.
【理解应用】
(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,求m值;
(2)已知A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,且3A+6B的值与x无关,求y的值;
【能力提升】
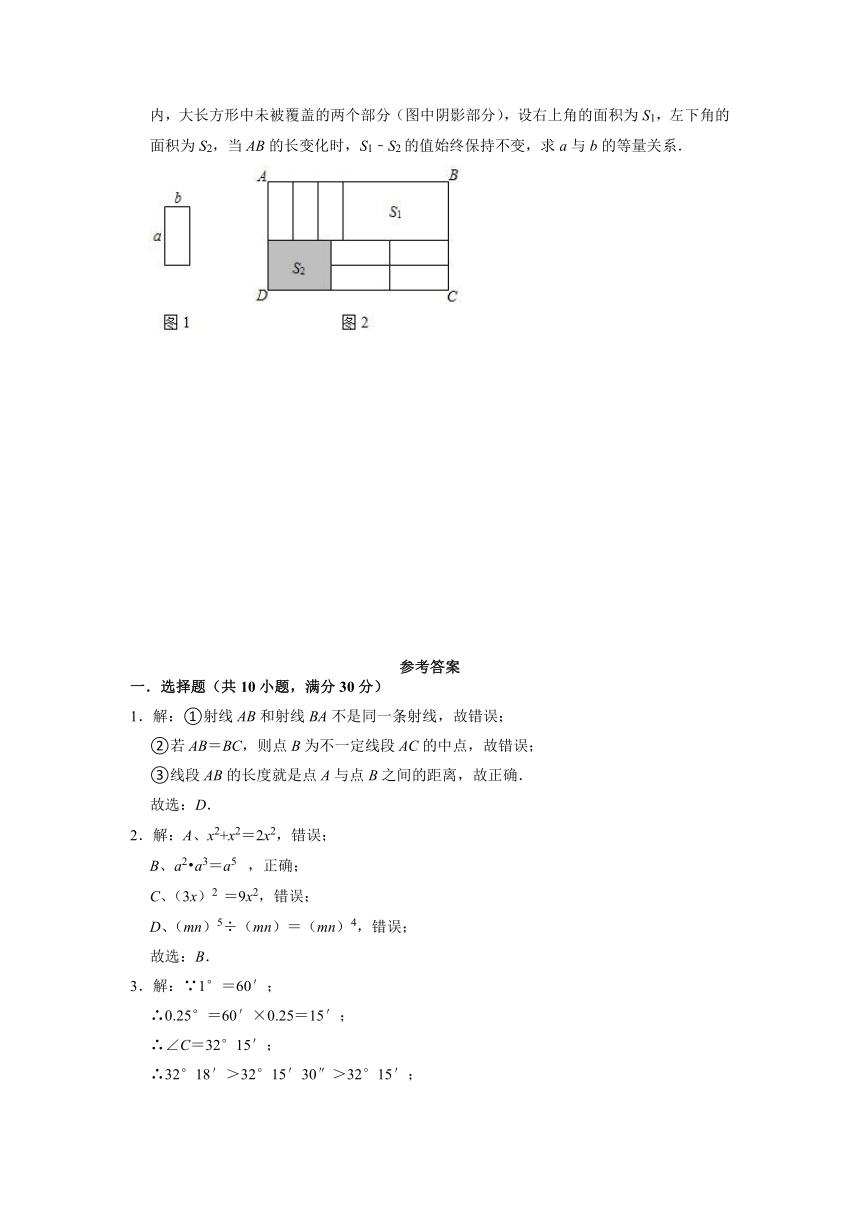
(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
参考答案
一.选择题(共10小题,满分30分)
1.解:①射线AB和射线BA不是同一条射线,故错误;
②若AB=BC,则点B为不一定线段AC的中点,故错误;
③线段AB的长度就是点A与点B之间的距离,故正确.
故选:D.
2.解:A、x2+x2=2x2,错误;
B、a2 a3=a5 ,正确;
C、(3x)2 =9x2,错误;
D、(mn)5÷(mn)=(mn)4,错误;
故选:B.
3.解:∵1°=60′;
∴0.25°=60′×0.25=15′;
∴∠C=32°15′;
∴32°18′>32°15′30″>32°15′;
∴∠A>∠B>∠C.
故选:A.
4.解:当射线OC在∠AOB的内部时,
∠AOC=∠AOB﹣∠COB=60°﹣20°=40°;
当射线OC在∠AOB的外部时,
∠AOC=∠AOB+∠COB=60°+20°=80°;
所以∠AOC的度数为40°或80°,
故选:C.
5.解:∵AB=1cm,
∴BC=2AB=2cm,
∴BD=2BC=4cm,
∴CD=CB+BD=2+4=6cm.
故选:C.
6.解:∵xy2=﹣2,
∴﹣xy(x2y5﹣xy3﹣y)=﹣x3y6+x2y4+xy2=﹣(xy2)3+(xy2)2+xy2=﹣(﹣2)3+(﹣2)2+(﹣2)=8+4﹣2=10;
故选:C.
7.解:(x+m)(x+4)=x2+(m+4)x+4m,
∵乘积中不含x的一次项,
∴m+4=0,
∴m=﹣4.
故选:A.
8.解:∵∠AOB=90°,∠1=∠2,
∴∠2+∠4=90°,
∴∠1+∠4=90°,
即∠EOD=90°,
故①正确,
∵∠1+∠3=90°,
∴∠3=∠4,∠2+∠3=90°,
故②④正确,
∵∠2和∠3大小不确定,
故③不正确,
故选:C.
9.解:∵a+b=1,
∴a2﹣b2+2b=(a+b)(a﹣b)+2b=a﹣b+2b=a+b=1.
故选:C
10.解:(6m4﹣8m3)÷(﹣2m2)+3m2
=﹣3m2+4m+3m2
=4m,
∵4y2+my+9是完全平方式,
∴m=±2×2×3=±12,
当m=12时,原式=4×12=48;
当m=﹣12时,原式=4×(﹣12)=﹣48;
故选:A.
二.填空题(共10小题,满分30分)
11.解:把弯曲的公路改直,就能缩短路程,应用的数学知识是:两点之间线段最短.
故答案为:两点之间线段最短.
12.解:∵am=3,an=﹣2,
∴am+n=am an=3×(﹣2)=﹣6.
故答案为:﹣6
13.解:如图可知,原来多边形的边数可能是5,6,7.
14.解:原式=mn﹣4m﹣mn+6n
=﹣4m+6n
=﹣2(2m﹣3n),
∵2m﹣3n=﹣5,
∴原式=﹣2×(﹣5)=10,
故答案为10.
15.解:∵∠EOD=28°46',∠COE=2∠DOE,
∴∠COE=2×28°46'=57°32',
∴∠COB=180°﹣∠AOB﹣∠COE=180°﹣38°﹣57°32'=84°28'.
故答案为:84°28'.
16.解:已知等式整理得:9a2﹣24ab+16b2=9a2+24ab+16b2+N,
则N=﹣48ab,
故选:D.
17.解:①点C在线段AB上时,如图所示:
∵点M,N分别是AB,BC的中点,
∴AM=BM=AB,
又∵AB=8cm,
∴BM=4cm,
又∵点N是BC的中点,
∴CN=BN=BC,
又∵BC=3cm,
∴BN=1.5cm,
又∵MN=BM﹣BN,
∴MN=4﹣1.5=2.5cm;
②点C在线段AB延长线上时,如图所示:
同理可求出BM=4cm,BN=1.5cm,
又∵MN=BM+BN,
∴MN=4+1.5=5.5cm;
综合所述:MN的长度为2.5cm或5.5cm,
故答案为:2.5cm或5.5cm.
18.解:设正方形A,B的边长分别为a,b.
由题意
由②得到ab=6,
∴(a+b)2=(a﹣b)2+4ab=1+24=25,
∵a+b>0,
∴a+b=5,
故答案为5.
三.解答题(共8小题,满分60分)
19.解:原式=y3 (﹣y) (﹣y)5 y2
=y3 (﹣y) (﹣y5) y2
=y3 y y5 y2
=y3+1+5+2
=y11.
20.解:(1)﹣12x5y3z÷3x4y=﹣4xy2z;
(2)(x﹣1)(x2+x+1)
=x3﹣1.
21.解:(1))982=(100﹣2)2
=1002﹣2×100×2+22
=10000﹣400+4
=9604
(2)20202﹣4040×2019+20192
=20202﹣2×2020×2019+20192
=(2020﹣2019)2
=12
=1.
22.解:(1)∵M是AC的中点,N是BC的中点,
∴MC=AM=2,NC=BC=4,
∴MN=MC+NC=6;故MN的长度为6.
(2)∵M是AC的中点,N是BC的中点,
∴MC=AC,NC=BC,
∴MN=MC+NC==AC+BC=AB=7.故MN的长度为7.
23.(1)解:∵OM平分∠AOB,ON平分∠BOD,
∴∠NOB=∠DOB,∠BOM=∠BOA,
∴∠NOB+∠BOM=∠DOB+∠BOA=(∠DOB+∠BOA)
∴∠MON=∠AOD,
又∵∠AOD=156°,
∴∠MON=×156°=78°;
(2)证明:由(1)知,∠MON=∠AOD,
∵∠AOD=α°,
∴∠MON=α°.
24.解:(1)∵AB=6,BC=2,
∴AC=6﹣2=4,
∵AE:EC=1:3,
∴EC==3;
(2)设∠BOE=x°,
∵∠COD为直角,OE平分∠BOD,
∴∠DOE=∠BOE=x,∠BOC=90﹣2x,
∵OF平分∠AOE,而∠AOE=180﹣x,
∴∠FOD=∠FOE﹣∠DOE=(180﹣x)﹣x,
∴(90﹣2x)+(180﹣x)﹣x=117,
解得x=18,
所以∠BOE的度数是18°.
25.解:(1)(2x﹣3)m+2m2﹣3x
=2mx﹣3m+2m2﹣3x
=(2m﹣3)x+2m2﹣3m,
∵其值与x的取值无关,
∴2m﹣3=0,
解得,m=,
答:当m=时,多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关;
(2)∵A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,
∴3A+6B=3[(2x+1)(x﹣1)﹣x(1﹣3y)]+6(﹣x2+xy﹣1)
=3(2x2﹣2x+x﹣1﹣x+3xy]﹣6x2+6xy﹣6
=6x2﹣6x+3x﹣3﹣3x+9xy﹣6x2+6xy﹣6
=15xy﹣6x﹣9
=3x(5y﹣2)﹣9,
∵3A+6B的值与x无关,
∴5y﹣2=0,即y=;
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2=a(x﹣3b)﹣2b(x﹣2a)=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变.
∴S1﹣S2取值与x无关,
∴a﹣2b=0
∴a=2b.
一.选择题(共10小题,满分30分)
1.下列说法正确的是( )
①射线AB与射线BA是同一条射线;
②若线段AB=BC,则B是线段AC的中点;
③线段AB的长度就是点A与点B之间的距离.
A.①②③ B.①③ C.②③ D.③
2.下列运算正确的是( )
A.x2+x2=x4 B.a2 a3=a5
C.(3x)2=6x2 D.(mn)5÷(mn)=mn4
3.若∠A=32°18′,∠B=32°15′30″,∠C=32.25°,则( )
A.∠A>∠B>∠C B.∠B>∠A>∠C
C.∠A>∠C>∠B D.∠C>∠A>∠B
4.在同一平面内,已知∠AOB=60°,∠COB=20°,则∠AOC等于( )
A.80° B.40° C.80°或40° D.20°
5.如图,线段AB的长为1cm,延长AB到C,使BC=2AB,再延长BA到D,使BD=2BC,则线段CD的长为( )
A.10cm B.8cm C.6cm D.12cm
6.已知xy2=﹣2,则﹣xy(x2y5﹣xy3﹣y)的值为( )
A.2 B.6 C.10 D.14
7.如(x+m)与(x+4)的乘积中不含x的一次项,则m的值为( )
A.﹣4 B.4 C.0 D.1
8.如图,点C、O、B在同一条直线上,∠AOB=90°,∠1=∠2,则下列结论:
①∠EOD=90°;②∠3=∠4;③∠2=∠3;④∠2+∠3=90°;其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
9.若a+b=1,则a2﹣b2+2b的值为( )
A.4 B.3 C.1 D.0
10.已知4y2+my+9是完全平方式,求(6m4﹣8m3)÷(﹣2m2)+3m2的值是( )
A.±48 B.±24 C.48 D.24
二.填空题(共8小题,满分32分)
11.把弯曲的公路改直,就能缩短路程,应用的数学知识是 .
12.若am=3,an=﹣2,则am+n= .
13.若一个多边形截去一个角后变成了六边形,则原来多边形的边数可能是
14.已知2m﹣3n=﹣5,则代数式m(n﹣4)﹣n(m﹣6)的值为
15.如图,点A,O,E在同一直线上,∠AOB=38°,∠EOD=28°46',∠COE=2∠DOE,则∠COB= .
16.若(3a﹣4b)2=(3a+4b)2+N,则N表示的代数式是 .
17.在射线AK上截取线段AB=8cm,BC=3cm,点M,N分别是AB,BC的中点,则点M和点N之间的距离为 .
18.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的边长之和为 .
三.解答题(共7小题,满分58分)
19.计算:y3 (﹣y) (﹣y)5 (﹣y)2.
20.计算题:
(1)﹣12x5y3z÷3x4y
(2)(x﹣1)(x2+x+1)
21.简便计算:
(1)982
(2)20202﹣4040×2019+20192
22.如图,C是线段AB上一点,M是AC的中点,N是BC的中点.
(1)若AM=2,BC=8,求MN的长度;
(2)若AB=14,求MN的长度.
23.如图,已知射线OB,OM,ON在∠AOD内部,OM平分∠AOB,ON平分∠BOD.
(1)若∠AOD=156°,∠DON=48°,求∠MON的度数;
(2)若∠AOD=α°,证明:∠MON=α°.
24.线段与角的计算.
(1)如图1,CE是线段AB上的两点.若AB=6,BC=2,且AE:EC=1:3,求EC的长;
(2)如图2,O为直线AB上一点,且∠COD为直角,OE平分∠BOD,OF平分∠AOE.若∠BOC+∠FOD=117°,求∠BOE的度数.
25.【知识回顾】
七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是:把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.
【理解应用】
(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,求m值;
(2)已知A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,且3A+6B的值与x无关,求y的值;
【能力提升】
(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.
参考答案
一.选择题(共10小题,满分30分)
1.解:①射线AB和射线BA不是同一条射线,故错误;
②若AB=BC,则点B为不一定线段AC的中点,故错误;
③线段AB的长度就是点A与点B之间的距离,故正确.
故选:D.
2.解:A、x2+x2=2x2,错误;
B、a2 a3=a5 ,正确;
C、(3x)2 =9x2,错误;
D、(mn)5÷(mn)=(mn)4,错误;
故选:B.
3.解:∵1°=60′;
∴0.25°=60′×0.25=15′;
∴∠C=32°15′;
∴32°18′>32°15′30″>32°15′;
∴∠A>∠B>∠C.
故选:A.
4.解:当射线OC在∠AOB的内部时,
∠AOC=∠AOB﹣∠COB=60°﹣20°=40°;
当射线OC在∠AOB的外部时,
∠AOC=∠AOB+∠COB=60°+20°=80°;
所以∠AOC的度数为40°或80°,
故选:C.
5.解:∵AB=1cm,
∴BC=2AB=2cm,
∴BD=2BC=4cm,
∴CD=CB+BD=2+4=6cm.
故选:C.
6.解:∵xy2=﹣2,
∴﹣xy(x2y5﹣xy3﹣y)=﹣x3y6+x2y4+xy2=﹣(xy2)3+(xy2)2+xy2=﹣(﹣2)3+(﹣2)2+(﹣2)=8+4﹣2=10;
故选:C.
7.解:(x+m)(x+4)=x2+(m+4)x+4m,
∵乘积中不含x的一次项,
∴m+4=0,
∴m=﹣4.
故选:A.
8.解:∵∠AOB=90°,∠1=∠2,
∴∠2+∠4=90°,
∴∠1+∠4=90°,
即∠EOD=90°,
故①正确,
∵∠1+∠3=90°,
∴∠3=∠4,∠2+∠3=90°,
故②④正确,
∵∠2和∠3大小不确定,
故③不正确,
故选:C.
9.解:∵a+b=1,
∴a2﹣b2+2b=(a+b)(a﹣b)+2b=a﹣b+2b=a+b=1.
故选:C
10.解:(6m4﹣8m3)÷(﹣2m2)+3m2
=﹣3m2+4m+3m2
=4m,
∵4y2+my+9是完全平方式,
∴m=±2×2×3=±12,
当m=12时,原式=4×12=48;
当m=﹣12时,原式=4×(﹣12)=﹣48;
故选:A.
二.填空题(共10小题,满分30分)
11.解:把弯曲的公路改直,就能缩短路程,应用的数学知识是:两点之间线段最短.
故答案为:两点之间线段最短.
12.解:∵am=3,an=﹣2,
∴am+n=am an=3×(﹣2)=﹣6.
故答案为:﹣6
13.解:如图可知,原来多边形的边数可能是5,6,7.
14.解:原式=mn﹣4m﹣mn+6n
=﹣4m+6n
=﹣2(2m﹣3n),
∵2m﹣3n=﹣5,
∴原式=﹣2×(﹣5)=10,
故答案为10.
15.解:∵∠EOD=28°46',∠COE=2∠DOE,
∴∠COE=2×28°46'=57°32',
∴∠COB=180°﹣∠AOB﹣∠COE=180°﹣38°﹣57°32'=84°28'.
故答案为:84°28'.
16.解:已知等式整理得:9a2﹣24ab+16b2=9a2+24ab+16b2+N,
则N=﹣48ab,
故选:D.
17.解:①点C在线段AB上时,如图所示:
∵点M,N分别是AB,BC的中点,
∴AM=BM=AB,
又∵AB=8cm,
∴BM=4cm,
又∵点N是BC的中点,
∴CN=BN=BC,
又∵BC=3cm,
∴BN=1.5cm,
又∵MN=BM﹣BN,
∴MN=4﹣1.5=2.5cm;
②点C在线段AB延长线上时,如图所示:
同理可求出BM=4cm,BN=1.5cm,
又∵MN=BM+BN,
∴MN=4+1.5=5.5cm;
综合所述:MN的长度为2.5cm或5.5cm,
故答案为:2.5cm或5.5cm.
18.解:设正方形A,B的边长分别为a,b.
由题意
由②得到ab=6,
∴(a+b)2=(a﹣b)2+4ab=1+24=25,
∵a+b>0,
∴a+b=5,
故答案为5.
三.解答题(共8小题,满分60分)
19.解:原式=y3 (﹣y) (﹣y)5 y2
=y3 (﹣y) (﹣y5) y2
=y3 y y5 y2
=y3+1+5+2
=y11.
20.解:(1)﹣12x5y3z÷3x4y=﹣4xy2z;
(2)(x﹣1)(x2+x+1)
=x3﹣1.
21.解:(1))982=(100﹣2)2
=1002﹣2×100×2+22
=10000﹣400+4
=9604
(2)20202﹣4040×2019+20192
=20202﹣2×2020×2019+20192
=(2020﹣2019)2
=12
=1.
22.解:(1)∵M是AC的中点,N是BC的中点,
∴MC=AM=2,NC=BC=4,
∴MN=MC+NC=6;故MN的长度为6.
(2)∵M是AC的中点,N是BC的中点,
∴MC=AC,NC=BC,
∴MN=MC+NC==AC+BC=AB=7.故MN的长度为7.
23.(1)解:∵OM平分∠AOB,ON平分∠BOD,
∴∠NOB=∠DOB,∠BOM=∠BOA,
∴∠NOB+∠BOM=∠DOB+∠BOA=(∠DOB+∠BOA)
∴∠MON=∠AOD,
又∵∠AOD=156°,
∴∠MON=×156°=78°;
(2)证明:由(1)知,∠MON=∠AOD,
∵∠AOD=α°,
∴∠MON=α°.
24.解:(1)∵AB=6,BC=2,
∴AC=6﹣2=4,
∵AE:EC=1:3,
∴EC==3;
(2)设∠BOE=x°,
∵∠COD为直角,OE平分∠BOD,
∴∠DOE=∠BOE=x,∠BOC=90﹣2x,
∵OF平分∠AOE,而∠AOE=180﹣x,
∴∠FOD=∠FOE﹣∠DOE=(180﹣x)﹣x,
∴(90﹣2x)+(180﹣x)﹣x=117,
解得x=18,
所以∠BOE的度数是18°.
25.解:(1)(2x﹣3)m+2m2﹣3x
=2mx﹣3m+2m2﹣3x
=(2m﹣3)x+2m2﹣3m,
∵其值与x的取值无关,
∴2m﹣3=0,
解得,m=,
答:当m=时,多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关;
(2)∵A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,
∴3A+6B=3[(2x+1)(x﹣1)﹣x(1﹣3y)]+6(﹣x2+xy﹣1)
=3(2x2﹣2x+x﹣1﹣x+3xy]﹣6x2+6xy﹣6
=6x2﹣6x+3x﹣3﹣3x+9xy﹣6x2+6xy﹣6
=15xy﹣6x﹣9
=3x(5y﹣2)﹣9,
∵3A+6B的值与x无关,
∴5y﹣2=0,即y=;
(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),
∴S1﹣S2=a(x﹣3b)﹣2b(x﹣2a)=(a﹣2b)x+ab,
∵当AB的长变化时,S1﹣S2的值始终保持不变.
∴S1﹣S2取值与x无关,
∴a﹣2b=0
∴a=2b.
同课章节目录
