沪科版数学七年级下册 7.3 一元一次不等式组 课件(共22张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 7.3 一元一次不等式组 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 18:24:30 | ||
图片预览







文档简介
(共22张PPT)
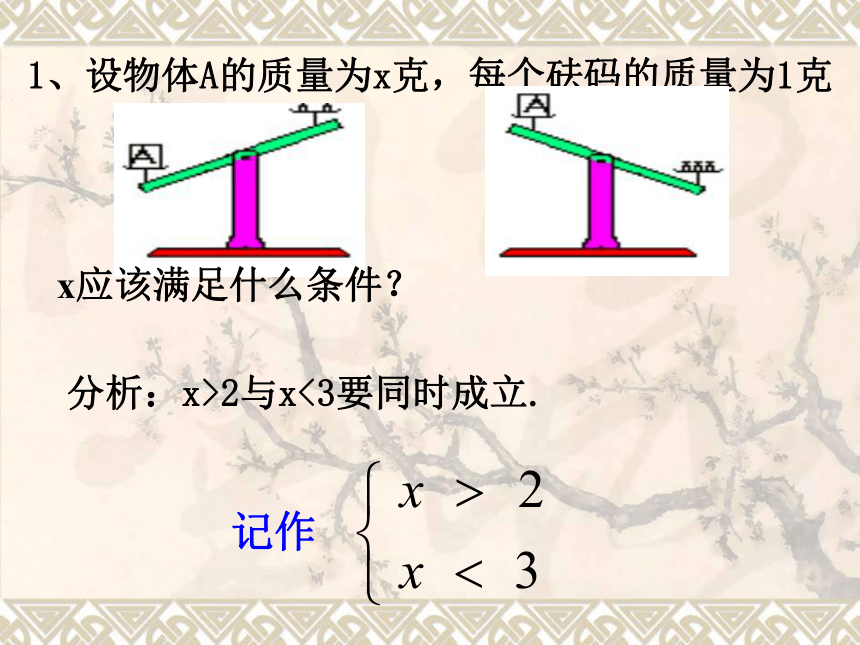
1、设物体A的质量为x克,每个砝码的质量为1克
x应该满足什么条件?
分析:x>2与x<3要同时成立.
记作
2、一群猴子分100个桃子,如果每只猴子9个有剩余,如果每只猴子10个不够分,若有x只猴子,x应满足什么条件?
分析:9x<100和10x>100同时成立.
记作:
观察上面得到的两组式子有什么共同点
一元一次不等式组的概念 :
由几个含有同一个未知数的一元一次不等
式组成的不等式组,叫做一元一次不等式组.
判断下列不等式组是否为一元一次不等式组,若不是说明理由.
①
②
③
④
⑤
⑥
①
②
在同一数轴上表示不等
式①,②的解集:
①,②的解集的公共部分记作: 22
3
0
1
如何找一元一次不等式组的解集呢?
一元一次不等式组中几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集。
①
②
则 2的解集
求一元一次不等式组解集的过程,叫做解不等式组。
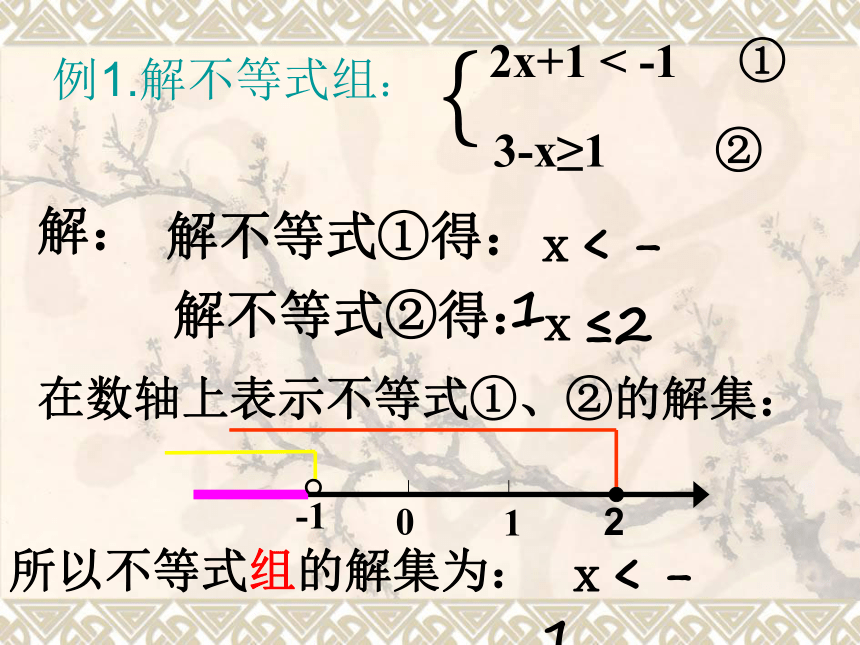
2x+1 < -1 ①
3-x≥1 ②
{
解不等式①得:
x< -1
解不等式②得:
x≤2
在数轴上表示不等式①、②的解集:
例1.解不等式组:
解:
-1
所以不等式组的解集为:
x< -1
2
0
1
-5
-2
0
-3
-1
-4
例2. 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解
集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
同大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
例2. 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
同小取小
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
例2. 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小,小大中间找
例2. 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大,小小无解了
比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 同大取大,
2.同小取小;
3.大小小大中间找,
4.大大小小无解了.
x>-2
x<-4
-1无解
归纳 解一元一次不等式组的一般步骤:
2.(1)利用数轴找几个解集的公共部分:
(2)利用规律: 同大取大,同小取小;大小小大中间找,大大小小无解了。
1.求出不等式组中各个不等式的解集;
3.写出这个不等式组的解集;
练习:解不等式组:
1、
2、
3、求不等式组
的整数解。
4、试求问题2中的x值.
2、一群猴子分100个桃子,如果每只猴子9个有剩余,如果每只猴子10个不够分,若有x只猴子,x应满足什么条件?
解:
解得:
由题意得x为整数,
所以
1.关键概念:
一元一次不等式组;不等式组的解集.
2.解不等式组的方法步骤
作业:
1、习题7.3
2、同步练习(一)(二)
学习快乐!
1、设物体A的质量为x克,每个砝码的质量为1克
x应该满足什么条件?
分析:x>2与x<3要同时成立.
记作
2、一群猴子分100个桃子,如果每只猴子9个有剩余,如果每只猴子10个不够分,若有x只猴子,x应满足什么条件?
分析:9x<100和10x>100同时成立.
记作:
观察上面得到的两组式子有什么共同点
一元一次不等式组的概念 :
由几个含有同一个未知数的一元一次不等
式组成的不等式组,叫做一元一次不等式组.
判断下列不等式组是否为一元一次不等式组,若不是说明理由.
①
②
③
④
⑤
⑥
①
②
在同一数轴上表示不等
式①,②的解集:
①,②的解集的公共部分记作: 2
3
0
1
如何找一元一次不等式组的解集呢?
一元一次不等式组中几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集。
①
②
则 2
求一元一次不等式组解集的过程,叫做解不等式组。
2x+1 < -1 ①
3-x≥1 ②
{
解不等式①得:
x< -1
解不等式②得:
x≤2
在数轴上表示不等式①、②的解集:
例1.解不等式组:
解:
-1
所以不等式组的解集为:
x< -1
2
0
1
-5
-2
0
-3
-1
-4
例2. 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
-5
-2
0
-3
-1
2
1
-4
解:原不等式组的解
集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
同大取大
-5
-2
0
-3
-1
1
-4
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
-3
-1
-4
0
-7
-6
例2. 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
同小取小
-5
-2
0
-3
-1
1
-4
-6
-5
-2
-3
-1
-4
0
-7
-6
例2. 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-3
-2
-1
0
4
2
1
3
5
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
解:原不等式组的解集为
大小,小大中间找
例2. 求下列不等式组的解集:
0
7
6
5
4
2
1
3
8
9
-5
-2
-3
-1
-4
0
-7
-6
-3
-2
-1
0
4
2
1
3
5
-5
-2
0
-3
-1
1
-4
-6
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
解:原不等式组无解.
大大,小小无解了
比一比:看谁反应快
运用规律求下列不等式组的解集:
1. 同大取大,
2.同小取小;
3.大小小大中间找,
4.大大小小无解了.
x>-2
x<-4
-1
归纳 解一元一次不等式组的一般步骤:
2.(1)利用数轴找几个解集的公共部分:
(2)利用规律: 同大取大,同小取小;大小小大中间找,大大小小无解了。
1.求出不等式组中各个不等式的解集;
3.写出这个不等式组的解集;
练习:解不等式组:
1、
2、
3、求不等式组
的整数解。
4、试求问题2中的x值.
2、一群猴子分100个桃子,如果每只猴子9个有剩余,如果每只猴子10个不够分,若有x只猴子,x应满足什么条件?
解:
解得:
由题意得x为整数,
所以
1.关键概念:
一元一次不等式组;不等式组的解集.
2.解不等式组的方法步骤
作业:
1、习题7.3
2、同步练习(一)(二)
学习快乐!
