沪科版数学七年级下册 8.2 多项式与多项式相乘 课件(共18张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 8.2 多项式与多项式相乘 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 111.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
多项式与多项式相乘
整式乘法
回顾 & 思考
② 再把所得的积相加。
如何进行单项式与多项式乘法的运算?
① 用单项式分别去乘多项式的每一项,
进行单项式与多项式乘法运算时,要注意一些什么?
单项式乘以多项式的 依据是 ;
乘法对加法的分配律
① 不能漏乘:
即单项式要乘遍多项式的每一项。
② 去括号时注意符号的确定。
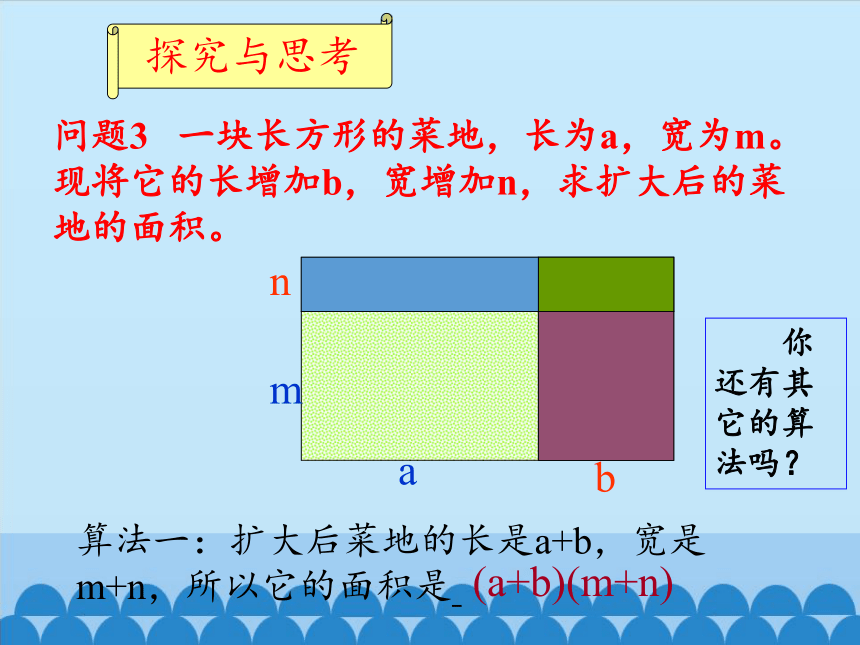
问题3 一块长方形的菜地,长为a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
n
b
m
a
(a+b)(m+n)
算法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是
你还有其它的算法吗?
探究与思考
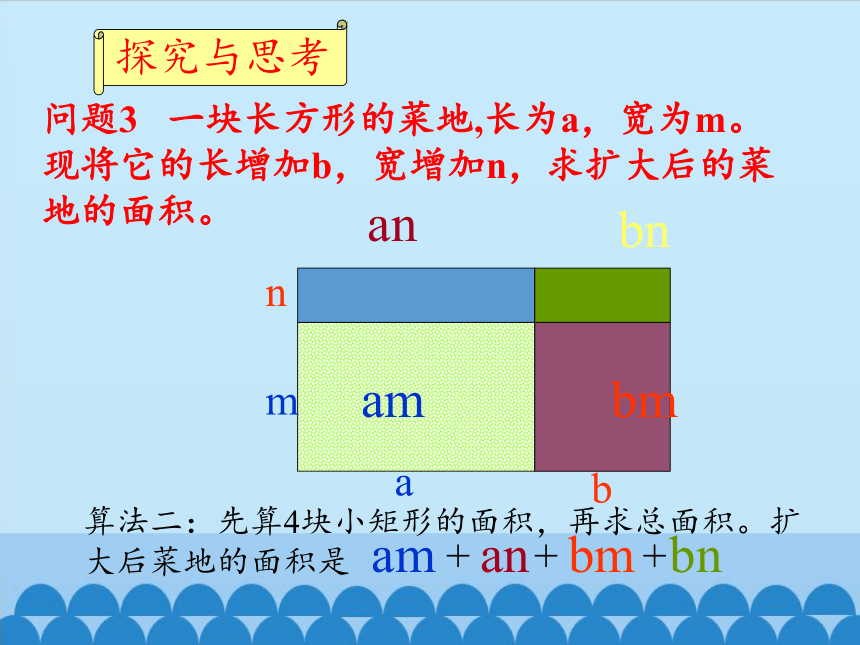
问题3 一块长方形的菜地,长为a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
m
a
am
n
an
b
bm
bn
am
an
bm
bn
+
+
+
算法二:先算4块小矩形的面积,再求总面积。扩大后菜地的面积是
探究与思考
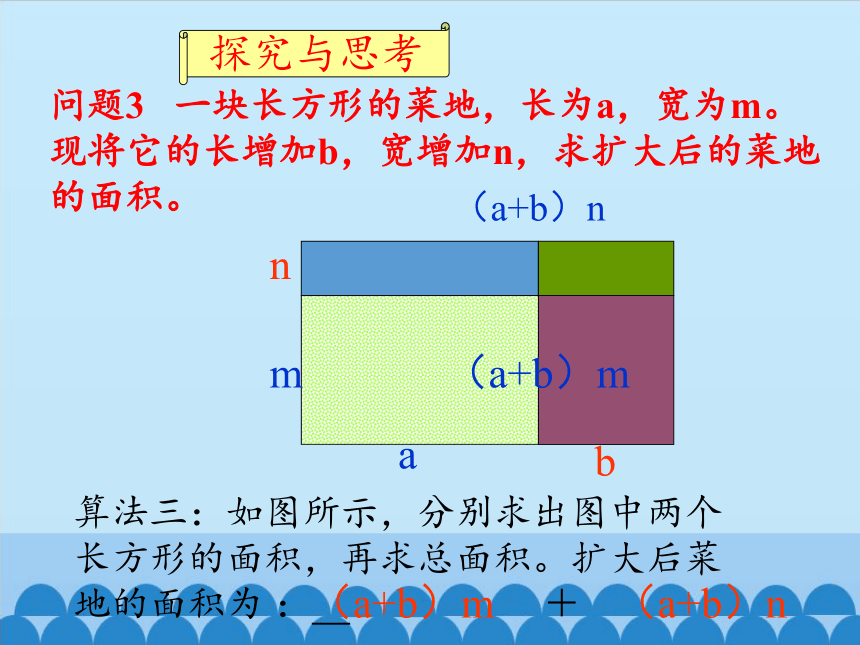
问题3 一块长方形的菜地,长为a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
b
m
a
n
算法三:如图所示,分别求出图中两个长方形的面积,再求总面积。扩大后菜地的面积为 :
(a+b)m
(a+b)m
(a+b)n
(a+b)n
+
探究与思考
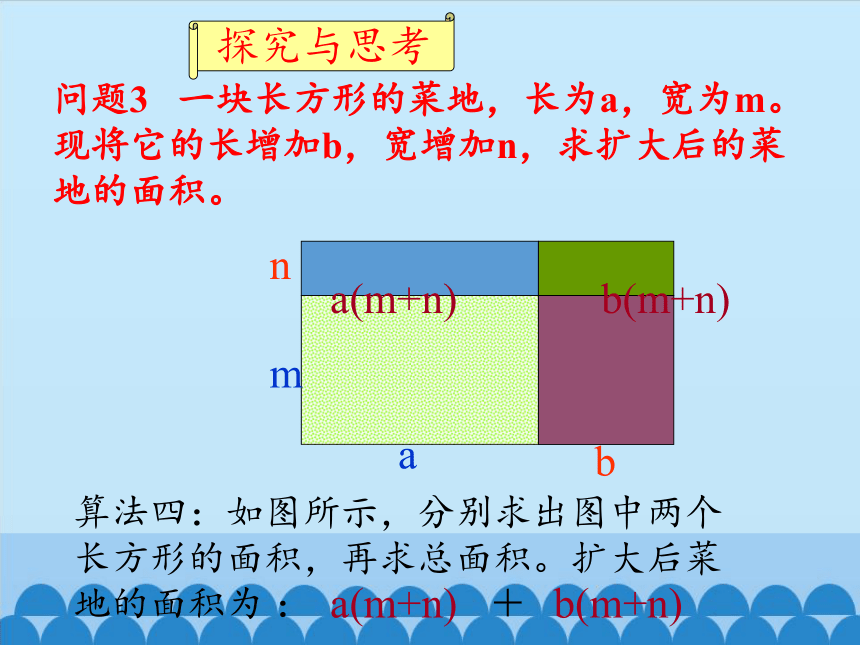
问题3 一块长方形的菜地,长为a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
n
m
a
b
算法四:如图所示,分别求出图中两个长方形的面积,再求总面积。扩大后菜地的面积为 :
a(m+n)
b(m+n)
a(m+n)
b(m+n)
+
探究与思考
观察这几个式子:
(a+b)(m+n)
am+an+bm+bn
(a+b)m+(a+b)n
a(m+n)+b(m+n)
你能说出它们有何关系吗?
分析与比较
可以发现:
(a+b)(m+n)
am+an+bm+bn
(a+b)m+(a+b)n
a(m+n)+b(m+n)
由此你能得到什么启发?
=
=
=
分析与比较
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
你会说吗?
1.运用多项式的乘法法则时,必须做到不重不漏。
2.多项式与多项式相乘,仍得多项式。
3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”。
4.多项式与多项式相乘的展开式中,有同类项要合并同类项。
温馨提示
(1)(ax+b)(cx+d);
(2)(–2x – 1)(3x – 2);
例 6 计算:
跟我学
跟我学
例7 计算:
(a+b)(a2-ab+b2);
(y2+y+1)(y+2)
小试牛刀
(补充 )计算:
(2) (3x-5)(2x+3)-(2x-1)(x+1)
(1) (3a–2)(a–1) +(a+1)(a+2);
想挑战吗?
比一比,看谁算得又快又准:
(1)(2n+6)(n-3);
(2)(3x-y)(3x+y);
(3)(3a-2)(a-1)+(a+1)(a+2);
(4)(3a+2)(3a–2)–9a(a-1)。
回顾交流:
本节课我们学习了那些内容?
多项式乘以多项式的依据是什么?
如何进行多项式与多项式乘法运算?
谢 谢
多项式与多项式相乘
整式乘法
回顾 & 思考
② 再把所得的积相加。
如何进行单项式与多项式乘法的运算?
① 用单项式分别去乘多项式的每一项,
进行单项式与多项式乘法运算时,要注意一些什么?
单项式乘以多项式的 依据是 ;
乘法对加法的分配律
① 不能漏乘:
即单项式要乘遍多项式的每一项。
② 去括号时注意符号的确定。
问题3 一块长方形的菜地,长为a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
n
b
m
a
(a+b)(m+n)
算法一:扩大后菜地的长是a+b,宽是m+n,所以它的面积是
你还有其它的算法吗?
探究与思考
问题3 一块长方形的菜地,长为a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
m
a
am
n
an
b
bm
bn
am
an
bm
bn
+
+
+
算法二:先算4块小矩形的面积,再求总面积。扩大后菜地的面积是
探究与思考
问题3 一块长方形的菜地,长为a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
b
m
a
n
算法三:如图所示,分别求出图中两个长方形的面积,再求总面积。扩大后菜地的面积为 :
(a+b)m
(a+b)m
(a+b)n
(a+b)n
+
探究与思考
问题3 一块长方形的菜地,长为a,宽为m。现将它的长增加b,宽增加n,求扩大后的菜地的面积。
n
m
a
b
算法四:如图所示,分别求出图中两个长方形的面积,再求总面积。扩大后菜地的面积为 :
a(m+n)
b(m+n)
a(m+n)
b(m+n)
+
探究与思考
观察这几个式子:
(a+b)(m+n)
am+an+bm+bn
(a+b)m+(a+b)n
a(m+n)+b(m+n)
你能说出它们有何关系吗?
分析与比较
可以发现:
(a+b)(m+n)
am+an+bm+bn
(a+b)m+(a+b)n
a(m+n)+b(m+n)
由此你能得到什么启发?
=
=
=
分析与比较
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+an
+bm
+bn
多项式的乘法法则
多项式与多项式相乘,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
你会说吗?
1.运用多项式的乘法法则时,必须做到不重不漏。
2.多项式与多项式相乘,仍得多项式。
3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”。
4.多项式与多项式相乘的展开式中,有同类项要合并同类项。
温馨提示
(1)(ax+b)(cx+d);
(2)(–2x – 1)(3x – 2);
例 6 计算:
跟我学
跟我学
例7 计算:
(a+b)(a2-ab+b2);
(y2+y+1)(y+2)
小试牛刀
(补充 )计算:
(2) (3x-5)(2x+3)-(2x-1)(x+1)
(1) (3a–2)(a–1) +(a+1)(a+2);
想挑战吗?
比一比,看谁算得又快又准:
(1)(2n+6)(n-3);
(2)(3x-y)(3x+y);
(3)(3a-2)(a-1)+(a+1)(a+2);
(4)(3a+2)(3a–2)–9a(a-1)。
回顾交流:
本节课我们学习了那些内容?
多项式乘以多项式的依据是什么?
如何进行多项式与多项式乘法运算?
谢 谢
