沪科版数学七年级下册 10.1 相交线 课件(共22张PPT)
文档属性
| 名称 | 沪科版数学七年级下册 10.1 相交线 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 161.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 18:03:33 | ||
图片预览







文档简介
(共22张PPT)
10.1 相交线
10.1相交线
(1)邻补角、对顶角
第十章 相交线与平行线
学前准备:
填空:
①两个角的和 ,这样的两个角叫做互为补角,即其中一个角是另一个角的补角。
②同角或 的补角 。
等于一个平角
等角
相等
探索与思考:
邻补角、对顶角
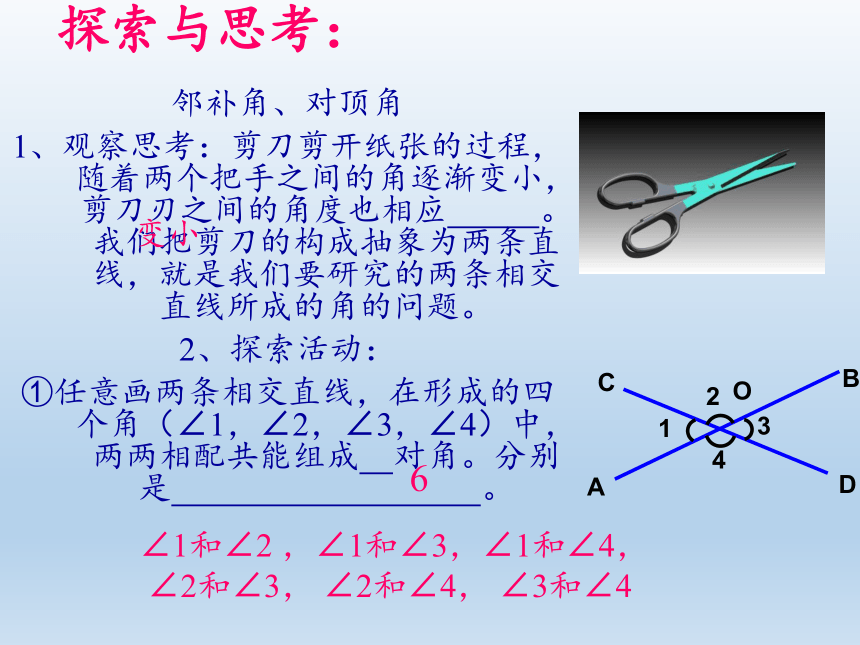
1、观察思考:剪刀剪开纸张的过程,随着两个把手之间的角逐渐变小,剪刀刃之间的角度也相应 。我们把剪刀的构成抽象为两条直线,就是我们要研究的两条相交直线所成的角的问题。
2、探索活动:
①任意画两条相交直线,在形成的四个角(∠1,∠2,∠3,∠4)中,两两相配共能组成 对角。分别是 。
B
A
C
D
O
1
2
3
4
变小
∠1和∠2 ,∠1和∠3,∠1和∠4,
∠2和∠3, ∠2和∠4, ∠3和∠4
6
B
A
C
D
O
1
2
3
4
数量关系
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
1
2
1
3
互补
相等
A
B
C
D
)
(
1
3
4
2
)
(
A
B
C
D
)
(
1
3
4
2
)
(
邻补角:两个角有公共顶点有一条公共边,它们的另一边互为反向延长线,这两个角互为邻补角。
对顶角:两个角有公共顶
点且一个角的两边是另
一个角的两边的反向延
长线,这两个角互为对顶角。
定义:
结论:
①两条直线相交所构成的四个角中,邻补角有 对。对顶角有 对。
②形成的前提条件是两条直线相交。
4
2
性质:
1、邻补角的性质:邻补角 。
注意:邻补角是互补的一种特殊的情况,数量上 ,位置上有一条 。
互补
互补
公共边
性质:
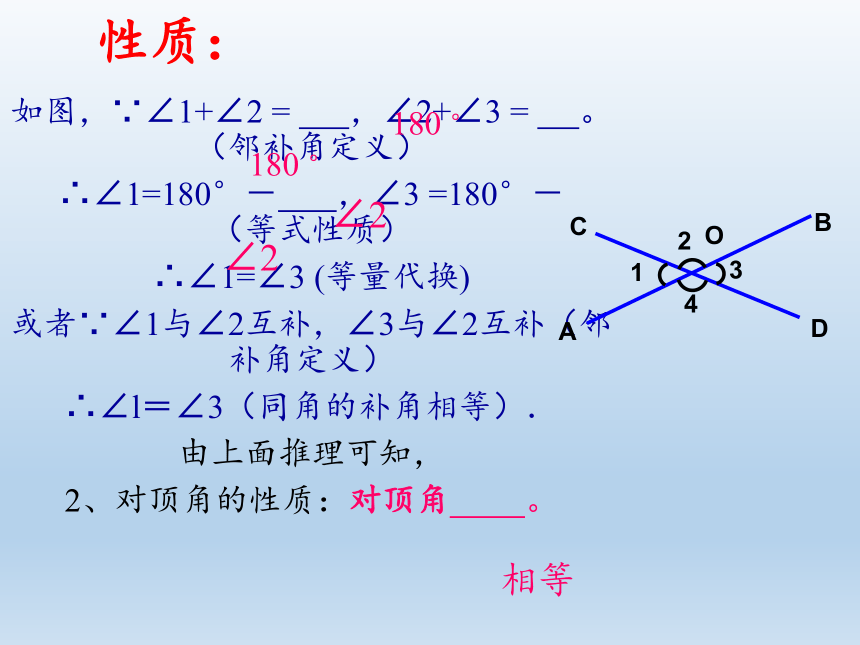
如图,∵∠1+∠2 = ,∠2+∠3 = 。(邻补角定义)
∴∠1=180°- ,∠3 =180°- (等式性质)
∴∠1=∠3 (等量代换)
或者∵∠1与∠2互补,∠3与∠2互补(邻补角定义)
∴∠l=∠3(同角的补角相等).
由上面推理可知,
2、对顶角的性质:对顶角 。
B
A
C
D
O
1
2
3
4
180 °
180 °
∠2
∠2
相等
应用:
例 1. 如图,已知直线a、b相交。∠1=40°,求∠2、∠3、∠4的度数
解:
∵∠3=∠1=40°( )。
∴∠2=180°-∠1=180°-40°=140° ( )。
∴∠4=∠2=140°( )。
对顶角相等
邻补角定义
对顶角相等
收获:
1、两条直线相交所得的四个角中,有一个公共顶点,没有公共边的两个角叫做对顶角。不仅有一个公共顶点,还有一条公共边的两个角叫做邻补角。
2、数量关系是邻补角互补,对顶角相等。
3、用对顶角和邻补角的性质进行简单的推理和证明。
自我检测:
(一)选择题:
1、如图所示,∠1和∠2是对顶角的图形有( )
A.1个 B.2个 C.3个 D.4个
A
2、如图(1)所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
(1)
B
3、下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
B
4、如图(2)所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A.62° B.118° C.72° D.59°
(2)
A
(二)填空题:
1、如图(3)所示,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
2、如图(3)所示,若∠1=25°,则∠2=______,∠3=______,∠4=_____.
(3)
∠2或∠4
∠3
155 °
25 °
155 °
3、如图(4)所示,直线AB,CD相交于点O,若∠1-∠2=70 °,则∠BOD=_____,∠2=____.
(4)
125 °
55 °
六、拓展延伸:
1、如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
b c
a
1
2
3
4
2、如图所示, 直线AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的 度数.
C
A
E O B
D
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
性质
邻补角互补
对顶角相等
相同点
都有一个公共顶点,它们都是成对出现的
不同点
对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个
知识回顾:
课本P121 习题1 , 2
作业
谢 谢
10.1 相交线
10.1相交线
(1)邻补角、对顶角
第十章 相交线与平行线
学前准备:
填空:
①两个角的和 ,这样的两个角叫做互为补角,即其中一个角是另一个角的补角。
②同角或 的补角 。
等于一个平角
等角
相等
探索与思考:
邻补角、对顶角
1、观察思考:剪刀剪开纸张的过程,随着两个把手之间的角逐渐变小,剪刀刃之间的角度也相应 。我们把剪刀的构成抽象为两条直线,就是我们要研究的两条相交直线所成的角的问题。
2、探索活动:
①任意画两条相交直线,在形成的四个角(∠1,∠2,∠3,∠4)中,两两相配共能组成 对角。分别是 。
B
A
C
D
O
1
2
3
4
变小
∠1和∠2 ,∠1和∠3,∠1和∠4,
∠2和∠3, ∠2和∠4, ∠3和∠4
6
B
A
C
D
O
1
2
3
4
数量关系
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
1
2
1
3
互补
相等
A
B
C
D
)
(
1
3
4
2
)
(
A
B
C
D
)
(
1
3
4
2
)
(
邻补角:两个角有公共顶点有一条公共边,它们的另一边互为反向延长线,这两个角互为邻补角。
对顶角:两个角有公共顶
点且一个角的两边是另
一个角的两边的反向延
长线,这两个角互为对顶角。
定义:
结论:
①两条直线相交所构成的四个角中,邻补角有 对。对顶角有 对。
②形成的前提条件是两条直线相交。
4
2
性质:
1、邻补角的性质:邻补角 。
注意:邻补角是互补的一种特殊的情况,数量上 ,位置上有一条 。
互补
互补
公共边
性质:
如图,∵∠1+∠2 = ,∠2+∠3 = 。(邻补角定义)
∴∠1=180°- ,∠3 =180°- (等式性质)
∴∠1=∠3 (等量代换)
或者∵∠1与∠2互补,∠3与∠2互补(邻补角定义)
∴∠l=∠3(同角的补角相等).
由上面推理可知,
2、对顶角的性质:对顶角 。
B
A
C
D
O
1
2
3
4
180 °
180 °
∠2
∠2
相等
应用:
例 1. 如图,已知直线a、b相交。∠1=40°,求∠2、∠3、∠4的度数
解:
∵∠3=∠1=40°( )。
∴∠2=180°-∠1=180°-40°=140° ( )。
∴∠4=∠2=140°( )。
对顶角相等
邻补角定义
对顶角相等
收获:
1、两条直线相交所得的四个角中,有一个公共顶点,没有公共边的两个角叫做对顶角。不仅有一个公共顶点,还有一条公共边的两个角叫做邻补角。
2、数量关系是邻补角互补,对顶角相等。
3、用对顶角和邻补角的性质进行简单的推理和证明。
自我检测:
(一)选择题:
1、如图所示,∠1和∠2是对顶角的图形有( )
A.1个 B.2个 C.3个 D.4个
A
2、如图(1)所示,三条直线AB,CD,EF相交于一点O,则∠AOE+∠DOB+∠COF等于( )
A.150° B.180° C.210° D.120°
(1)
B
3、下列说法正确的有( )
①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等.
A.1个 B.2个 C.3个 D.4个
B
4、如图(2)所示,直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC的度数为( )
A.62° B.118° C.72° D.59°
(2)
A
(二)填空题:
1、如图(3)所示,AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角___.
2、如图(3)所示,若∠1=25°,则∠2=______,∠3=______,∠4=_____.
(3)
∠2或∠4
∠3
155 °
25 °
155 °
3、如图(4)所示,直线AB,CD相交于点O,若∠1-∠2=70 °,则∠BOD=_____,∠2=____.
(4)
125 °
55 °
六、拓展延伸:
1、如图所示,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.
b c
a
1
2
3
4
2、如图所示, 直线AB,CD相交于点O,OE平分∠AOD,∠AOC=120°,求∠BOD,∠AOE的 度数.
C
A
E O B
D
角的名称
邻补角
对顶角
位置关系
2、有一条公共边
3、另一边互为反向延长线
1、有公共顶点
1、有公共顶点
2、没有公共边
3、两边互为反向延长线
性质
邻补角互补
对顶角相等
相同点
都有一个公共顶点,它们都是成对出现的
不同点
对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个
知识回顾:
课本P121 习题1 , 2
作业
谢 谢
