2021-2022学年湖南师大附中梅溪湖中学九年级(下)开学数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年湖南师大附中梅溪湖中学九年级(下)开学数学试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 422.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 17:00:39 | ||
图片预览




文档简介
2021-2022学年湖南师大附中梅溪湖中学九年级(下)开学数学试卷
副标题
题号 一 二 三 四 总分
得分
一、选择题(本大题共10小题,共30.0分)
下列实数是无理数的是
A. B. C. D.
某个几何体的三视图如图所示,该几何体是
A.
B.
C.
D.
年月日,第七次全国人口普查结果发布,长沙市人口总数首次突破千万,约为人,将数据用科学记数法表示为
A. B. C. D.
下列运算中,正确的是
A. B.
C. D.
一个扇形的半径为,圆心角为,则该扇形的面积是
A. B. C. D.
若关于的一元二次方程有两个相等实数根,则的值是
A. B. C. D.
下列说法正确的是
A. 任意掷一枚质地均匀的硬币次,一定有次正面向上
B. 天气预报说“明天的降水概率为”,表示明天有的时间都在降雨
C. “篮球队员在罚球线上投篮一次,投中”为随机事件
D. “是实数,”是不可能事件
如图,菱形的对角线,的长分别为,,则这个菱形的周长为.
A.
B.
C.
D.
随着网络技术的发展,市场对产品的需求越来越大,为满足市场需求,某大型产品生产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产万件产品,现在生产万件产品所需时间与更新技术前生产万件产品所需时间相同.设更新技术前每天生产万件产品,依题意得
A. B. C. D.
已知抛物线与轴最多有一个交点,现有以下四个结论:
该抛物线的对称轴在轴右侧;关于的方程无实数根;;的最小值为其中正确结论的个数为
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共6小题,共18.0分)
式子在实数范围内有意义,则实数的取值范围是______.
分解因式:______.
在平面直角坐标系中,将点向右平移个单位长度,再向下平移个单位长度,那么平移后对应的点的坐标是______.
如图,为的直径,弦于点,已知,,则的半径为______.
如图,在中,,,,则的长是______ .
如图,点是函数与的图象在第一象限内的交点,,则的值为______.
三、计算题(本大题共1小题,共6.0分)
计算:.
四、解答题(本大题共8小题,共66.0分)
先化简,再求值:,其中.
人教版初中数学教科书八年级上册第页告诉我们一种作已知角的平分线的方法:
已知:.
求作:的平分线.
作法:以点为圆心,适当长为半径画弧,交于点,交于点.
分别以点,为圆心,大于的长为半径画弧,两弧在的内部相交于点.
画射线,射线即为所求如图.
请你根据提供的材料完成下面问题.
这种作已知角的平分线的方法的依据是______填序号
请你证明为的平分线.
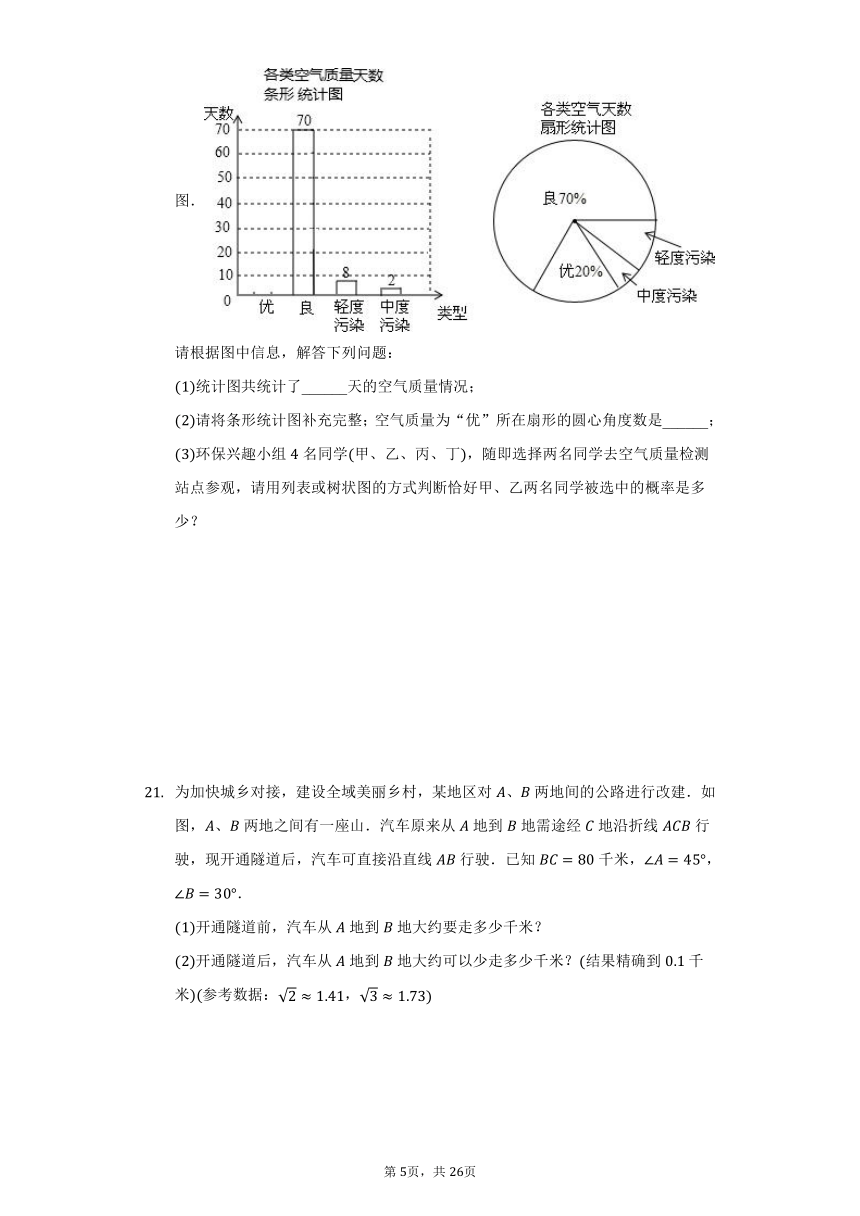
“美丽郑州”是我们的共同愿景,空气质量备受人们关注.我市某空气质量检测站点检测了该区域每天的空气质量情况,统计了年月份至月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.
请根据图中信息,解答下列问题:
统计图共统计了______天的空气质量情况;
请将条形统计图补充完整;空气质量为“优”所在扇形的圆心角度数是______;
环保兴趣小组名同学甲、乙、丙、丁,随即选择两名同学去空气质量检测站点参观,请用列表或树状图的方式判断恰好甲、乙两名同学被选中的概率是多少?
为加快城乡对接,建设全域美丽乡村,某地区对、两地间的公路进行改建.如图,、两地之间有一座山.汽车原来从地到地需途经地沿折线行驶,现开通隧道后,汽车可直接沿直线行驶.已知千米,,.
开通隧道前,汽车从地到地大约要走多少千米?
开通隧道后,汽车从地到地大约可以少走多少千米?结果精确到千米参考数据:,
年月日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知辆大型渣土运输车与辆小型渣土运输车一次共运输土方吨,辆大型渣土运输车与辆小型渣土运输车一次共运输土方吨.
一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
该渣土运输公司决定派出大、小两种型号的渣土运输车共辆参与运输土方,若每次运输土方总量不少于吨,且小型渣土运输车至少派出辆,则有哪几种派车方案?
如图,以的边上一点为圆心,经过、两点且与边交于点,点为的下半弧的中点,连接交线段于点,若.
求的度数;
求证:是的切线;
若,,求线段的长.
若一次函数与反比例函数同时经过点则称二次函数为一次函数与反比例函数的“共享函数”,称点为共享点.
判断与是否存在“共享函数”,如果存在,请求出“共享点”如果不存在,请说明理由;
已知:整数,,满足条件,并且一次函数与反比例函数存在“共享函数”,求的值.
若一次函数和反比例函数在自变量的值满足的的情况下.其“共享函数”的最小值为,求其“共享函数”的解析式.
如图,已知抛物线与轴交于、两点点在点左侧,与轴交于点,对称轴是直线,的外接圆交轴的正半轴与点,连结、,并延长交轴于点.
求抛物线的函数表达式和直线的函数表达式;
求证:∽;
如图,为轴正半轴上的一个动点,,,过点与轴平行的直线交抛物线与点,若的面积为,写出与的函数表达式,问:当为何值时,的面积最大,且最大面积为多少?
答案和解析
1.【答案】
【解析】
解:因为是整数,所以不是无理数,故A选项不符合题意;
B.因为是整数,所以不是无理数,故B选项不符合题意;
C.因为是分数,所以不是无理数,故C选项不符合题意;
D.因为是无限不循环小数,所以是无理数,故D选项符合题意.
故选:.
根据无理数的定义,无限不循环小数叫做无理数进行判定即可得出答案.
本题主要考查了无理数,熟练应用无理数的定义进行求解是解决本题的关键.
2.【答案】
【解析】
解:由三视图可知:该几何体为圆锥.
故选:.
根据几何体的三视图判断即可.
本题考查了由三视图判断几何体的知识,解题的关键是具有较强的空间想象能力,难度不大.
3.【答案】
【解析】
解:.
故选:.
用科学记数法表示较大的数时,一般形式为,其中,为整数,据此判断即可.
此题主要考查了用科学记数法表示较大的数,确定与的值是解题的关键.
4.【答案】
【解析】
【分析】
此题考查同类项、幂的乘方和完全平方公式,关键是根据法则进行计算.
根据同类项、幂的乘方和完全平方公式计算即可.
【解答】
解:、与不能合并,错误;
B、,正确;
C、,错误;
D、,错误;
故选B
5.【答案】
【解析】
【分析】
本题考查的是扇形面积的计算,掌握扇形的面积公式是解题的关键.
根据扇形的面积公式计算即可.
【解答】
解:扇形的面积是:.
6.【答案】
【解析】
【分析】
此题考查了根的判别式,熟练掌握根的判别式的意义是解本题的关键.
根据方程有两个相等的实数根,得到根的判别式的值等于,列出关于的方程,解方程可得的值.
【解答】
解:根据题意得:,即,
解得:,
故选:.
7.【答案】
【解析】
【分析】
此题主要考查了概率的意义以及随机事件的定义,正确把握相关定义是解题关键.
直接利用概率的意义以及随机事件的定义分别分析得出答案.
【解答】
解:、任意掷一枚质地均匀的硬币次,一定有次正面向上,错误;
B、天气预报说“明天的降水概率为”,表示明天有的时间都在降雨,错误;
C、“篮球队员在罚球线上投篮一次,投中”为随机事件,正确;
D、“是实数,”是必然事件,故此选项错误.
故选C.
8.【答案】
【解析】
【分析】
本题考查了菱形的性质,勾股定理,主要利用了菱形的对角线互相垂直平分,需熟记.
根据菱形的对角线互相垂直平分可得,,,再利用勾股定理列式求出,然后根据菱形的四条边都相等列式计算即可得解.
【解答】
解:四边形是菱形,
,,
,
根据勾股定理得,,
所以,这个菱形的周长.
故选D.
9.【答案】
【解析】
解:设更新技术前每天生产万件产品,则更新技术后每天生产万件产品,
依题意,得:.
故选:.
设更新技术前每天生产万件产品,则更新技术后每天生产万件产品,根据工作时间工作总量工作效率结合现在生产万件产品所需时间与更新技术前生产万件产品所需时间相同,即可得出关于的分式方程,此题得解.
本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
10.【答案】
【解析】
解:,
抛物线的对称轴,
错误.
已知抛物线与轴最多有一个交点,
,
,
关于的方程无实数根,
正确.
抛物线与轴最多有一个交点,
取任何数时,,
当时,,
,
.
正确.
抛物线与轴最多有一个交点,
当取任何数时,,
当时,,
,
,
.
正确.
故选:.
根据二次函数的图象和性质判断即可.
本题考查二次函数的图象和性质,掌握二次函数的图象和性质是求解本题的关键.
11.【答案】
【解析】
【分析】
此题主要考查了二次根式有意义的条件,正确把握相关定义是解题关键.直接利用二次根式有意义的条件进而得出答案.
【解答】
解:式子在实数范围内有意义,则,
故实数的取值范围是:.
故答案为.
12.【答案】
【解析】
解:,
,
.
故答案为:.
先提取公因式,然后再利用平方差公式进行二次分解.
本题考查了提公因式法,公式法分解因式,利用平方差公式进行二次分解因式是解本题的难点,也是关键.
13.【答案】
【解析】
解:将点向右平移个单位长度,
得到,
再向下平移个单位长度,
平移后对应的点的坐标是:.
故答案为:.
直接利用平移的性质分别得出平移后点的坐标得出答案.
此题主要考查了平移,正确掌握平移规律是解题关键.
14.【答案】
【解析】
【分析】
本题利用了垂径定理和勾股定理求解,熟练掌握并应用定理是解题的关键.
连接,由垂径定理知,点是的中点,,在直角中,利用勾股定理即可得到关于半径的方程,求得圆半径即可.
【解答】
解:连接,
为的直径,,
,
设的半径为,
则,,
在中,,
,
解得:,
的半径为,
故答案为:.
15.【答案】
【解析】
解:,
::,
即::,
.
故答案为:.
由平行可得到::,由可求得.
本题主要考查平行线分线段成比例定理,掌握平行线分线段所得线段对应成比例是解题的关键.
16.【答案】
【解析】
【分析】
本题考查了反比例函数与一次函数的图象得交点、勾股定理、反比例函数解析式的求法;求出点的坐标是解决问题的关键.
作轴于,得出,在中,由勾股定理得出方程,解方程求出,得出,即可求出的值.
【解答】
解:作轴于,如图所示:
设,
点是函数与的图象在第一象限内的交点,
,
在中,由勾股定理得:,
解得:,
,
代入得:;
故答案为.
17.【答案】
解:原式
.
【解析】
首先化简绝对值,求零指数幂,特殊角的三角函数,负整数指数幂,再按顺序进行加减运算.
本题主要考查了化简绝对值,零指数幂,特殊角的三角函数,负整数指数幂,熟练掌握实数的运算法则是解答此题的关键.
18.【答案】
解:原式
,
当时,
原式
.
【解析】
直接利用乘法公式结合整式的混合运算法则化简,再把已知数据代入得出答案.
此题主要考查了整式的混合运算化简求值,正确运用乘法公式是解题关键.
19.【答案】
解:;
由基本作图方法可得:,,,
则在和中,
,
≌,
,
即为的平分线.
【解析】
【分析】
此题主要考查了应用设计与作图,正确掌握全等三角形的判定方法是解题关键.
直接利用角平分线的作法得出基本依据;
直接利用全等三角形的判定与性质得出答案.
【解答】
解:这种作已知角的平分线的方法的依据是.
故答案为:;
见答案.
20.【答案】
;
画树状图得:
所有出现的等可能性结果共有种,其中满足条件的结果有种.
恰好选中甲、乙两名同学的概率为..
【解析】
解:良有天,占,
统计图统计的空气质量情况的天数为:天,
故答案为:;
如图:条形统计图中,空气质量为“优”的天数为天,
空气质量为“优”所在扇形的圆心角度数是:,
补全图形如下:
故答案为:;
见答案
由良有天,占,即可求得统计图共统计了几天的空气质量情况;
由条形统计图中,可得空气质量为“良”的天数为天,空气质量为“优”所在扇形的圆心角度数是:,
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好甲、乙两名同学被选中的情况,再利用概率公式即可求得答案.
本题考查的是用列表法或画树状图法求概率以及扇形统计图与条形统计图的知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
21.【答案】
解:如图,过点作的垂线,垂足为,
,,千米,
千米,千米,
千米.
开通隧道前,汽车从地到地大约要走千米.
,千米,
千米,
,千米,
千米,
千米.
汽车从地到地比原来少走的路程为:
千米.
开通隧道后,汽车从地到地大约可以少走千米.
【解析】
开通隧道前,汽车从地到地要走的距离为的长,利用角的正弦值和余弦值即可算出.
开通隧道后,汽车从地到地要走的距离为的长,汽车从地到地比原来少走的路程为的长,利用角的余弦值和正切值即可算出.
本题主要考查了三角函数在解直角三角形中的应用,明确三角函数的定义式及其变形是解题的关键.
22.【答案】
解:设一辆大型渣土运输车一次运输吨,一辆小型渣土运输车一次运输吨,
,
解得.
即一辆大型渣土运输车一次运输吨,一辆小型渣土运输车一次运输吨;
由题意可得,
设该渣土运输公司决定派出大、小两种型号的渣土运输车分别为辆、辆,
解得或或,
故有三种派车方案,
第一种方案:大型运输车辆,小型运输车辆;
第二种方案:大型运输车辆,小型运输车辆;
第三种方案:大型运输车辆,小型运输车辆.
【解析】
根据题意可以得到相应的二元一次方程,从而可以求得一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨;
根据题意可以列出相应的关系式,从而可以求得有几种方案.
本题考查一元一次不等式组的应用、二元一次方程组的应用,解题的关键是明确题意,找出所求问题需要的条件.
23.【答案】
解:为直径,为的中点,
的度数是,
;
证明:连接,
,
,
为半径,为的中点,
,
,
,
,,
,
即,
是的切线;
解:设,
在中,,
,,
,
解得:或,
,
舍去,
即,,,
是的切线,是的割线,
由切割线定理得:,
,
,
解得:.
【解析】
求出的度数是,根据圆周角定理得出即可;
求出,根据切线的判定得出即可;
根据勾股定理求出半径,根据切割线定理得出,代入即可求出.
本题考查了垂径定理,切割线定理,圆周角定理,等腰三角形的性质和判定等知识点,能综合运用定理进行推理是解此题的关键.
24.【答案】
解:联立与并整理得:
,解得:或,
故点的坐标为:或;
由题意得:,解得:,
,
,
解得:;
,
故,
是整数,故;
由和反比例函数得:“共享函数”的解析式为,
函数的对称轴为:;
当时,即,
,函数取得最小值,即,
解得舍去;
当,即,
函数在处取得最小值,即,无解;
当时,
函数在处,取得最小值,即,解得:舍去,
综上,,
故“共享函数”的解析式为.
【解析】
联立与并整理得:,即可求解;
由题意得:,解得:,而,故,则,故,是整数,故;
当时,即,,函数取得最小值,即,即可求解;当,即,函数在处取得最小值,即,即可求解;当时,函数在处,取得最小值,即可求解.
本题考查的是二次函数综合运用,涉及到一次函数和反比例函数,这种新定义类的题目,通常按照题设的顺序逐次求解,其中,要注意分类求解,避免出错.
25.【答案】
解:解:抛物线的对称轴为直线,
,
,
抛物线与轴交于点,
,
抛物线的函数表达式为:;
,,
设直线的解析式为,
,解得
直线的解析式为;
连,
,,
,,
,
,
,
,
∽;
,
∽,
,
,,
,
,
,
,
当时,的面积最大,最大面积是.
【解析】
本题主要考查了二次函数的综合题型以及相似三角形的判定和性质、圆周角定理、待定系数法求一次函数解析式等知识,将函数坐标问题进行转化是解题的关键.
利用对称轴公式即可得出的值,再利用抛物线与轴交于点,求出抛物线解析式即可;
连,由圆周角定理可得,可证,则∽;
先证明∽,由相似三角形性质可用表示、的长,再根据可求得面积的最大值.
第2页,共2页
第1页,共1页
副标题
题号 一 二 三 四 总分
得分
一、选择题(本大题共10小题,共30.0分)
下列实数是无理数的是
A. B. C. D.
某个几何体的三视图如图所示,该几何体是
A.
B.
C.
D.
年月日,第七次全国人口普查结果发布,长沙市人口总数首次突破千万,约为人,将数据用科学记数法表示为
A. B. C. D.
下列运算中,正确的是
A. B.
C. D.
一个扇形的半径为,圆心角为,则该扇形的面积是
A. B. C. D.
若关于的一元二次方程有两个相等实数根,则的值是
A. B. C. D.
下列说法正确的是
A. 任意掷一枚质地均匀的硬币次,一定有次正面向上
B. 天气预报说“明天的降水概率为”,表示明天有的时间都在降雨
C. “篮球队员在罚球线上投篮一次,投中”为随机事件
D. “是实数,”是不可能事件
如图,菱形的对角线,的长分别为,,则这个菱形的周长为.
A.
B.
C.
D.
随着网络技术的发展,市场对产品的需求越来越大,为满足市场需求,某大型产品生产厂家更新技术后,加快了生产速度,现在平均每天比更新技术前多生产万件产品,现在生产万件产品所需时间与更新技术前生产万件产品所需时间相同.设更新技术前每天生产万件产品,依题意得
A. B. C. D.
已知抛物线与轴最多有一个交点,现有以下四个结论:
该抛物线的对称轴在轴右侧;关于的方程无实数根;;的最小值为其中正确结论的个数为
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共6小题,共18.0分)
式子在实数范围内有意义,则实数的取值范围是______.
分解因式:______.
在平面直角坐标系中,将点向右平移个单位长度,再向下平移个单位长度,那么平移后对应的点的坐标是______.
如图,为的直径,弦于点,已知,,则的半径为______.
如图,在中,,,,则的长是______ .
如图,点是函数与的图象在第一象限内的交点,,则的值为______.
三、计算题(本大题共1小题,共6.0分)
计算:.
四、解答题(本大题共8小题,共66.0分)
先化简,再求值:,其中.
人教版初中数学教科书八年级上册第页告诉我们一种作已知角的平分线的方法:
已知:.
求作:的平分线.
作法:以点为圆心,适当长为半径画弧,交于点,交于点.
分别以点,为圆心,大于的长为半径画弧,两弧在的内部相交于点.
画射线,射线即为所求如图.
请你根据提供的材料完成下面问题.
这种作已知角的平分线的方法的依据是______填序号
请你证明为的平分线.
“美丽郑州”是我们的共同愿景,空气质量备受人们关注.我市某空气质量检测站点检测了该区域每天的空气质量情况,统计了年月份至月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图.
请根据图中信息,解答下列问题:
统计图共统计了______天的空气质量情况;
请将条形统计图补充完整;空气质量为“优”所在扇形的圆心角度数是______;
环保兴趣小组名同学甲、乙、丙、丁,随即选择两名同学去空气质量检测站点参观,请用列表或树状图的方式判断恰好甲、乙两名同学被选中的概率是多少?
为加快城乡对接,建设全域美丽乡村,某地区对、两地间的公路进行改建.如图,、两地之间有一座山.汽车原来从地到地需途经地沿折线行驶,现开通隧道后,汽车可直接沿直线行驶.已知千米,,.
开通隧道前,汽车从地到地大约要走多少千米?
开通隧道后,汽车从地到地大约可以少走多少千米?结果精确到千米参考数据:,
年月日,中国第一条具有自主知识产权的长沙磁浮线正式开通运营,该路线连接了长沙火车南站和黄花国际机场两大交通枢纽,沿线生态绿化带走廊的建设尚在进行中,届时将给乘客带来美的享受.星城渣土运输公司承包了某标段的土方运输任务,拟派出大、小两种型号的渣土运输车运输土方,已知辆大型渣土运输车与辆小型渣土运输车一次共运输土方吨,辆大型渣土运输车与辆小型渣土运输车一次共运输土方吨.
一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨?
该渣土运输公司决定派出大、小两种型号的渣土运输车共辆参与运输土方,若每次运输土方总量不少于吨,且小型渣土运输车至少派出辆,则有哪几种派车方案?
如图,以的边上一点为圆心,经过、两点且与边交于点,点为的下半弧的中点,连接交线段于点,若.
求的度数;
求证:是的切线;
若,,求线段的长.
若一次函数与反比例函数同时经过点则称二次函数为一次函数与反比例函数的“共享函数”,称点为共享点.
判断与是否存在“共享函数”,如果存在,请求出“共享点”如果不存在,请说明理由;
已知:整数,,满足条件,并且一次函数与反比例函数存在“共享函数”,求的值.
若一次函数和反比例函数在自变量的值满足的的情况下.其“共享函数”的最小值为,求其“共享函数”的解析式.
如图,已知抛物线与轴交于、两点点在点左侧,与轴交于点,对称轴是直线,的外接圆交轴的正半轴与点,连结、,并延长交轴于点.
求抛物线的函数表达式和直线的函数表达式;
求证:∽;
如图,为轴正半轴上的一个动点,,,过点与轴平行的直线交抛物线与点,若的面积为,写出与的函数表达式,问:当为何值时,的面积最大,且最大面积为多少?
答案和解析
1.【答案】
【解析】
解:因为是整数,所以不是无理数,故A选项不符合题意;
B.因为是整数,所以不是无理数,故B选项不符合题意;
C.因为是分数,所以不是无理数,故C选项不符合题意;
D.因为是无限不循环小数,所以是无理数,故D选项符合题意.
故选:.
根据无理数的定义,无限不循环小数叫做无理数进行判定即可得出答案.
本题主要考查了无理数,熟练应用无理数的定义进行求解是解决本题的关键.
2.【答案】
【解析】
解:由三视图可知:该几何体为圆锥.
故选:.
根据几何体的三视图判断即可.
本题考查了由三视图判断几何体的知识,解题的关键是具有较强的空间想象能力,难度不大.
3.【答案】
【解析】
解:.
故选:.
用科学记数法表示较大的数时,一般形式为,其中,为整数,据此判断即可.
此题主要考查了用科学记数法表示较大的数,确定与的值是解题的关键.
4.【答案】
【解析】
【分析】
此题考查同类项、幂的乘方和完全平方公式,关键是根据法则进行计算.
根据同类项、幂的乘方和完全平方公式计算即可.
【解答】
解:、与不能合并,错误;
B、,正确;
C、,错误;
D、,错误;
故选B
5.【答案】
【解析】
【分析】
本题考查的是扇形面积的计算,掌握扇形的面积公式是解题的关键.
根据扇形的面积公式计算即可.
【解答】
解:扇形的面积是:.
6.【答案】
【解析】
【分析】
此题考查了根的判别式,熟练掌握根的判别式的意义是解本题的关键.
根据方程有两个相等的实数根,得到根的判别式的值等于,列出关于的方程,解方程可得的值.
【解答】
解:根据题意得:,即,
解得:,
故选:.
7.【答案】
【解析】
【分析】
此题主要考查了概率的意义以及随机事件的定义,正确把握相关定义是解题关键.
直接利用概率的意义以及随机事件的定义分别分析得出答案.
【解答】
解:、任意掷一枚质地均匀的硬币次,一定有次正面向上,错误;
B、天气预报说“明天的降水概率为”,表示明天有的时间都在降雨,错误;
C、“篮球队员在罚球线上投篮一次,投中”为随机事件,正确;
D、“是实数,”是必然事件,故此选项错误.
故选C.
8.【答案】
【解析】
【分析】
本题考查了菱形的性质,勾股定理,主要利用了菱形的对角线互相垂直平分,需熟记.
根据菱形的对角线互相垂直平分可得,,,再利用勾股定理列式求出,然后根据菱形的四条边都相等列式计算即可得解.
【解答】
解:四边形是菱形,
,,
,
根据勾股定理得,,
所以,这个菱形的周长.
故选D.
9.【答案】
【解析】
解:设更新技术前每天生产万件产品,则更新技术后每天生产万件产品,
依题意,得:.
故选:.
设更新技术前每天生产万件产品,则更新技术后每天生产万件产品,根据工作时间工作总量工作效率结合现在生产万件产品所需时间与更新技术前生产万件产品所需时间相同,即可得出关于的分式方程,此题得解.
本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.
10.【答案】
【解析】
解:,
抛物线的对称轴,
错误.
已知抛物线与轴最多有一个交点,
,
,
关于的方程无实数根,
正确.
抛物线与轴最多有一个交点,
取任何数时,,
当时,,
,
.
正确.
抛物线与轴最多有一个交点,
当取任何数时,,
当时,,
,
,
.
正确.
故选:.
根据二次函数的图象和性质判断即可.
本题考查二次函数的图象和性质,掌握二次函数的图象和性质是求解本题的关键.
11.【答案】
【解析】
【分析】
此题主要考查了二次根式有意义的条件,正确把握相关定义是解题关键.直接利用二次根式有意义的条件进而得出答案.
【解答】
解:式子在实数范围内有意义,则,
故实数的取值范围是:.
故答案为.
12.【答案】
【解析】
解:,
,
.
故答案为:.
先提取公因式,然后再利用平方差公式进行二次分解.
本题考查了提公因式法,公式法分解因式,利用平方差公式进行二次分解因式是解本题的难点,也是关键.
13.【答案】
【解析】
解:将点向右平移个单位长度,
得到,
再向下平移个单位长度,
平移后对应的点的坐标是:.
故答案为:.
直接利用平移的性质分别得出平移后点的坐标得出答案.
此题主要考查了平移,正确掌握平移规律是解题关键.
14.【答案】
【解析】
【分析】
本题利用了垂径定理和勾股定理求解,熟练掌握并应用定理是解题的关键.
连接,由垂径定理知,点是的中点,,在直角中,利用勾股定理即可得到关于半径的方程,求得圆半径即可.
【解答】
解:连接,
为的直径,,
,
设的半径为,
则,,
在中,,
,
解得:,
的半径为,
故答案为:.
15.【答案】
【解析】
解:,
::,
即::,
.
故答案为:.
由平行可得到::,由可求得.
本题主要考查平行线分线段成比例定理,掌握平行线分线段所得线段对应成比例是解题的关键.
16.【答案】
【解析】
【分析】
本题考查了反比例函数与一次函数的图象得交点、勾股定理、反比例函数解析式的求法;求出点的坐标是解决问题的关键.
作轴于,得出,在中,由勾股定理得出方程,解方程求出,得出,即可求出的值.
【解答】
解:作轴于,如图所示:
设,
点是函数与的图象在第一象限内的交点,
,
在中,由勾股定理得:,
解得:,
,
代入得:;
故答案为.
17.【答案】
解:原式
.
【解析】
首先化简绝对值,求零指数幂,特殊角的三角函数,负整数指数幂,再按顺序进行加减运算.
本题主要考查了化简绝对值,零指数幂,特殊角的三角函数,负整数指数幂,熟练掌握实数的运算法则是解答此题的关键.
18.【答案】
解:原式
,
当时,
原式
.
【解析】
直接利用乘法公式结合整式的混合运算法则化简,再把已知数据代入得出答案.
此题主要考查了整式的混合运算化简求值,正确运用乘法公式是解题关键.
19.【答案】
解:;
由基本作图方法可得:,,,
则在和中,
,
≌,
,
即为的平分线.
【解析】
【分析】
此题主要考查了应用设计与作图,正确掌握全等三角形的判定方法是解题关键.
直接利用角平分线的作法得出基本依据;
直接利用全等三角形的判定与性质得出答案.
【解答】
解:这种作已知角的平分线的方法的依据是.
故答案为:;
见答案.
20.【答案】
;
画树状图得:
所有出现的等可能性结果共有种,其中满足条件的结果有种.
恰好选中甲、乙两名同学的概率为..
【解析】
解:良有天,占,
统计图统计的空气质量情况的天数为:天,
故答案为:;
如图:条形统计图中,空气质量为“优”的天数为天,
空气质量为“优”所在扇形的圆心角度数是:,
补全图形如下:
故答案为:;
见答案
由良有天,占,即可求得统计图共统计了几天的空气质量情况;
由条形统计图中,可得空气质量为“良”的天数为天,空气质量为“优”所在扇形的圆心角度数是:,
首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好甲、乙两名同学被选中的情况,再利用概率公式即可求得答案.
本题考查的是用列表法或画树状图法求概率以及扇形统计图与条形统计图的知识.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率所求情况数与总情况数之比.
21.【答案】
解:如图,过点作的垂线,垂足为,
,,千米,
千米,千米,
千米.
开通隧道前,汽车从地到地大约要走千米.
,千米,
千米,
,千米,
千米,
千米.
汽车从地到地比原来少走的路程为:
千米.
开通隧道后,汽车从地到地大约可以少走千米.
【解析】
开通隧道前,汽车从地到地要走的距离为的长,利用角的正弦值和余弦值即可算出.
开通隧道后,汽车从地到地要走的距离为的长,汽车从地到地比原来少走的路程为的长,利用角的余弦值和正切值即可算出.
本题主要考查了三角函数在解直角三角形中的应用,明确三角函数的定义式及其变形是解题的关键.
22.【答案】
解:设一辆大型渣土运输车一次运输吨,一辆小型渣土运输车一次运输吨,
,
解得.
即一辆大型渣土运输车一次运输吨,一辆小型渣土运输车一次运输吨;
由题意可得,
设该渣土运输公司决定派出大、小两种型号的渣土运输车分别为辆、辆,
解得或或,
故有三种派车方案,
第一种方案:大型运输车辆,小型运输车辆;
第二种方案:大型运输车辆,小型运输车辆;
第三种方案:大型运输车辆,小型运输车辆.
【解析】
根据题意可以得到相应的二元一次方程,从而可以求得一辆大型渣土运输车和一辆小型渣土运输车一次各运输土方多少吨;
根据题意可以列出相应的关系式,从而可以求得有几种方案.
本题考查一元一次不等式组的应用、二元一次方程组的应用,解题的关键是明确题意,找出所求问题需要的条件.
23.【答案】
解:为直径,为的中点,
的度数是,
;
证明:连接,
,
,
为半径,为的中点,
,
,
,
,,
,
即,
是的切线;
解:设,
在中,,
,,
,
解得:或,
,
舍去,
即,,,
是的切线,是的割线,
由切割线定理得:,
,
,
解得:.
【解析】
求出的度数是,根据圆周角定理得出即可;
求出,根据切线的判定得出即可;
根据勾股定理求出半径,根据切割线定理得出,代入即可求出.
本题考查了垂径定理,切割线定理,圆周角定理,等腰三角形的性质和判定等知识点,能综合运用定理进行推理是解此题的关键.
24.【答案】
解:联立与并整理得:
,解得:或,
故点的坐标为:或;
由题意得:,解得:,
,
,
解得:;
,
故,
是整数,故;
由和反比例函数得:“共享函数”的解析式为,
函数的对称轴为:;
当时,即,
,函数取得最小值,即,
解得舍去;
当,即,
函数在处取得最小值,即,无解;
当时,
函数在处,取得最小值,即,解得:舍去,
综上,,
故“共享函数”的解析式为.
【解析】
联立与并整理得:,即可求解;
由题意得:,解得:,而,故,则,故,是整数,故;
当时,即,,函数取得最小值,即,即可求解;当,即,函数在处取得最小值,即,即可求解;当时,函数在处,取得最小值,即可求解.
本题考查的是二次函数综合运用,涉及到一次函数和反比例函数,这种新定义类的题目,通常按照题设的顺序逐次求解,其中,要注意分类求解,避免出错.
25.【答案】
解:解:抛物线的对称轴为直线,
,
,
抛物线与轴交于点,
,
抛物线的函数表达式为:;
,,
设直线的解析式为,
,解得
直线的解析式为;
连,
,,
,,
,
,
,
,
∽;
,
∽,
,
,,
,
,
,
,
当时,的面积最大,最大面积是.
【解析】
本题主要考查了二次函数的综合题型以及相似三角形的判定和性质、圆周角定理、待定系数法求一次函数解析式等知识,将函数坐标问题进行转化是解题的关键.
利用对称轴公式即可得出的值,再利用抛物线与轴交于点,求出抛物线解析式即可;
连,由圆周角定理可得,可证,则∽;
先证明∽,由相似三角形性质可用表示、的长,再根据可求得面积的最大值.
第2页,共2页
第1页,共1页
同课章节目录
