6.2导数的应用 讲义+练习-2021-2022学年高中数学人教B版(2019)选择性必修第三册(含答案)
文档属性
| 名称 | 6.2导数的应用 讲义+练习-2021-2022学年高中数学人教B版(2019)选择性必修第三册(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 865.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 15:38:50 | ||
图片预览


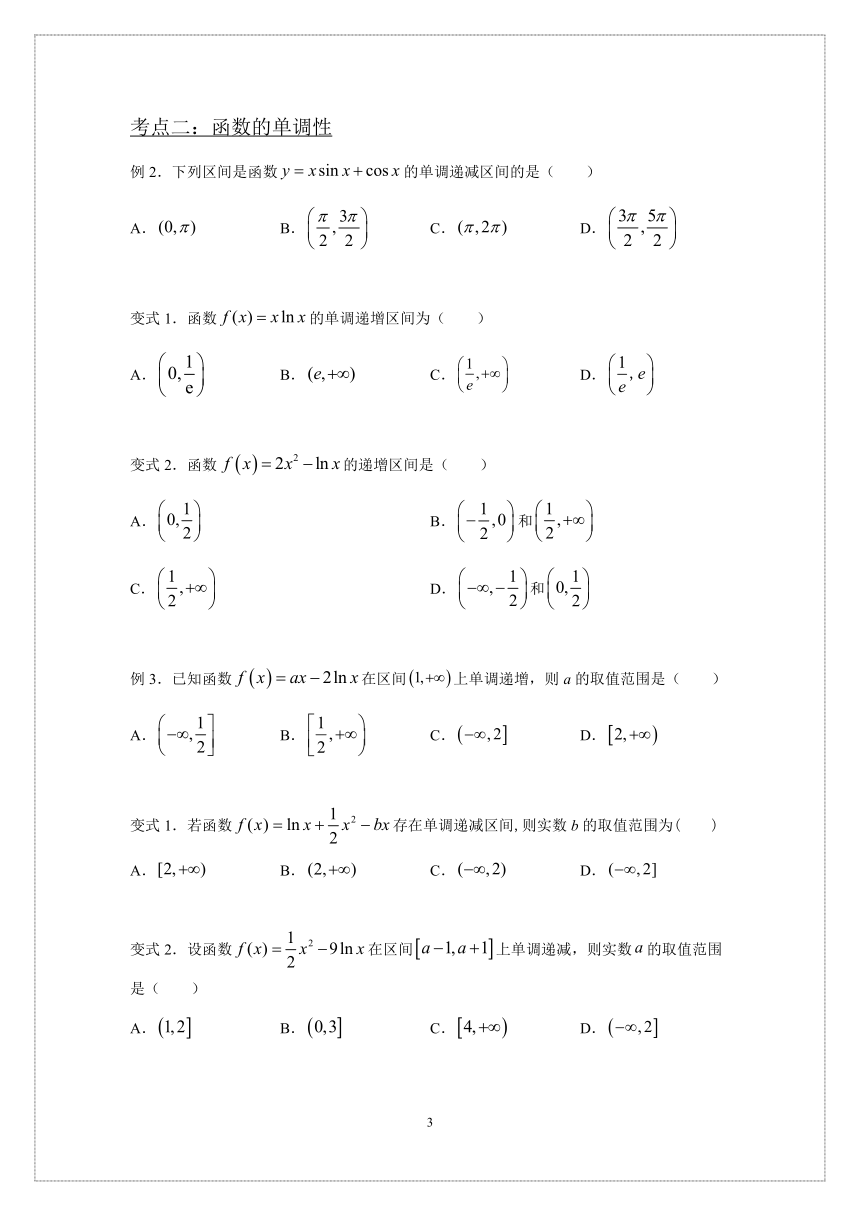
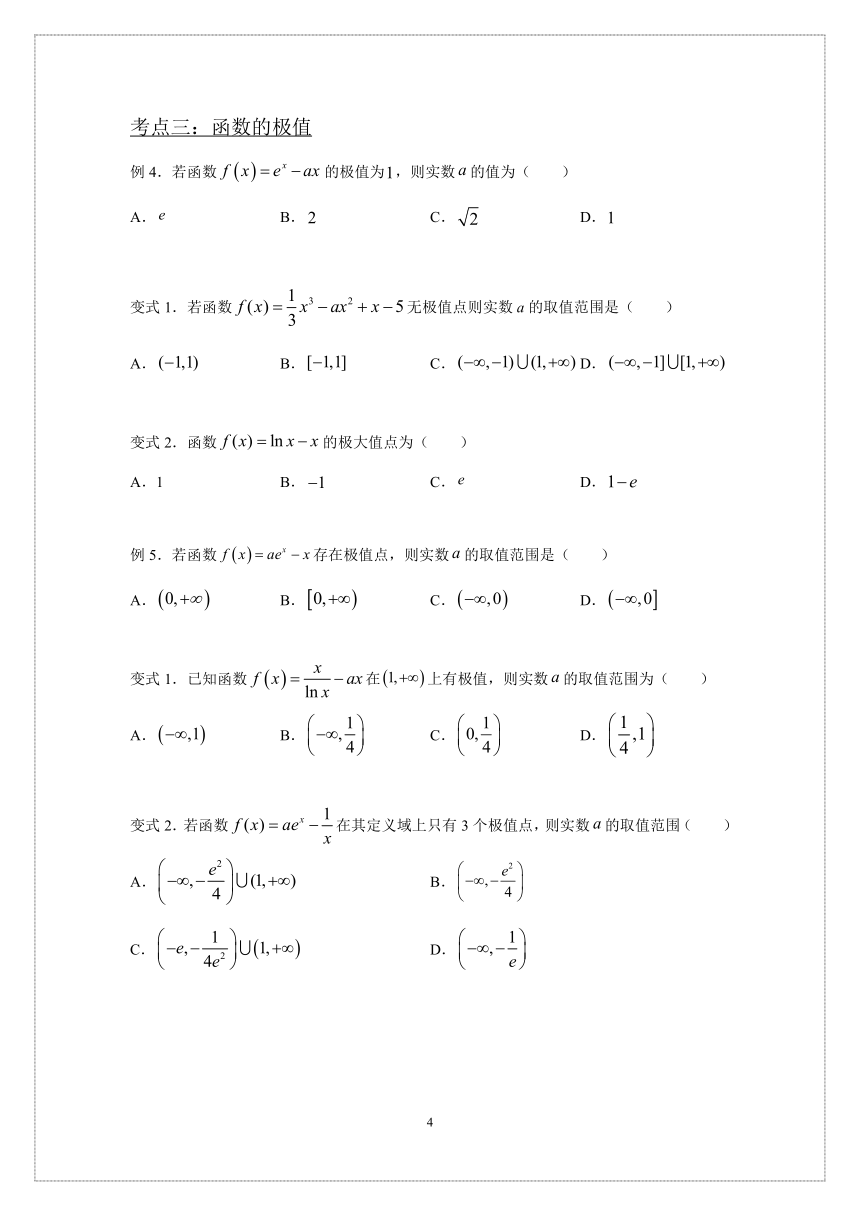

文档简介
6.2 导数的应用(新课)
知识梳理
1.利用导数判断函数的单调性的方法:
如果函数在的某个开区间内,总有,则在这个区间上是增函数;如果函数在的某个开区间内,总有,则在这个区间上是减函数.
2.利用导数研究函数的极值:
已知函数,设是定义域内任一点,如果对附近的所有点,都有,则称函数在点处取极大值,记作.并把称为函数的一个极大值点.
如果在附近都有,则称函数在点处取极小值,记作.并把称为函数的一个极小值点.
极大值与极小值统称为极值.极大值点与极小值点统称为极值点.
3.求函数的极值的方法:
第1步 求导数;
第2步 求方程的所有实数根;
第步 考察在每个根附近,从左到右,导函数的符号如何变化.如果的符号由正变负,则是极大值;如果由负变正,则是极小值.如果在的根的左右侧,的符号不变,则不是极值.
4.函数的最大(小)值是函数在指定区间的最大(小)的值.
求函数最大(小)值的方法:
第1步 求在指定区间内所有使的点;
第2步 计算函数在区间内使的所有点和区间端点的函数值,其中最大的为最大值,最小的为最小值.
典例讲解
考点一:原函数与导函数的图象
例1.设函数在定义域内可导,的图象如图所示,则导函数的图象为( )
A. B.C.D.
变式1.已知函数的图象如图所示,则的图象可能是( )
A. B. C. D.
变式2.已知函数的导函数的图象如图所示,那么函数的图象最有可能的是( )
A. B.C. D.
考点二:函数的单调性
例2.下列区间是函数的单调递减区间的是( )
A. B. C. D.
变式1.函数的单调递增区间为( )
A. B. C. D.
变式2.函数的递增区间是( )
A. B.和
C. D.和
例3.已知函数在区间上单调递增,则a的取值范围是( )
A. B. C. D.
变式1.若函数存在单调递减区间,则实数b的取值范围为( )
A. B. C. D.
变式2.设函数在区间上单调递减,则实数的取值范围是( )
A. B. C. D.
考点三:函数的极值
例4.若函数的极值为,则实数的值为( )
A. B. C. D.
变式1.若函数无极值点则实数a的取值范围是( )
A. B. C. D.
变式2.函数的极大值点为( )
A.1 B. C. D.
例5.若函数存在极值点,则实数的取值范围是( )
A. B. C. D.
变式1.已知函数在上有极值,则实数的取值范围为( )
A. B. C. D.
变式2.若函数在其定义域上只有3个极值点,则实数的取值范围( )
A. B.
C. D.
考点四:函数的最值
例6.函数在区间上的最小值是( )
A. B. C.11 D.
变式1.若函数在区间上的最大值为M,最小值为N,则( )
A.14 B.12 C.10 D.8
变式2.若,则的最大值为( )
A. B. C.3 D.2
例7.已知函数存在最大值0,则a的值为( )
A.1 B.2 C.e D.
变式1.若函数在区间上有最小值,则实数取值范围是( )
A. B. C. D.
变式2.函数在上的最大值为2,则a的值为( )
A. B.2 C.5 D.
考点五:导数的构造法
例8.已知f(x)是定义在R上的偶函数,且,当时,,则不等式的解集为( )
A.(-∞,2)∪(2,+∞) B.(-∞,2)∪(0,2) C.(-2,0)∪(2,+∞) D.(-2,0)∪(0,2)
变式1.已知为偶函数,且,令,若时,,关于的不等式的解集为( )
A.或 B.
C. D.或
变式2.已知为定义在上的偶函数,其导函数为,对于任意的总有成立,则下列不等式成立的有( )
A.B.C.D.
例9.已知是可导的函数,且,则下列不等关系正确的是( )
A., B.,
C., D.,
变式1.设定义在上的函数的导函数为,若,,则不等式(其中为自然对数的底数)的解集为( )
A. B. C. D.
变式2.已知函数的定义域为,为的导函数.若,且,则不等式的解集为( )
A. B. C. D.
巩固练习
1.已知函数的导函数的图象如右图所示,那么函数的图象最有可能的是( )
2.函数的单调递减区间为( )
A. B. C. D.
3.函数的单调递减区间是( )
A. B. C. D.
4.已知函数的单调递减区间为,则的值为( )
A. B. C. D.
5.若函数在区间上单调递减,则实数的取值范围为( )
A. B. C. D.
6.若函数在是增函数,则实数a的取值范围是( )
A. B. C. D.
7.设函数,则的极大值点和极小值点分别为( )
A.-2,2 B.2,-2 C.5,-3 D.-5,3
8.已知函数,则在上的最小值为( )
A. B. C. D.
9.设,若函数有大于零的极值点,则的取值范围为( )
A. B. C. D.
10.已知函数在处取极大值,则( )
A.-2或-6 B.2或6 C.6 D.2
11.若函数 在上有最大值3,则该函数在上最小值( )
A. B.0 C. D.1
12.函数的极值点的个数是( )
A.0 B.1 C.2 D.3
13.已知时,函数取得极大值,则( )
A. B. C.4 D.2
14.上的函数满足:,,则不等式的解集为( )
A. B.
C. D.
15.已知定义在上的奇函数满足(),则( )
A. B.
C. D.
16.定义在上的函数的导函数为,若,则不等式的解集是( )
A. B. C. D.
6.2导数的应用答案
典例讲解
例1.C
变式1.B
变式2.A
例2.B
变式1.C
变式2.C
例3.D
变式1.B
变式2.A
例4.D
变式1.B
变式2.A
例5.A
变式1.B
变式2.B
例6.A
变式1.B
变式2.A
例7.D
变式1.C
变式2.B
例8.B
变式1.C
变式2.C
例9.C
变式1.C
变式2.A
巩固练习
1. A
2.D
3.B
4.B
5.B
6.C
7.A
8.D
9.A
10.C
11.C
12.C
13.B
14.D
15.B
16.D
11
知识梳理
1.利用导数判断函数的单调性的方法:
如果函数在的某个开区间内,总有,则在这个区间上是增函数;如果函数在的某个开区间内,总有,则在这个区间上是减函数.
2.利用导数研究函数的极值:
已知函数,设是定义域内任一点,如果对附近的所有点,都有,则称函数在点处取极大值,记作.并把称为函数的一个极大值点.
如果在附近都有,则称函数在点处取极小值,记作.并把称为函数的一个极小值点.
极大值与极小值统称为极值.极大值点与极小值点统称为极值点.
3.求函数的极值的方法:
第1步 求导数;
第2步 求方程的所有实数根;
第步 考察在每个根附近,从左到右,导函数的符号如何变化.如果的符号由正变负,则是极大值;如果由负变正,则是极小值.如果在的根的左右侧,的符号不变,则不是极值.
4.函数的最大(小)值是函数在指定区间的最大(小)的值.
求函数最大(小)值的方法:
第1步 求在指定区间内所有使的点;
第2步 计算函数在区间内使的所有点和区间端点的函数值,其中最大的为最大值,最小的为最小值.
典例讲解
考点一:原函数与导函数的图象
例1.设函数在定义域内可导,的图象如图所示,则导函数的图象为( )
A. B.C.D.
变式1.已知函数的图象如图所示,则的图象可能是( )
A. B. C. D.
变式2.已知函数的导函数的图象如图所示,那么函数的图象最有可能的是( )
A. B.C. D.
考点二:函数的单调性
例2.下列区间是函数的单调递减区间的是( )
A. B. C. D.
变式1.函数的单调递增区间为( )
A. B. C. D.
变式2.函数的递增区间是( )
A. B.和
C. D.和
例3.已知函数在区间上单调递增,则a的取值范围是( )
A. B. C. D.
变式1.若函数存在单调递减区间,则实数b的取值范围为( )
A. B. C. D.
变式2.设函数在区间上单调递减,则实数的取值范围是( )
A. B. C. D.
考点三:函数的极值
例4.若函数的极值为,则实数的值为( )
A. B. C. D.
变式1.若函数无极值点则实数a的取值范围是( )
A. B. C. D.
变式2.函数的极大值点为( )
A.1 B. C. D.
例5.若函数存在极值点,则实数的取值范围是( )
A. B. C. D.
变式1.已知函数在上有极值,则实数的取值范围为( )
A. B. C. D.
变式2.若函数在其定义域上只有3个极值点,则实数的取值范围( )
A. B.
C. D.
考点四:函数的最值
例6.函数在区间上的最小值是( )
A. B. C.11 D.
变式1.若函数在区间上的最大值为M,最小值为N,则( )
A.14 B.12 C.10 D.8
变式2.若,则的最大值为( )
A. B. C.3 D.2
例7.已知函数存在最大值0,则a的值为( )
A.1 B.2 C.e D.
变式1.若函数在区间上有最小值,则实数取值范围是( )
A. B. C. D.
变式2.函数在上的最大值为2,则a的值为( )
A. B.2 C.5 D.
考点五:导数的构造法
例8.已知f(x)是定义在R上的偶函数,且,当时,,则不等式的解集为( )
A.(-∞,2)∪(2,+∞) B.(-∞,2)∪(0,2) C.(-2,0)∪(2,+∞) D.(-2,0)∪(0,2)
变式1.已知为偶函数,且,令,若时,,关于的不等式的解集为( )
A.或 B.
C. D.或
变式2.已知为定义在上的偶函数,其导函数为,对于任意的总有成立,则下列不等式成立的有( )
A.B.C.D.
例9.已知是可导的函数,且,则下列不等关系正确的是( )
A., B.,
C., D.,
变式1.设定义在上的函数的导函数为,若,,则不等式(其中为自然对数的底数)的解集为( )
A. B. C. D.
变式2.已知函数的定义域为,为的导函数.若,且,则不等式的解集为( )
A. B. C. D.
巩固练习
1.已知函数的导函数的图象如右图所示,那么函数的图象最有可能的是( )
2.函数的单调递减区间为( )
A. B. C. D.
3.函数的单调递减区间是( )
A. B. C. D.
4.已知函数的单调递减区间为,则的值为( )
A. B. C. D.
5.若函数在区间上单调递减,则实数的取值范围为( )
A. B. C. D.
6.若函数在是增函数,则实数a的取值范围是( )
A. B. C. D.
7.设函数,则的极大值点和极小值点分别为( )
A.-2,2 B.2,-2 C.5,-3 D.-5,3
8.已知函数,则在上的最小值为( )
A. B. C. D.
9.设,若函数有大于零的极值点,则的取值范围为( )
A. B. C. D.
10.已知函数在处取极大值,则( )
A.-2或-6 B.2或6 C.6 D.2
11.若函数 在上有最大值3,则该函数在上最小值( )
A. B.0 C. D.1
12.函数的极值点的个数是( )
A.0 B.1 C.2 D.3
13.已知时,函数取得极大值,则( )
A. B. C.4 D.2
14.上的函数满足:,,则不等式的解集为( )
A. B.
C. D.
15.已知定义在上的奇函数满足(),则( )
A. B.
C. D.
16.定义在上的函数的导函数为,若,则不等式的解集是( )
A. B. C. D.
6.2导数的应用答案
典例讲解
例1.C
变式1.B
变式2.A
例2.B
变式1.C
变式2.C
例3.D
变式1.B
变式2.A
例4.D
变式1.B
变式2.A
例5.A
变式1.B
变式2.B
例6.A
变式1.B
变式2.A
例7.D
变式1.C
变式2.B
例8.B
变式1.C
变式2.C
例9.C
变式1.C
变式2.A
巩固练习
1. A
2.D
3.B
4.B
5.B
6.C
7.A
8.D
9.A
10.C
11.C
12.C
13.B
14.D
15.B
16.D
11
