22.3.3二次函数中动态几何存在性问题类题通法 教案
文档属性
| 名称 | 22.3.3二次函数中动态几何存在性问题类题通法 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 79.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 16:02:47 | ||
图片预览

文档简介
二次函数中动态几何存在性问题
教学目标:
1. 初步学会由点的坐标表示线段长,由特殊几何特征转化为线段的数量关系,进而列方程解决问题;
通过具体二次函数动态几何存在性问题的分析,发展分析问题和解决问题的能力,体会类题通法;
初步学会这一类二次函数综合题的解题思路及解题步骤。
教学重点:学会这一类二次函数综合题的解题思路及解题步骤
教学难点:将特殊几何特征转化为线段的数量关系
教学过程:
一、复习回顾
1. 由点的坐标求线段长
(1)水平线段:横坐标之差的绝对值;
(2)铅垂线段:纵坐标之差的绝对值;
(3)斜线段:勾股定理(两点间距离公式)
2. 如何判断线段是水平或铅垂线段还是斜线段?(从点的坐标(数的角度)或从线段与坐标轴的位置关系(形的角度))
二、寻思路,明步骤
例题:如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
1.问题1:求该抛物线所对应的函数关系式及点D的坐标;
教学思路:
(1)用待定系数法可求该抛物线的函数关系式为y=-x2+2x+3,
(2)用配方法配方为y=-(x-1)2+4可得D(1,4)。
2.问题(2) 是否存在点P,使得PG=GF?若存在,求点P的坐标;若不存在,请说明理由.
教学思路:教师通过设计问题串,引导学生分析解决问题的思路,并共同完成答题过程。
(1)引导:
①线段PG、GF是属于哪类线段?
②我们可以用哪些点的坐标表示出线段PG、GF的长?
③如何表示点P、点G与点F的坐标?
④用代数式表示出线段PG、GF的长。
⑤根据什么列方程?
(2)小结思路:要求点P使得满足某一特殊几何特征(线段相等),由点的坐标表示出线段长,根据线段的数量关系列方程,解方程,最后检验求解。
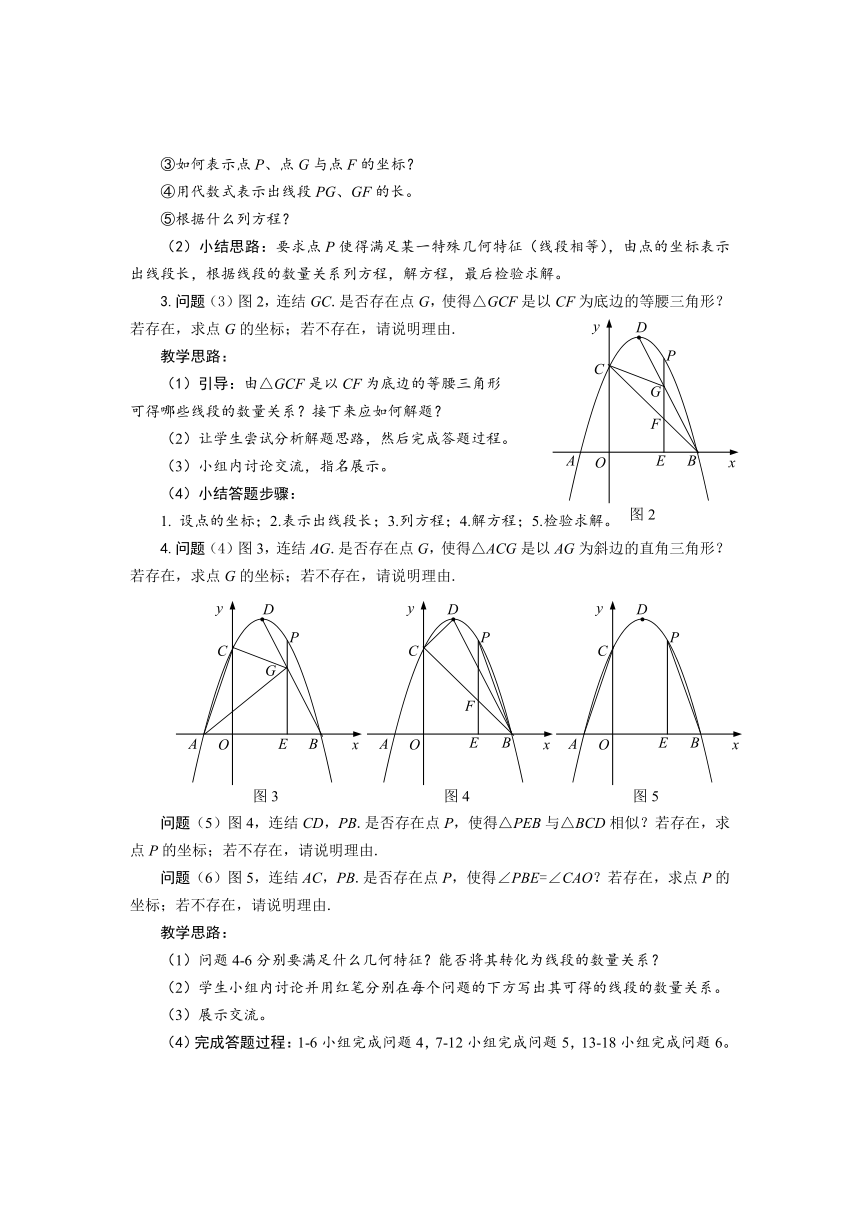
3.问题(3)图2,连结GC.是否存在点G,使得△GCF是以CF为底边的等腰三角形?若存在,求点G的坐标;若不存在,请说明理由.
教学思路:
(1)引导:由△GCF是以CF为底边的等腰三角形
可得哪些线段的数量关系?接下来应如何解题?
(2)让学生尝试分析解题思路,然后完成答题过程。
(3)小组内讨论交流,指名展示。
(4)小结答题步骤:
1. 设点的坐标;2.表示出线段长;3.列方程;4.解方程;5.检验求解。
4.问题(4)图3,连结AG.是否存在点G,使得△ACG是以AG为斜边的直角三角形?若存在,求点G的坐标;若不存在,请说明理由.
问题(5)图4,连结CD,PB.是否存在点P,使得△PEB与△BCD相似?若存在,求点P的坐标;若不存在,请说明理由.
问题(6)图5,连结AC,PB.是否存在点P,使得∠PBE=∠CAO?若存在,求点P的坐标;若不存在,请说明理由.
教学思路:
(1)问题4-6分别要满足什么几何特征?能否将其转化为线段的数量关系?
(2)学生小组内讨论并用红笔分别在每个问题的下方写出其可得的线段的数量关系。
(3)展示交流。
(4)完成答题过程:1-6小组完成问题4,7-12小组完成问题5,13-18小组完成问题6。独立完成后小组长检查,然后组织汇报交流。
(5)再次明确此类问题的解题思路和答题步骤。
三、小结提升
1. 二次函数中动态几何存在性问题的解题思路:
2. 解题的步骤是:一设,二表示,三列,四解,五求。
3. 这类二次函数的问题解题思路和答题步骤是相同的,我们叫做类题通法。
四、应用拓展
(海南中考.2020)抛物线y=x2+bx+c 经过点A (﹣3,0)和点B(2,0),与y轴交于点C.
(1)求该抛物线的函数表达式;
(2)点P为x轴下方抛物线上的动点,且位于y轴的左侧.
①如图6-1,过点P作PD⊥x轴于点D,作PE⊥y轴于点E,若PD=2PE时,
求PE的长;
②如图6-2,在直线AC上是否存在点P,使得∠ACP=∠OCB?若存在,请求出点P的坐标;若不存在,请说明理由.
y
O
x
C
AA
B
图1
D
F
E
P
G
y
O
x
C
AA
B
图2
D
F
E
P
G
y
O
x
C
AA
B
图5
D
E
P
y
O
x
C
AA
B
图3
D
E
P
G
y
O
x
C
AA
B
图4
D
F
E
P
转
化
特殊几何特征
线段的数量关系
点的坐标
表示线段长
列方程
解方程
检验求解
E
D
y
x
B
A
O
C
P
图6-1
图6-2
y
x
B
A
O
C
P
PAGE
教学目标:
1. 初步学会由点的坐标表示线段长,由特殊几何特征转化为线段的数量关系,进而列方程解决问题;
通过具体二次函数动态几何存在性问题的分析,发展分析问题和解决问题的能力,体会类题通法;
初步学会这一类二次函数综合题的解题思路及解题步骤。
教学重点:学会这一类二次函数综合题的解题思路及解题步骤
教学难点:将特殊几何特征转化为线段的数量关系
教学过程:
一、复习回顾
1. 由点的坐标求线段长
(1)水平线段:横坐标之差的绝对值;
(2)铅垂线段:纵坐标之差的绝对值;
(3)斜线段:勾股定理(两点间距离公式)
2. 如何判断线段是水平或铅垂线段还是斜线段?(从点的坐标(数的角度)或从线段与坐标轴的位置关系(形的角度))
二、寻思路,明步骤
例题:如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
1.问题1:求该抛物线所对应的函数关系式及点D的坐标;
教学思路:
(1)用待定系数法可求该抛物线的函数关系式为y=-x2+2x+3,
(2)用配方法配方为y=-(x-1)2+4可得D(1,4)。
2.问题(2) 是否存在点P,使得PG=GF?若存在,求点P的坐标;若不存在,请说明理由.
教学思路:教师通过设计问题串,引导学生分析解决问题的思路,并共同完成答题过程。
(1)引导:
①线段PG、GF是属于哪类线段?
②我们可以用哪些点的坐标表示出线段PG、GF的长?
③如何表示点P、点G与点F的坐标?
④用代数式表示出线段PG、GF的长。
⑤根据什么列方程?
(2)小结思路:要求点P使得满足某一特殊几何特征(线段相等),由点的坐标表示出线段长,根据线段的数量关系列方程,解方程,最后检验求解。
3.问题(3)图2,连结GC.是否存在点G,使得△GCF是以CF为底边的等腰三角形?若存在,求点G的坐标;若不存在,请说明理由.
教学思路:
(1)引导:由△GCF是以CF为底边的等腰三角形
可得哪些线段的数量关系?接下来应如何解题?
(2)让学生尝试分析解题思路,然后完成答题过程。
(3)小组内讨论交流,指名展示。
(4)小结答题步骤:
1. 设点的坐标;2.表示出线段长;3.列方程;4.解方程;5.检验求解。
4.问题(4)图3,连结AG.是否存在点G,使得△ACG是以AG为斜边的直角三角形?若存在,求点G的坐标;若不存在,请说明理由.
问题(5)图4,连结CD,PB.是否存在点P,使得△PEB与△BCD相似?若存在,求点P的坐标;若不存在,请说明理由.
问题(6)图5,连结AC,PB.是否存在点P,使得∠PBE=∠CAO?若存在,求点P的坐标;若不存在,请说明理由.
教学思路:
(1)问题4-6分别要满足什么几何特征?能否将其转化为线段的数量关系?
(2)学生小组内讨论并用红笔分别在每个问题的下方写出其可得的线段的数量关系。
(3)展示交流。
(4)完成答题过程:1-6小组完成问题4,7-12小组完成问题5,13-18小组完成问题6。独立完成后小组长检查,然后组织汇报交流。
(5)再次明确此类问题的解题思路和答题步骤。
三、小结提升
1. 二次函数中动态几何存在性问题的解题思路:
2. 解题的步骤是:一设,二表示,三列,四解,五求。
3. 这类二次函数的问题解题思路和答题步骤是相同的,我们叫做类题通法。
四、应用拓展
(海南中考.2020)抛物线y=x2+bx+c 经过点A (﹣3,0)和点B(2,0),与y轴交于点C.
(1)求该抛物线的函数表达式;
(2)点P为x轴下方抛物线上的动点,且位于y轴的左侧.
①如图6-1,过点P作PD⊥x轴于点D,作PE⊥y轴于点E,若PD=2PE时,
求PE的长;
②如图6-2,在直线AC上是否存在点P,使得∠ACP=∠OCB?若存在,请求出点P的坐标;若不存在,请说明理由.
y
O
x
C
AA
B
图1
D
F
E
P
G
y
O
x
C
AA
B
图2
D
F
E
P
G
y
O
x
C
AA
B
图5
D
E
P
y
O
x
C
AA
B
图3
D
E
P
G
y
O
x
C
AA
B
图4
D
F
E
P
转
化
特殊几何特征
线段的数量关系
点的坐标
表示线段长
列方程
解方程
检验求解
E
D
y
x
B
A
O
C
P
图6-1
图6-2
y
x
B
A
O
C
P
PAGE
同课章节目录
