沪科版数学七年级下册 10.3 平行线的性质 教案
文档属性
| 名称 | 沪科版数学七年级下册 10.3 平行线的性质 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 148.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-19 18:18:56 | ||
图片预览


文档简介
10.3 平行线的性质
【知识与技能】
1.会由平行线的性质1,简单推理得出性质2、性质3.
2.能运用平行线的性质和判定进行简单的推理.
【过程与方法】
通过探索平行线的性质的过程,培养学生严谨的逻辑推理能力和书写表达能力.
【情感态度】
有意识地引导学生积极参与到数学活动过程中,培养学生推理、应用能力.
【教学重点】
平行线性质的简单应用.
【教学难点】
平行线性质和判定的综合运用.
一、情境导入,初步认识
问题 前面我们学行线的几种判定方法,平行线有哪些性质呢?
【教学说明】教师提出问题,激发学生探求新知的兴趣.
二、思考探究,获取新知
1.平行线的性质1.
观察:如图,练习本上的横线都是相互平行的,从中任选两条分别记为AB,CD;画一条直线EF分别与AB,CD相交得8个角.
(1)任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?
(2)再任选一对同位角(如∠2与∠6),量一量它们的度数,它们的大小有什么关系?
由此你能得到什么结论?
【教学说明】教师提出问题,学生观察,动手实际操作,然后相互交流,得出结论.
【归纳结论】平行线有如下性质:
性质1 两条平行线被第三条直线所截,同位角相等.简单地说,两直线平行,同位角相等.
2.平行线的性质2、性质3.
思考:在上图中,当AB∥CD时,你还会发现内错角∠3和∠5的大小有什么关系?同旁内角∠4和∠5之间又有什么关系?能说明理由吗?
【教学说明】教师提出问题,学生独立思考,然后相互交流,发表各自的见解,学生很容易借助性质1,得出性质2、性质3.
【归纳结论】由平行线的性质1,可以推得平行线的另外两个性质:
性质2 两条平行线被第三条直线所截,内错角相等.简单地说,两直线平行,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.简单地说,两直线平行,同旁内角互补.
三、典例精析,掌握新知
例1 如图,直线AB,CD,EF被MN所截,∠1=∠2,AB∥EF,那么CD∥EF吗?∠2与∠3有什么数量关系?∠2与∠4有什么数量关系?
【解】CD∥EF,∠2+∠3=180°,∠2=∠4.
理由如下:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
∵AB∥EF.
∴CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∴∠2=∠4(两直线平行,内错角相等).
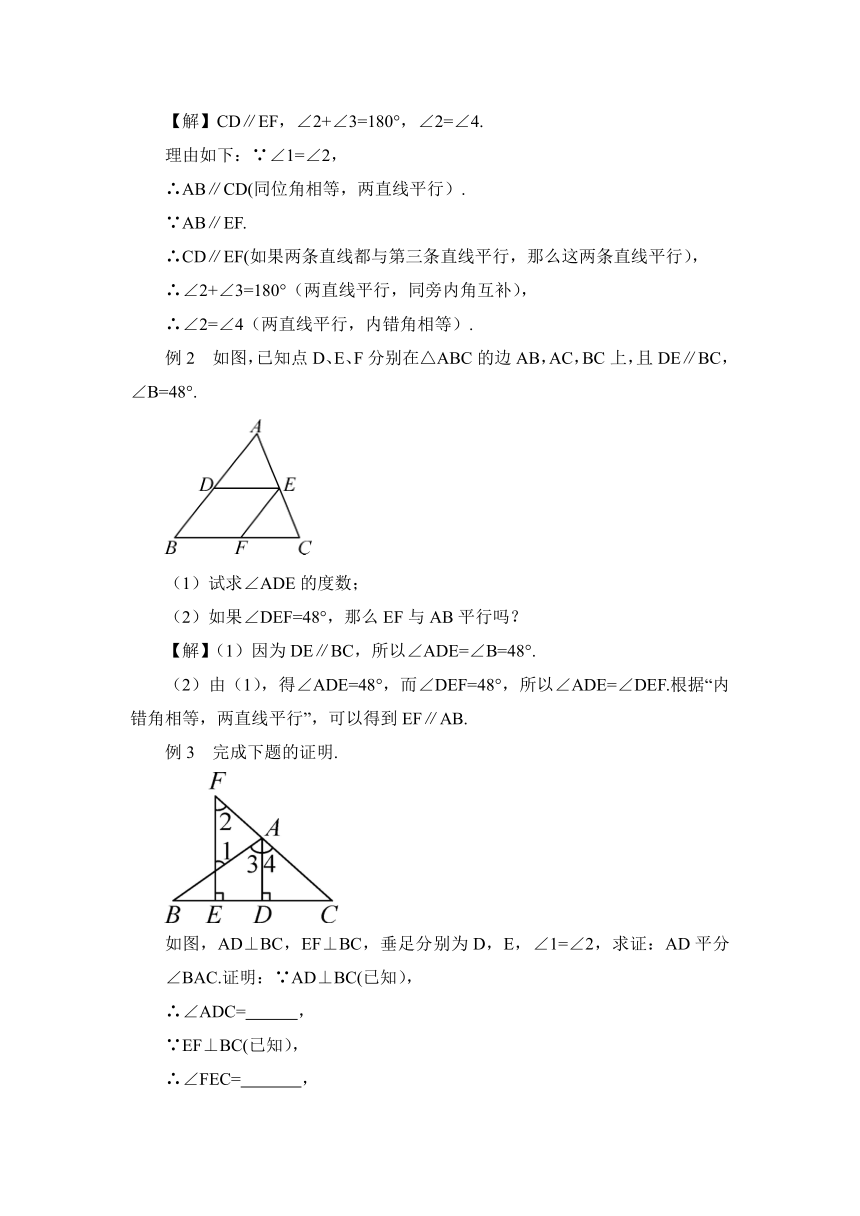
例2 如图,已知点D、E、F分别在△ABC的边AB,AC,BC上,且DE∥BC,∠B=48°.
(1)试求∠ADE的度数;
(2)如果∠DEF=48°,那么EF与AB平行吗?
【解】(1)因为DE∥BC,所以∠ADE=∠B=48°.
(2)由(1),得∠ADE=48°,而∠DEF=48°,所以∠ADE=∠DEF.根据“内错角相等,两直线平行”,可以得到EF∥AB.
例3 完成下题的证明.
如图,AD⊥BC,EF⊥BC,垂足分别为D,E,∠1=∠2,求证:AD平分∠BAC.证明:∵AD⊥BC(已知),
∴∠ADC= ,
∵EF⊥BC(已知),
∴∠FEC= ,
∴∠ADC=∠FEC,
∴AD∥ ( );
∴∠1= ( ),
∠2= ( ),
又∵∠1=∠2(已知),
∴∠3=∠ ,
∴AD平分∠BAC.
【教学说明】老师给出例题,学生独立自主完成,老师也可让几个学生上台在黑板上演算或解答,然后给予点评.
四、运用新知,深化理解
1.看图填空.
(1)由DE∥BC,可以得到∠ADE= ,依据是 .
(2)由DE∥BC,可以得到∠DFB= .依据是 .
(3)由DE∥BC,可以得到∠C+ =180°,依据是 .
(4)由DF∥AC,可以得到∠AED= ,依据是 .
(5)由DF∥AC,可以得到∠C= .依据是 .
2.如图,直线AB∥CD,直线EF分别交AB于点E,交CD于点F,直线∠AEF=90°,求∠DFE的度数,由此你能得到直线EF与直线CD有怎样的位置关系?
3.如图,在四边形ABCD中,AD∥BC,∠C=71°.试求∠D的度数.
【教学说明】教师给出习题,学生独立自主完成,教师巡视,对解题过程中出现的问题及时予以指正,对有困难的学生进行点拨.
【答案】1.(1)∠B,两直线平行,同位角相等.
(2)∠EDF,两直线平行,内错角相等.
(3)∠DEC,两直线平行,同旁内角互补.
(4)∠EDF,两直线平行,内错角相等.
(5)∠DFB,两直线平行,同位角相等.
2.∵AB∥CD
∴∠DFE=∠AEF=90°(两直线平行,内错角相等)
∴EF⊥CD.
3.∵AD∥BC
∴∠C+∠D=180°(两直线平行,同旁内角互补)
∴∠D=180°-∠C=180°-71°=109°.
五、师生互动,课堂小结
通过这节课的学习,你掌握了哪些新知识?还有哪些疑问?请与同伴交流.
【教学说明】学生相互交流,回顾平行线的性质定理,加深对所学新知识的理解和运用.
完成练习册中本课时 练习.
【知识与技能】
1.会由平行线的性质1,简单推理得出性质2、性质3.
2.能运用平行线的性质和判定进行简单的推理.
【过程与方法】
通过探索平行线的性质的过程,培养学生严谨的逻辑推理能力和书写表达能力.
【情感态度】
有意识地引导学生积极参与到数学活动过程中,培养学生推理、应用能力.
【教学重点】
平行线性质的简单应用.
【教学难点】
平行线性质和判定的综合运用.
一、情境导入,初步认识
问题 前面我们学行线的几种判定方法,平行线有哪些性质呢?
【教学说明】教师提出问题,激发学生探求新知的兴趣.
二、思考探究,获取新知
1.平行线的性质1.
观察:如图,练习本上的横线都是相互平行的,从中任选两条分别记为AB,CD;画一条直线EF分别与AB,CD相交得8个角.
(1)任选一对同位角(如∠1与∠5),量一量它们的度数,它们的大小有什么关系?
(2)再任选一对同位角(如∠2与∠6),量一量它们的度数,它们的大小有什么关系?
由此你能得到什么结论?
【教学说明】教师提出问题,学生观察,动手实际操作,然后相互交流,得出结论.
【归纳结论】平行线有如下性质:
性质1 两条平行线被第三条直线所截,同位角相等.简单地说,两直线平行,同位角相等.
2.平行线的性质2、性质3.
思考:在上图中,当AB∥CD时,你还会发现内错角∠3和∠5的大小有什么关系?同旁内角∠4和∠5之间又有什么关系?能说明理由吗?
【教学说明】教师提出问题,学生独立思考,然后相互交流,发表各自的见解,学生很容易借助性质1,得出性质2、性质3.
【归纳结论】由平行线的性质1,可以推得平行线的另外两个性质:
性质2 两条平行线被第三条直线所截,内错角相等.简单地说,两直线平行,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.简单地说,两直线平行,同旁内角互补.
三、典例精析,掌握新知
例1 如图,直线AB,CD,EF被MN所截,∠1=∠2,AB∥EF,那么CD∥EF吗?∠2与∠3有什么数量关系?∠2与∠4有什么数量关系?
【解】CD∥EF,∠2+∠3=180°,∠2=∠4.
理由如下:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
∵AB∥EF.
∴CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线平行),
∴∠2+∠3=180°(两直线平行,同旁内角互补),
∴∠2=∠4(两直线平行,内错角相等).
例2 如图,已知点D、E、F分别在△ABC的边AB,AC,BC上,且DE∥BC,∠B=48°.
(1)试求∠ADE的度数;
(2)如果∠DEF=48°,那么EF与AB平行吗?
【解】(1)因为DE∥BC,所以∠ADE=∠B=48°.
(2)由(1),得∠ADE=48°,而∠DEF=48°,所以∠ADE=∠DEF.根据“内错角相等,两直线平行”,可以得到EF∥AB.
例3 完成下题的证明.
如图,AD⊥BC,EF⊥BC,垂足分别为D,E,∠1=∠2,求证:AD平分∠BAC.证明:∵AD⊥BC(已知),
∴∠ADC= ,
∵EF⊥BC(已知),
∴∠FEC= ,
∴∠ADC=∠FEC,
∴AD∥ ( );
∴∠1= ( ),
∠2= ( ),
又∵∠1=∠2(已知),
∴∠3=∠ ,
∴AD平分∠BAC.
【教学说明】老师给出例题,学生独立自主完成,老师也可让几个学生上台在黑板上演算或解答,然后给予点评.
四、运用新知,深化理解
1.看图填空.
(1)由DE∥BC,可以得到∠ADE= ,依据是 .
(2)由DE∥BC,可以得到∠DFB= .依据是 .
(3)由DE∥BC,可以得到∠C+ =180°,依据是 .
(4)由DF∥AC,可以得到∠AED= ,依据是 .
(5)由DF∥AC,可以得到∠C= .依据是 .
2.如图,直线AB∥CD,直线EF分别交AB于点E,交CD于点F,直线∠AEF=90°,求∠DFE的度数,由此你能得到直线EF与直线CD有怎样的位置关系?
3.如图,在四边形ABCD中,AD∥BC,∠C=71°.试求∠D的度数.
【教学说明】教师给出习题,学生独立自主完成,教师巡视,对解题过程中出现的问题及时予以指正,对有困难的学生进行点拨.
【答案】1.(1)∠B,两直线平行,同位角相等.
(2)∠EDF,两直线平行,内错角相等.
(3)∠DEC,两直线平行,同旁内角互补.
(4)∠EDF,两直线平行,内错角相等.
(5)∠DFB,两直线平行,同位角相等.
2.∵AB∥CD
∴∠DFE=∠AEF=90°(两直线平行,内错角相等)
∴EF⊥CD.
3.∵AD∥BC
∴∠C+∠D=180°(两直线平行,同旁内角互补)
∴∠D=180°-∠C=180°-71°=109°.
五、师生互动,课堂小结
通过这节课的学习,你掌握了哪些新知识?还有哪些疑问?请与同伴交流.
【教学说明】学生相互交流,回顾平行线的性质定理,加深对所学新知识的理解和运用.
完成练习册中本课时 练习.
