沪科版数学七年级下册 8.3 完全平方公式与平方差公式 教案(表格式)
文档属性
| 名称 | 沪科版数学七年级下册 8.3 完全平方公式与平方差公式 教案(表格式) | 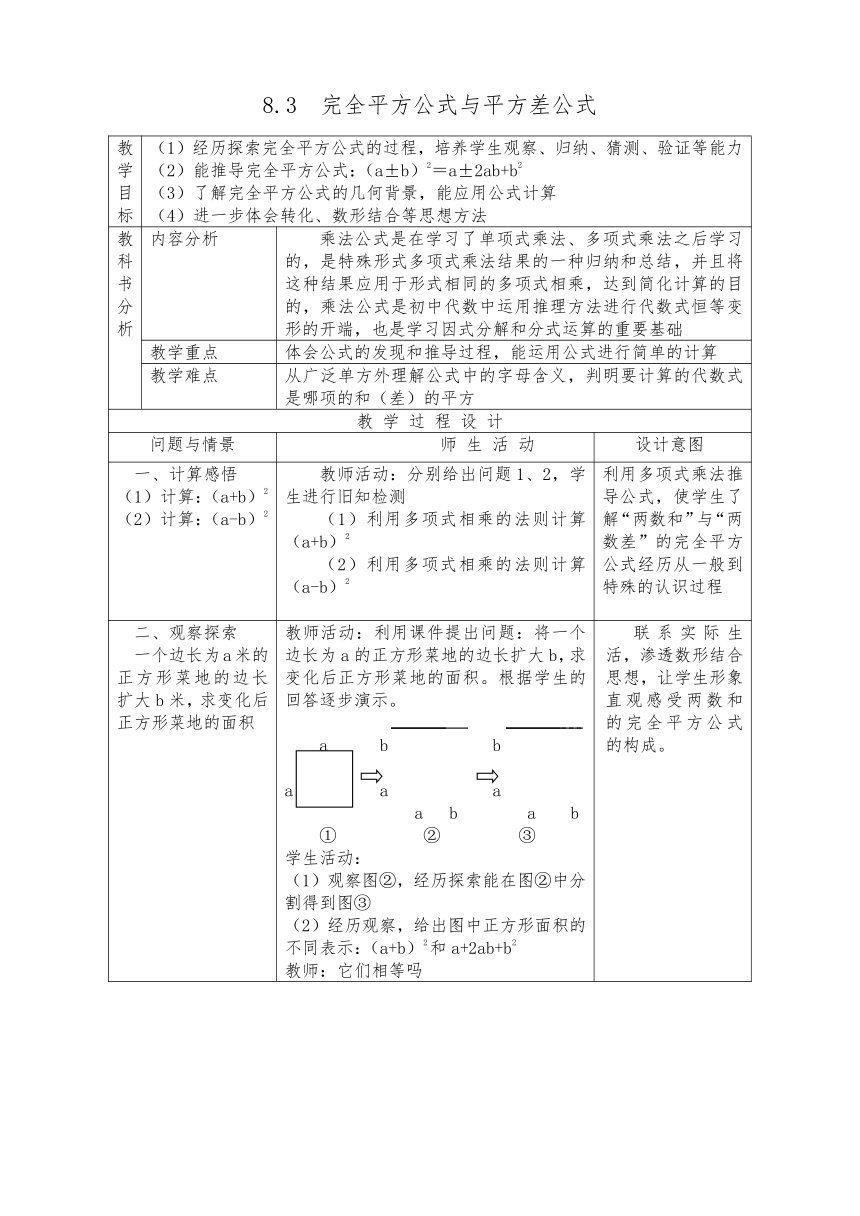 | |
| 格式 | docx | ||
| 文件大小 | 18.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-20 21:20:57 | ||
图片预览

文档简介
8.3 完全平方公式与平方差公式
教 学 目 标 (1)经历探索完全平方公式的过程,培养学生观察、归纳、猜测、验证等能力 (2)能推导完全平方公式:(a±b)2=a±2ab+b2 (3)了解完全平方公式的几何背景,能应用公式计算 (4)进一步体会转化、数形结合等思想方法
教 科 书 分 析 内容分析 乘法公式是在学习了单项式乘法、多项式乘法之后学习的,是特殊形式多项式乘法结果的一种归纳和总结,并且将这种结果应用于形式相同的多项式相乘,达到简化计算的目的,乘法公式是初中代数中运用推理方法进行代数式恒等变形的开端,也是学习因式分解和分式运算的重要基础
教学重点 体会公式的发现和推导过程,能运用公式进行简单的计算
教学难点 从广泛单方外理解公式中的字母含义,判明要计算的代数式是哪项的和(差)的平方
教 学 过 程 设 计
问题与情景 师 生 活 动 设计意图
一、计算感悟 (1)计算:(a+b)2 (2)计算:(a-b)2 教师活动:分别给出问题1、2,学生进行旧知检测 (1)利用多项式相乘的法则计算(a+b)2 (2)利用多项式相乘的法则计算(a-b)2 利用多项式乘法推导公式,使学生了解“两数和”与“两数差”的完全平方公式经历从一般到特殊的认识过程
二、观察探索 一个边长为a米的正方形菜地的边长扩大b米,求变化后正方形菜地的面积 教师活动:利用课件提出问题:将一个边长为a的正方形菜地的边长扩大b,求变化后正方形菜地的面积。根据学生的回答逐步演示。 a b b a a a a b a b ① ② ③ 学生活动: (1)观察图②,经历探索能在图②中分割得到图③ (2)经历观察,给出图中正方形面积的不同表示:(a+b)2和a+2ab+b2 教师:它们相等吗 联系实际生活,渗透数形结合思想,让学生形象直观感受两数和的完全平方公式的构成。
三、归纳总结 用数学语言和方案语言总结、归纳完全平方公式。在(a+b)2=a+2ab+b2中将b换成-b,就得到了完全平方差公式。 教师活动:引导学生归纳完全平方公式 学生活动: (a+b)2=a+2ab+b2 (a-b)2=a-2ab+b2 这两个公式叫做完全平方公式用语言表述是:两数和(或差)的平方,等于这两数的平方和,加上(或减去)这两个数乘积的两倍 师生共同明晰公式,总结口诀:“首平方,尾平方,乘积两倍中间放,符号和前一个样”
四、例题解析 例1 利用乘法公式计算: (1)(2x+3)2 (2)(3a-2b)2 教师活动:分步演示计算过程 (1)(2x+3)2=(2x)2+2·2x·3+32 (a+b)2=a+2ab+b2 =4x2+12x+9 (2) (3a-2b)2=(3a)2-2·3a·2b +(2b) 2 (a-b)2=a2-2ab+b2 = 9a2-12ab+4b2 学生活动: 学习完全平方公式的应用,明确字母a、b在具体式子中分别表示什么 本例解析时采用了对比的方式,比较直观的指出公式中字母a、b在具体式子中分别表示什么,明确字母意义的广泛性,有利于学生掌握和应用公式
五、巩固练习 1、利用乘法公式计算: (1)(3y+4)2 (2)(b-2a)2 (3) (-m+)2 (4) (-x-2)2 教师活动: (1)给出问题1,鼓励学生独立完成 (2)针对问题1中的(3)(4)要做出说明,可以直接应用完全平方公式计算,也可以变形为( - m)2或[(m - )2 ]和(x+2)2,再应用完全平方公式计算 学生活动: (1)明确各题中的字母a、b分别表示什么,利用完全平方公式计算 (2)针对问题1中的(3)和(4),想想有没有其他的作法 问题1中的(1)和(2)设计学生会操作的问题,帮助学生熟悉公式的直接应用;设计(3)和(4),引导学生探索问题的恒等变形,
六、目标回顾 教师活动: 请同学们回顾本节课学习了哪些内容?有哪些收获 学生活动:经历思考和讨论后,用自己的语言回答 旨在让学生反思自己的学习过程,梳理本节课的知识,并将所学的知识进行延伸和拓展
七、作业设计 1、必做作业: 课本第69页的练习第1题2、4小题和第71页的习题8.3的第1题 2、选做作业: 已知x+y=3,xy=1,求x2+y2 设计分层作业,使不同的学生在数学上得到不同的发展
教 学 目 标 (1)经历探索完全平方公式的过程,培养学生观察、归纳、猜测、验证等能力 (2)能推导完全平方公式:(a±b)2=a±2ab+b2 (3)了解完全平方公式的几何背景,能应用公式计算 (4)进一步体会转化、数形结合等思想方法
教 科 书 分 析 内容分析 乘法公式是在学习了单项式乘法、多项式乘法之后学习的,是特殊形式多项式乘法结果的一种归纳和总结,并且将这种结果应用于形式相同的多项式相乘,达到简化计算的目的,乘法公式是初中代数中运用推理方法进行代数式恒等变形的开端,也是学习因式分解和分式运算的重要基础
教学重点 体会公式的发现和推导过程,能运用公式进行简单的计算
教学难点 从广泛单方外理解公式中的字母含义,判明要计算的代数式是哪项的和(差)的平方
教 学 过 程 设 计
问题与情景 师 生 活 动 设计意图
一、计算感悟 (1)计算:(a+b)2 (2)计算:(a-b)2 教师活动:分别给出问题1、2,学生进行旧知检测 (1)利用多项式相乘的法则计算(a+b)2 (2)利用多项式相乘的法则计算(a-b)2 利用多项式乘法推导公式,使学生了解“两数和”与“两数差”的完全平方公式经历从一般到特殊的认识过程
二、观察探索 一个边长为a米的正方形菜地的边长扩大b米,求变化后正方形菜地的面积 教师活动:利用课件提出问题:将一个边长为a的正方形菜地的边长扩大b,求变化后正方形菜地的面积。根据学生的回答逐步演示。 a b b a a a a b a b ① ② ③ 学生活动: (1)观察图②,经历探索能在图②中分割得到图③ (2)经历观察,给出图中正方形面积的不同表示:(a+b)2和a+2ab+b2 教师:它们相等吗 联系实际生活,渗透数形结合思想,让学生形象直观感受两数和的完全平方公式的构成。
三、归纳总结 用数学语言和方案语言总结、归纳完全平方公式。在(a+b)2=a+2ab+b2中将b换成-b,就得到了完全平方差公式。 教师活动:引导学生归纳完全平方公式 学生活动: (a+b)2=a+2ab+b2 (a-b)2=a-2ab+b2 这两个公式叫做完全平方公式用语言表述是:两数和(或差)的平方,等于这两数的平方和,加上(或减去)这两个数乘积的两倍 师生共同明晰公式,总结口诀:“首平方,尾平方,乘积两倍中间放,符号和前一个样”
四、例题解析 例1 利用乘法公式计算: (1)(2x+3)2 (2)(3a-2b)2 教师活动:分步演示计算过程 (1)(2x+3)2=(2x)2+2·2x·3+32 (a+b)2=a+2ab+b2 =4x2+12x+9 (2) (3a-2b)2=(3a)2-2·3a·2b +(2b) 2 (a-b)2=a2-2ab+b2 = 9a2-12ab+4b2 学生活动: 学习完全平方公式的应用,明确字母a、b在具体式子中分别表示什么 本例解析时采用了对比的方式,比较直观的指出公式中字母a、b在具体式子中分别表示什么,明确字母意义的广泛性,有利于学生掌握和应用公式
五、巩固练习 1、利用乘法公式计算: (1)(3y+4)2 (2)(b-2a)2 (3) (-m+)2 (4) (-x-2)2 教师活动: (1)给出问题1,鼓励学生独立完成 (2)针对问题1中的(3)(4)要做出说明,可以直接应用完全平方公式计算,也可以变形为( - m)2或[(m - )2 ]和(x+2)2,再应用完全平方公式计算 学生活动: (1)明确各题中的字母a、b分别表示什么,利用完全平方公式计算 (2)针对问题1中的(3)和(4),想想有没有其他的作法 问题1中的(1)和(2)设计学生会操作的问题,帮助学生熟悉公式的直接应用;设计(3)和(4),引导学生探索问题的恒等变形,
六、目标回顾 教师活动: 请同学们回顾本节课学习了哪些内容?有哪些收获 学生活动:经历思考和讨论后,用自己的语言回答 旨在让学生反思自己的学习过程,梳理本节课的知识,并将所学的知识进行延伸和拓展
七、作业设计 1、必做作业: 课本第69页的练习第1题2、4小题和第71页的习题8.3的第1题 2、选做作业: 已知x+y=3,xy=1,求x2+y2 设计分层作业,使不同的学生在数学上得到不同的发展
