人教A版高中数学必修第一册第二章 复习与检测学案(Word无答案)
文档属性
| 名称 | 人教A版高中数学必修第一册第二章 复习与检测学案(Word无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 74.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-20 14:54:33 | ||
图片预览

文档简介
第二章 复习与检测
一 、本章核心知识评价要求
主题 知识单元 核心知识 评价要求
了解 理解 掌握
预 备 知 识 一元二次函数、方程和不等式 等式和不等式的性质 不等式的概念 √
不等式的性质 √
基本不等式 基本不等式及其应用 √
二次函数与一元二次方程、不等式 一元二次不等式的概念 √
二次函数的零点 √
一元二次不等式与相应函数、方程的关系 √
一元二次不等式的解法 √
知识梳理
知识点1 不等式的性质
不等式的基本性质
(1)对称性:a>b . (2)传递性:a>b,b>c .
(3)可加性:a>b . (4)可乘性:a>b,c>0 . ;a>b,c<0 .
(5)加法法则:a>b,c>d . (6)乘法法则:a>b>0,c>d>0 .
(7)乘方法则:a>b>0 . .
例1.如果a,b,c满足c<b<a且ac<0,则以下列选项中不一定成立的是( )
A.ab>ac B.c(b-a)>0 C.cb2<ab2 D.ac(a-c)<0
知识点二 基本不等式
1.重要不等式: a,b∈R,有a2+b2 ≥ . ,当且仅当 . 时,等号成立.
2.基本不等式:当a,b是任意正实数时,a,b的几何平均数不大于它们的算术平均数,即 . ,当且仅当 . 时,等号成立.
3.已知x、y都是正数,(1)若x+y=S(和为定值),则当x=y时,积xy取得最 . 值 . 。
(2)若xy=p(积为定值),则当x=y时,和x+y取得最 . 值 . 。
上述命题可归纳为口诀:积定和最小,和定积最大.
例题2:设x>-1,求y=的最小值.
变式:设x<-1,求y=的最大值.
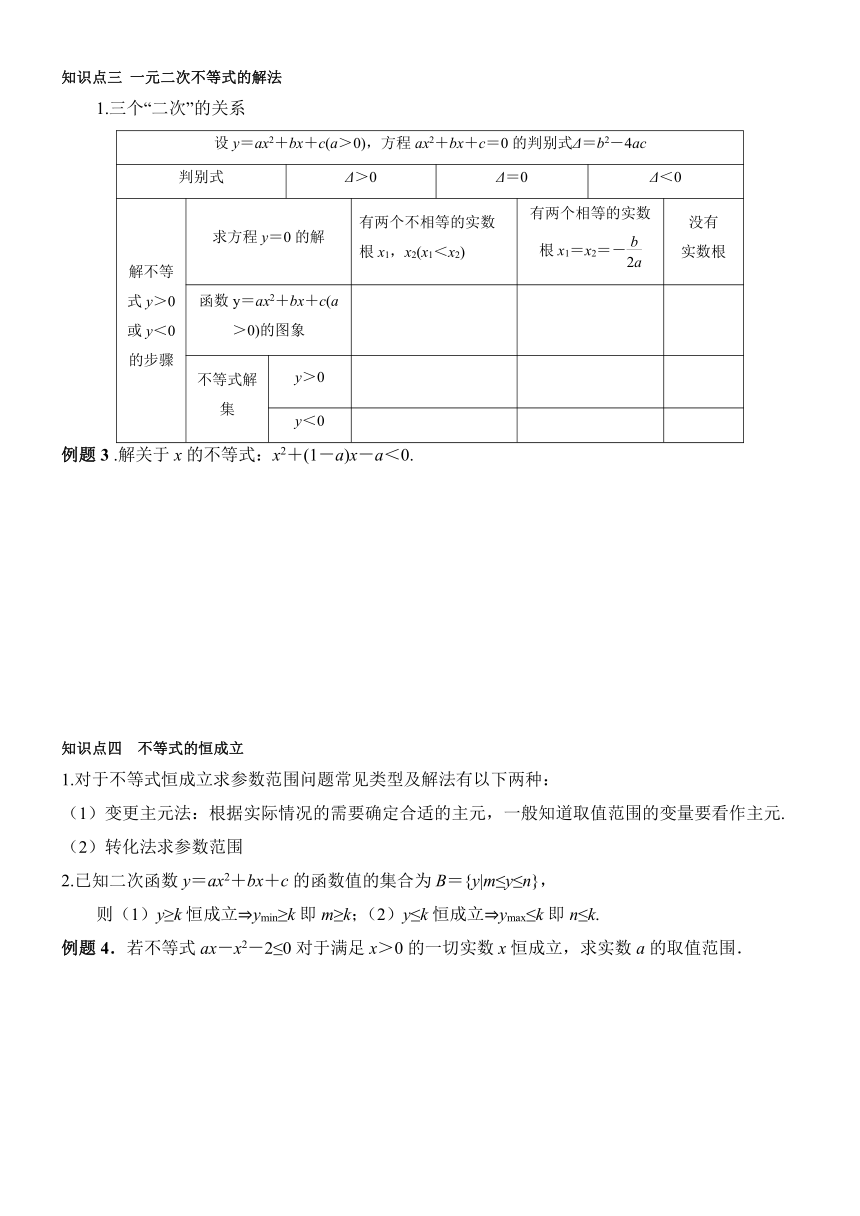
知识点三 一元二次不等式的解法
1.三个“二次”的关系
设y=ax2+bx+c(a>0),方程ax2+bx+c=0的判别式Δ=b2-4ac
判别式 Δ>0 Δ=0 Δ<0
解不等式y>0或y<0的步骤 求方程y=0的解 有两个不相等的实数根x1,x2(x1<x2) 有两个相等的实数根x1=x2=- 没有 实数根
函数y=ax2+bx+c(a>0)的图象
不等式解集 y>0
y<0
例题3 .解关于x的不等式:x2+(1-a)x-a<0.
知识点四 不等式的恒成立
1.对于不等式恒成立求参数范围问题常见类型及解法有以下两种:
(1)变更主元法:根据实际情况的需要确定合适的主元,一般知道取值范围的变量要看作主元.
(2)转化法求参数范围
2.已知二次函数y=ax2+bx+c的函数值的集合为B={y|m≤y≤n},
则(1)y≥k恒成立 ymin≥k即m≥k;(2)y≤k恒成立 ymax≤k即n≤k.
例题4.若不等式ax-x2-2≤0对于满足x>0的一切实数x恒成立,求实数a的取值范围.
三、 易错点分析
易错一 基本不等式求最值满足“一正二定三相等”。
例题5.已知x<3,求f(x)=+x的最大值;
易错二 解不等式时易忽略对参数的讨论
例题6.解关于x的不等式:ax2-2 ≥ 2x-ax.
变式:解关于x的不等式:ax2-2 ≥ 2x-ax.
四、巩固练习
1、设,则下列命题正确的是:( )
A.若 则 B..若 则 C.若 则 D.若 则
2、设,则是的( )条件。
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件
3、设,则有( )
A. B. C. D.
4、若,则下列不等式成立的是( )
A. B. C. D.
5、一元二次不等式的解集是: 。
6、已知命题P:,若命题P是假命题,则实数的取值范围是: 。
7、已知,若,则的最大值是 ,此时 , 。
8、若不等式的解集为,则 。
9、已知二次函数,
(1)当时,解不等式
(2)若,的解集为,求的最小值。
10、中欧班列是推进与“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设。目前车站准备在某仓库外,利用其一侧原有墙体,建造一间墙高为3m,底面积为12㎡,且背面靠墙的长方体形状的保管员室。由于此保管员室的后背靠墙,无需建造费用,因此甲工程队给出的报价为:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体报价为每平方米150元,屋顶和地面以及其他报价共计7200元。设屋子的左右两侧墙的长度均为xm(2≤x≤6).
(1)当左右两面墙的长度为多少时,甲工程队报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元(),若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,试求的取值范围。
一 、本章核心知识评价要求
主题 知识单元 核心知识 评价要求
了解 理解 掌握
预 备 知 识 一元二次函数、方程和不等式 等式和不等式的性质 不等式的概念 √
不等式的性质 √
基本不等式 基本不等式及其应用 √
二次函数与一元二次方程、不等式 一元二次不等式的概念 √
二次函数的零点 √
一元二次不等式与相应函数、方程的关系 √
一元二次不等式的解法 √
知识梳理
知识点1 不等式的性质
不等式的基本性质
(1)对称性:a>b . (2)传递性:a>b,b>c .
(3)可加性:a>b . (4)可乘性:a>b,c>0 . ;a>b,c<0 .
(5)加法法则:a>b,c>d . (6)乘法法则:a>b>0,c>d>0 .
(7)乘方法则:a>b>0 . .
例1.如果a,b,c满足c<b<a且ac<0,则以下列选项中不一定成立的是( )
A.ab>ac B.c(b-a)>0 C.cb2<ab2 D.ac(a-c)<0
知识点二 基本不等式
1.重要不等式: a,b∈R,有a2+b2 ≥ . ,当且仅当 . 时,等号成立.
2.基本不等式:当a,b是任意正实数时,a,b的几何平均数不大于它们的算术平均数,即 . ,当且仅当 . 时,等号成立.
3.已知x、y都是正数,(1)若x+y=S(和为定值),则当x=y时,积xy取得最 . 值 . 。
(2)若xy=p(积为定值),则当x=y时,和x+y取得最 . 值 . 。
上述命题可归纳为口诀:积定和最小,和定积最大.
例题2:设x>-1,求y=的最小值.
变式:设x<-1,求y=的最大值.
知识点三 一元二次不等式的解法
1.三个“二次”的关系
设y=ax2+bx+c(a>0),方程ax2+bx+c=0的判别式Δ=b2-4ac
判别式 Δ>0 Δ=0 Δ<0
解不等式y>0或y<0的步骤 求方程y=0的解 有两个不相等的实数根x1,x2(x1<x2) 有两个相等的实数根x1=x2=- 没有 实数根
函数y=ax2+bx+c(a>0)的图象
不等式解集 y>0
y<0
例题3 .解关于x的不等式:x2+(1-a)x-a<0.
知识点四 不等式的恒成立
1.对于不等式恒成立求参数范围问题常见类型及解法有以下两种:
(1)变更主元法:根据实际情况的需要确定合适的主元,一般知道取值范围的变量要看作主元.
(2)转化法求参数范围
2.已知二次函数y=ax2+bx+c的函数值的集合为B={y|m≤y≤n},
则(1)y≥k恒成立 ymin≥k即m≥k;(2)y≤k恒成立 ymax≤k即n≤k.
例题4.若不等式ax-x2-2≤0对于满足x>0的一切实数x恒成立,求实数a的取值范围.
三、 易错点分析
易错一 基本不等式求最值满足“一正二定三相等”。
例题5.已知x<3,求f(x)=+x的最大值;
易错二 解不等式时易忽略对参数的讨论
例题6.解关于x的不等式:ax2-2 ≥ 2x-ax.
变式:解关于x的不等式:ax2-2 ≥ 2x-ax.
四、巩固练习
1、设,则下列命题正确的是:( )
A.若 则 B..若 则 C.若 则 D.若 则
2、设,则是的( )条件。
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分又不必要条件
3、设,则有( )
A. B. C. D.
4、若,则下列不等式成立的是( )
A. B. C. D.
5、一元二次不等式的解集是: 。
6、已知命题P:,若命题P是假命题,则实数的取值范围是: 。
7、已知,若,则的最大值是 ,此时 , 。
8、若不等式的解集为,则 。
9、已知二次函数,
(1)当时,解不等式
(2)若,的解集为,求的最小值。
10、中欧班列是推进与“一带一路”沿线国家道路联通、贸易畅通的重要举措,作为中欧铁路在东北地区的始发站,沈阳某火车站正在不断建设。目前车站准备在某仓库外,利用其一侧原有墙体,建造一间墙高为3m,底面积为12㎡,且背面靠墙的长方体形状的保管员室。由于此保管员室的后背靠墙,无需建造费用,因此甲工程队给出的报价为:屋子前面新建墙体的报价为每平方米400元,左右两面新建墙体报价为每平方米150元,屋顶和地面以及其他报价共计7200元。设屋子的左右两侧墙的长度均为xm(2≤x≤6).
(1)当左右两面墙的长度为多少时,甲工程队报价最低?
(2)现有乙工程队也参与此保管员室建造竞标,其给出的整体报价为元(),若无论左右两面墙的长度为多少米,乙工程队都能竞标成功,试求的取值范围。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
