北师大版(2019)高中数学 必修第二册 2.1从位移的合成到向量的加减法 课件(共17张PPT)
文档属性
| 名称 | 北师大版(2019)高中数学 必修第二册 2.1从位移的合成到向量的加减法 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 422.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-20 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
§2.1从位移的合成到向量的加减法
北师大版(2017版)高中数学必修第二册第二章
第一课时 向量的加法
掌握向量加法的概念;能熟练运用三角形法则和平行四边形法则做几个向量的和向量;能准确表述向量加法的交换律和结合律,并能熟练运用它们进行向量计算.
学习目标:
学习重点难度
教学重点: 向量加法的概念和向量加法的法则及运算律.
教学难点: 向量加法的运算.
(一)创设情境
问题1:小明从A到B,再从B按原方向到C,
则两次的位移和:
问题2:若上题改为从A到B,再从B按反方向到C,
则两次的位移和:
问题3:某车从A到B,再从B改变方向到C,
则两次的位移和:
A
B
C
A
A
B
B
C
C
a
b
A
C
B
(二)新课探究
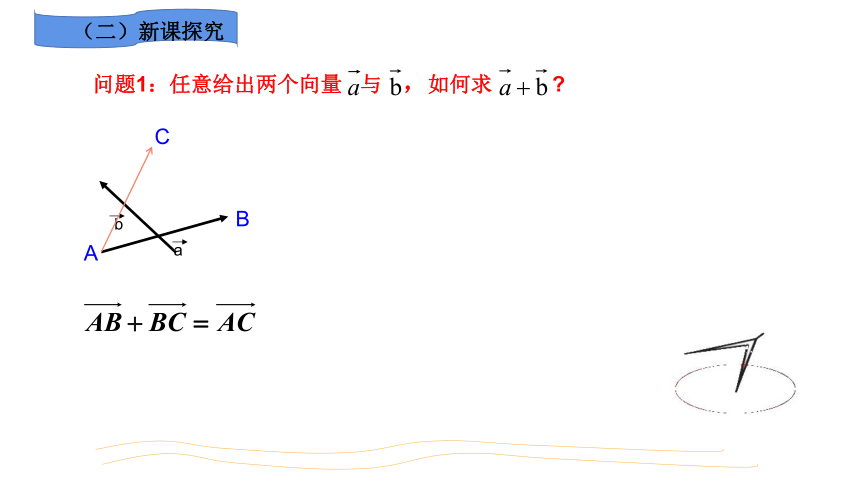
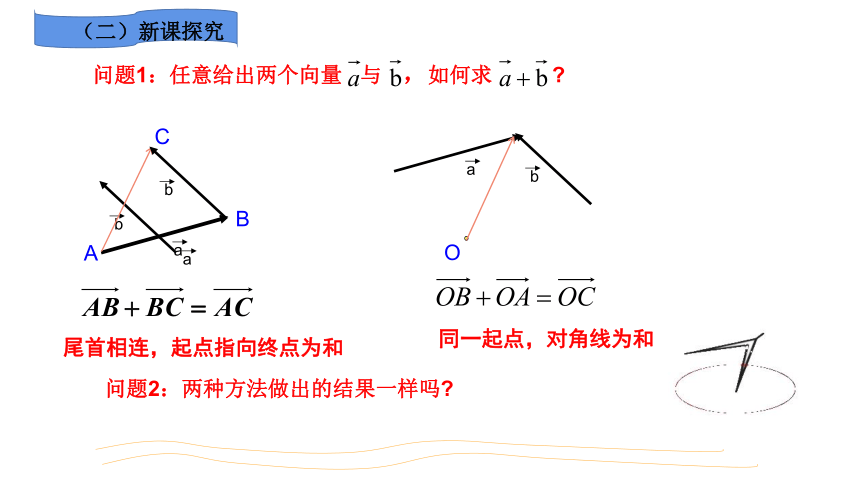
问题1:任意给出两个向量 与 ,如何求
O
问题2:两种方法做出的结果一样吗
a
a
b
b
A
C
B
b
a
(二)新课探究
尾首相连,起点指向终点为和
同一起点,对角线为和
问题1:任意给出两个向量 与 ,如何求
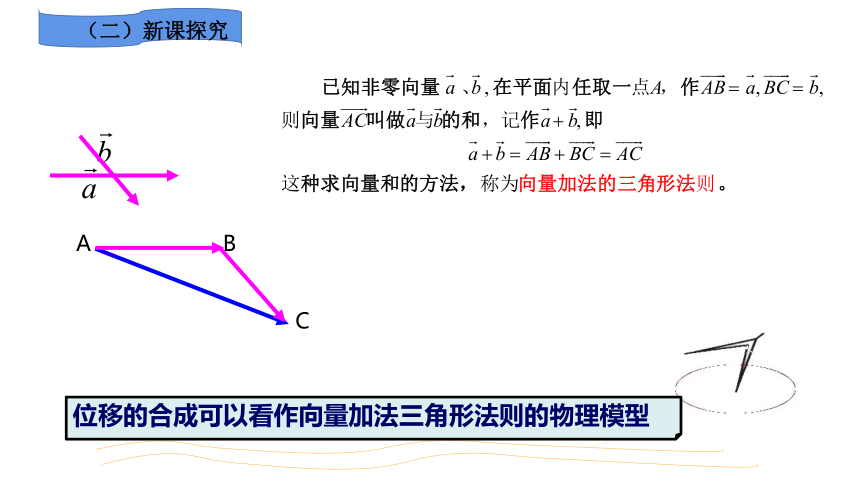
位移的合成可以看作向量加法三角形法则的物理模型
(二)新课探究
C
A
B
A
B
C
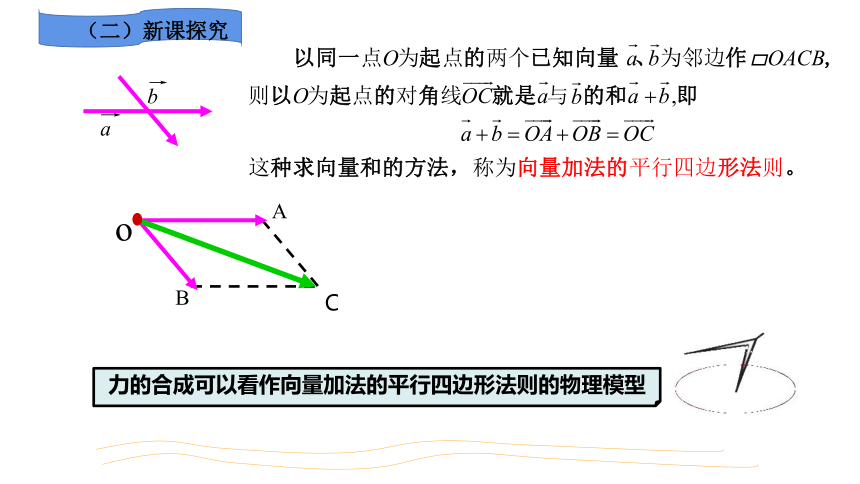
力的合成可以看作向量加法的平行四边形法则的物理模型
o
(二)新课探究
(1) 同向
(2)反向
A
B
C
A
B
C
(二)新课探究
结论:任意向量的加法满足交换律
(二)新课探究
结论:任意向量的加法也满足结合律
(二)新课探究
例1.如图,已知向量 ,求作向量 。
则
三角形法则
在平面内任取一点O,
作 , ,
作法1:
(三)典例分析
例1.如图,已知向量 ,求作向量 。
作法2:在平面内任取一点O,
作 , ,
连结OC,则
平行四边形法则
以 为邻边作 OACB ,
(三)典例分析
(三)典例分析
例2,轮船从A港沿北偏东60°方向行驶了40 n maile到达B处,再由B处沿正北方向行驶40 n mile到达C处.求此时轮船与A港的相对位置.
B
C
A
东
北
30°
解:
(三)典例分析
B
C
A
东
北
D
30°
解:
B过作垂线BD,垂足为D
1.化简
2.根据图示填空
A
B
D
E
C
(四)巩固练习
1.向量加法的三角形法则
(要点:两向量首尾连接)
2.向量加法的平行四边形法则
(要点:同一起点,对角线为和向量)
3.向量加法满足交换律及结合律
(五)课时小结
A
O
B
C
B
A
C
谢谢欣赏
§2.1从位移的合成到向量的加减法
北师大版(2017版)高中数学必修第二册第二章
第一课时 向量的加法
掌握向量加法的概念;能熟练运用三角形法则和平行四边形法则做几个向量的和向量;能准确表述向量加法的交换律和结合律,并能熟练运用它们进行向量计算.
学习目标:
学习重点难度
教学重点: 向量加法的概念和向量加法的法则及运算律.
教学难点: 向量加法的运算.
(一)创设情境
问题1:小明从A到B,再从B按原方向到C,
则两次的位移和:
问题2:若上题改为从A到B,再从B按反方向到C,
则两次的位移和:
问题3:某车从A到B,再从B改变方向到C,
则两次的位移和:
A
B
C
A
A
B
B
C
C
a
b
A
C
B
(二)新课探究
问题1:任意给出两个向量 与 ,如何求
O
问题2:两种方法做出的结果一样吗
a
a
b
b
A
C
B
b
a
(二)新课探究
尾首相连,起点指向终点为和
同一起点,对角线为和
问题1:任意给出两个向量 与 ,如何求
位移的合成可以看作向量加法三角形法则的物理模型
(二)新课探究
C
A
B
A
B
C
力的合成可以看作向量加法的平行四边形法则的物理模型
o
(二)新课探究
(1) 同向
(2)反向
A
B
C
A
B
C
(二)新课探究
结论:任意向量的加法满足交换律
(二)新课探究
结论:任意向量的加法也满足结合律
(二)新课探究
例1.如图,已知向量 ,求作向量 。
则
三角形法则
在平面内任取一点O,
作 , ,
作法1:
(三)典例分析
例1.如图,已知向量 ,求作向量 。
作法2:在平面内任取一点O,
作 , ,
连结OC,则
平行四边形法则
以 为邻边作 OACB ,
(三)典例分析
(三)典例分析
例2,轮船从A港沿北偏东60°方向行驶了40 n maile到达B处,再由B处沿正北方向行驶40 n mile到达C处.求此时轮船与A港的相对位置.
B
C
A
东
北
30°
解:
(三)典例分析
B
C
A
东
北
D
30°
解:
B过作垂线BD,垂足为D
1.化简
2.根据图示填空
A
B
D
E
C
(四)巩固练习
1.向量加法的三角形法则
(要点:两向量首尾连接)
2.向量加法的平行四边形法则
(要点:同一起点,对角线为和向量)
3.向量加法满足交换律及结合律
(五)课时小结
A
O
B
C
B
A
C
谢谢欣赏
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
