2021-2022学年高一下学期数学人教A版(2019)必修第二册6.1平面向量的概念课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年高一下学期数学人教A版(2019)必修第二册6.1平面向量的概念课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-20 11:12:45 | ||
图片预览







文档简介
(共28张PPT)
第六章 平面向量及其应用
6.1平面向量的概念
人教A版(2019)必修第二册
2、请同学们回忆在物理中学习过哪些既有大小又有方向的量?
G
F
1.小船快速向东南方向航行
2.桌面承受物体的重力
3.浮力让物体浮起来
1、请同学们回忆物理里面,标量是什么 ?矢量是什么?
新课引入
力、位移、速度各有特性,但也有共同属性,请问共同属性是什么?
在现实生活中,一些量如长度、面积、质量、年龄等和刚才几个量一样吗?
只有大小,数学中称之为数量.
既有大小,又有方向.大家猜猜数学中称之为什么?
新课引入
物理 数学
标量 数量
矢量 ?
在现实生活中,我们接触过很多量,像力、位移、速度等这些物理量既有大小,又有方向.而比如一支笔、一棵树、一本书……,只有大小却没有方向,可以抽象出只有大小的数量“1”.类似地,我们可以对力、位移、速度等这些量进行抽象形成一种新的量,也就是向量.
数学中,我们把既有大小又有方向的量叫做向量(vector),而把只有大小没有方向的量称为数量.
探求新知
向量的两要素:方向、大小
数量只有大小,是一个代数量,可以进行代数运算、能比较大小;
向量具有大小和方向这双重要素,由于方向不能比较大小,故向量不能比较大小.
数量与向量的联系与区别
向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁.
探求新知
下列不是向量的是( )
① 质量; ② 速度; ③位移; ④温度;
⑤加速度; ⑥路程; ⑦ 密度;⑧功.
① ④ ⑥⑦ ⑧
【即时训练】
有人说:由于海平面以上的高度(海拔)用正数表示,海平面以下的高度用负数表示,所以海拔也是向量.
你同意吗?温度、角度是向量吗?为什么?
【解】海拔不是向量,它只有大小没有方向.
海拔的正负不表示方向,只表示在海平面的上方还是下方.
同理,温度和角度也不是向量,因为它们没有方向.
向量的几何表示
向量
探求新知
由于数量可以用实数表示,而实数与数轴上的点一一对应,所以数量可用数轴上的点表示,而且不同的点表示不同的数量. 那么,该如何表示向量呢?
数量 实数 数轴上的点
O
3
-2
大小
大小+方向
?
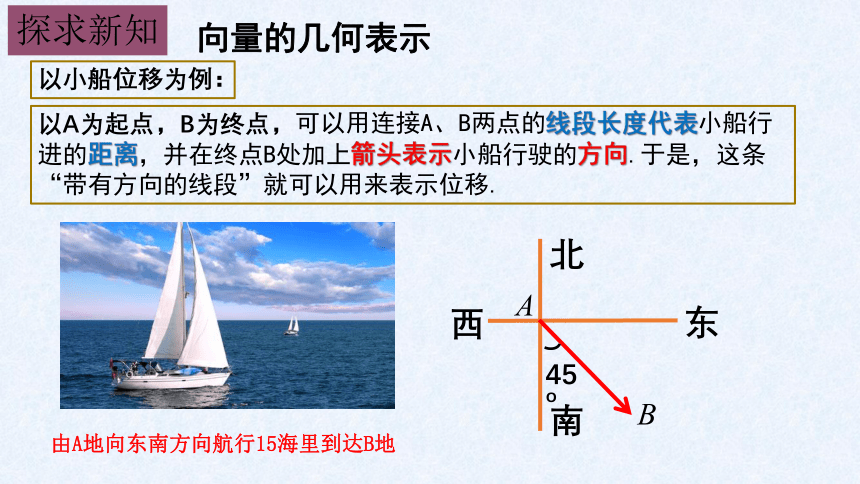
由A地向东南方向航行15海里到达B地
东
西
北
南
45o
向量的几何表示
探求新知
以小船位移为例:
以A为起点,B为终点,可以用连接A、B两点的线段长度代表小船行进的距离,并在终点B处加上箭头表示小船行驶的方向.于是,这条“带有方向的线段”就可以用来表示位移.
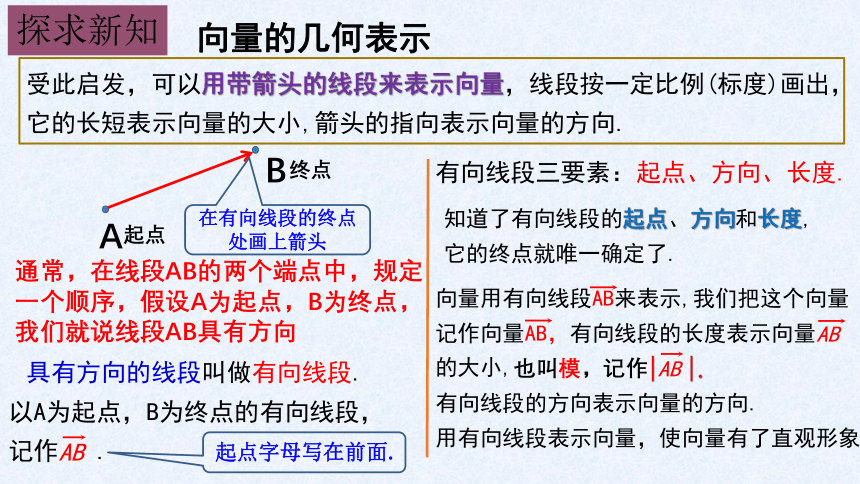
受此启发,可以用带箭头的线段来表示向量,线段按一定比例(标度)画出,它的长短表示向量的大小,箭头的指向表示向量的方向.
A
B
起点
终点
通常,在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向
向量的几何表示
探求新知
具有方向的线段叫做有向线段.
有向线段三要素:起点、方向、长度.
知道了有向线段的起点、方向和长度,
它的终点就唯一确定了.
以A为起点,B为终点的有向线段,
记作 .
AB
起点字母写在前面.
向量用有向线段AB来表示,我们把这个向量
记作向量AB,有向线段的长度表示向量
的大小,也叫模,记作
有向线段的方向表示向量的方向.
用有向线段表示向量,使向量有了直观形象.
AB
| |.
AB
在有向线段的终点处画上箭头
(1)有向线段就是向量,向量就是有向线段吗?
思考问题
探求新知
【1】从定义上看,它们都是既有大小又有方向的量,但有向线段不是向量.向量有大小和方向两个要素,而有向线段有起点、方向、长度三个要素,因此这是两个不同的量;
【2】在平面内,向量可以自由平移,而有向线段是固定的线段;
【3】向量可以用有向线段来表示,但是向量不是有向线段,也不能说有向线段是向量.
A(起点)
B(终点)
我们用有向线段表示向量,用有向线段的方向表示向量的方向,用有向线段的长度表示向量的大小,与起点的具体位置无关.
思考问题
(2)向量与有向线段的起点位置有关吗?
探求新知
向量可以用字母a,b,c,…表示
a
b
c
向量的字母表示法
在印刷时,用黑体小写字母a,b,c……表示向量,但手写时要写成带箭头的小写字母 ……
向量的字母表示法
思考:除了用有向线段表示向量,还有别的方法表示向量吗?
探求新知
向量的长度/模
向量 的大小称为向量 的长度(或称模),记作 .
长度为0的向量叫做零向量(zero vector),记作0,即|0|=0.
长度等于1个单位长度的向量,叫做单位向量(unit vector).若向量e为单位向量,则|e|=1.
向量的有关概念
特殊向量
注意:(1)零向量0的方向是任意的,所有的零向量0都相等.它与数字0不一样,数字0仅仅是一个只有大小的实数.
(2)单位向量不一定相等,易忽略向量的方向.
提醒:两个单位向量的模相等,但这两个单位向量不一定相等.
探求新知
D
【即时训练】
P
思考: 在平面上把所有单位向量的起点平移到同一点P,那么它们的终点的集合组成什么图形?
圆的半径是多少?
(1)温度含零上和零下温度,所以温度是向量( )
(2)向量的模是一个正实数( )
注意: 向量不能比较大小,向量的模可以比较大小
(3)若|a|>|b| ,则a > b ( )
例题2 如图所示,若每一个小格的边长均为1,指出图中各向量的长度,哪些是单位向量?
例题3 判断正误.
有意义
没有意义
探求新知
向量间的关系
思考:观察右图,你有什么发现?
记作 a ∥b ∥c
1.平行向量:方向相同或相反的非零向量叫做平行向量。
规定:0与任意向量平行。即对于任意向量a,都有0∥a
这就是说,任一组平行向量都可以平移到同一条直线上,因此,平行向量也叫做共线向量(collinear vectors).
a
b
c
O
A
B
C
l
探求新知
向量间的关系
如图,a, b, c是一组平行向量,任作一条与a所在直线平行的直线l,在l上任取一点O,则可在l上分别作出
注意:区别于平面几何中的直线平行。平行直线不包括重合的情况,而平行向量是可以重合的。
思考:如图所示两个向量 ,若两个向量大小相等,则它们是相同的向量吗?
是大小相等但方向相反的两个向量。这样的两个向量叫做相反向量。
同理可得,大小相等且方向相同的两个向量叫做相等向量。
注:向量是否相等(或相反)只与大小和方向有关,与起点、终点的位置无关. 任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关;同时方向相同且长度相等的有向线段表示同一个向量
与 长度相等,方向相反的向量叫 的相反向量.记为
探求新知
向量间的关系
a与b相等,记作 a =b .
规定:0 = 0
1.若a=b,则两向量在大小与方向上有何关系
几个容易混淆的知识
2.相等向量一定是平行向量吗?平行向量一定是相等向量吗?
3.如果 ,那么 吗
向量的平行不具有传递性,当 =0时,则不平行,只有当 ≠0才能得到平行。
向量相等 向量平行
探求新知
向量间的关系
若a=b,意味着|a|=|b|,且a与b的方向相同.
(1)若非零向量AB//CD ,那么AB//CD( )
(2)若a//b ,则a与b的方向一定相同或相反( )
(3)平行于同一个向量的两个向量平行( )
例题4 如图所示,找出其中平行的向量.
找出其中共线的向量.
例题5 判断正误.
注意零向量
找出与向量a平行的向量.
例题6 如图所示,已知四边形ABCD,则“四边形ABCD为平行四边形”是“ ”的什么条件?
A
B
C
D
例题 如右图,O是正六边形ABCDEF的中心.
(1)写出图中的共线向量;
(2)分别写出图中与 相等的向量.
1.思维辨析(对的打“√”,错的打“×”)
(1)两个有共同起点,且长度相等的向量,它们的终点相同.( )
(2)向量就是有向线段.( )
(3)零向量是最小的向量.( )
(4)单位向量都是同方向.( )
(5)长度为0的向量都是零向量.( )
(6)单位向量的长度都相等.( )
×
×
×
×
√
√
练习巩固
2.下列结论正确的是 _________(填写正确的序号).
(1)若a与b都是单位向量,则a=b.
(2)方向为南偏西60°的向量与北偏东60°的向量是共线向量.
(3)直角坐标平面上的x轴、y轴都是向量.
(4)若a与b是平行向量,则a=b.
(5)若用有向线段表示的向量 与 不相等,则点M与N不重合.
(6)海拔、温度、角度都不是向量.
(2)(5)(6)
练习巩固
3.如图,△ABC的三边均不相等,E、F、D分别是AC、AB、BC的中点.
(1)写出与 共线的向量;
(2)写出与 的模相等的向量;
(3)写出与 相等的向量.
练习巩固
D
B
应用知识
C
④⑥
应用知识
5.判断下列命题是否正确,若不正确,请简述理由.
①向量 与 是共线向量,则A、B、C、D 四点必在一直线上;
②单位向量都相等;
③零向量是没有方向的向量;
④共线的向量,若起点不同,则终点一定不同。
6. 下面几个命题中正确的个数是( )
(3)若|a|=|b|,则a = b
(2)若|a|=0,则a = 0
(1)若a = b,b = c,则a = c。
A.0 B. 1 C. 2 D. 3
B
应用知识
第六章 平面向量及其应用
6.1平面向量的概念
人教A版(2019)必修第二册
2、请同学们回忆在物理中学习过哪些既有大小又有方向的量?
G
F
1.小船快速向东南方向航行
2.桌面承受物体的重力
3.浮力让物体浮起来
1、请同学们回忆物理里面,标量是什么 ?矢量是什么?
新课引入
力、位移、速度各有特性,但也有共同属性,请问共同属性是什么?
在现实生活中,一些量如长度、面积、质量、年龄等和刚才几个量一样吗?
只有大小,数学中称之为数量.
既有大小,又有方向.大家猜猜数学中称之为什么?
新课引入
物理 数学
标量 数量
矢量 ?
在现实生活中,我们接触过很多量,像力、位移、速度等这些物理量既有大小,又有方向.而比如一支笔、一棵树、一本书……,只有大小却没有方向,可以抽象出只有大小的数量“1”.类似地,我们可以对力、位移、速度等这些量进行抽象形成一种新的量,也就是向量.
数学中,我们把既有大小又有方向的量叫做向量(vector),而把只有大小没有方向的量称为数量.
探求新知
向量的两要素:方向、大小
数量只有大小,是一个代数量,可以进行代数运算、能比较大小;
向量具有大小和方向这双重要素,由于方向不能比较大小,故向量不能比较大小.
数量与向量的联系与区别
向量既是代数研究对象,也是几何研究对象,是沟通几何与代数的桥梁.
探求新知
下列不是向量的是( )
① 质量; ② 速度; ③位移; ④温度;
⑤加速度; ⑥路程; ⑦ 密度;⑧功.
① ④ ⑥⑦ ⑧
【即时训练】
有人说:由于海平面以上的高度(海拔)用正数表示,海平面以下的高度用负数表示,所以海拔也是向量.
你同意吗?温度、角度是向量吗?为什么?
【解】海拔不是向量,它只有大小没有方向.
海拔的正负不表示方向,只表示在海平面的上方还是下方.
同理,温度和角度也不是向量,因为它们没有方向.
向量的几何表示
向量
探求新知
由于数量可以用实数表示,而实数与数轴上的点一一对应,所以数量可用数轴上的点表示,而且不同的点表示不同的数量. 那么,该如何表示向量呢?
数量 实数 数轴上的点
O
3
-2
大小
大小+方向
?
由A地向东南方向航行15海里到达B地
东
西
北
南
45o
向量的几何表示
探求新知
以小船位移为例:
以A为起点,B为终点,可以用连接A、B两点的线段长度代表小船行进的距离,并在终点B处加上箭头表示小船行驶的方向.于是,这条“带有方向的线段”就可以用来表示位移.
受此启发,可以用带箭头的线段来表示向量,线段按一定比例(标度)画出,它的长短表示向量的大小,箭头的指向表示向量的方向.
A
B
起点
终点
通常,在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向
向量的几何表示
探求新知
具有方向的线段叫做有向线段.
有向线段三要素:起点、方向、长度.
知道了有向线段的起点、方向和长度,
它的终点就唯一确定了.
以A为起点,B为终点的有向线段,
记作 .
AB
起点字母写在前面.
向量用有向线段AB来表示,我们把这个向量
记作向量AB,有向线段的长度表示向量
的大小,也叫模,记作
有向线段的方向表示向量的方向.
用有向线段表示向量,使向量有了直观形象.
AB
| |.
AB
在有向线段的终点处画上箭头
(1)有向线段就是向量,向量就是有向线段吗?
思考问题
探求新知
【1】从定义上看,它们都是既有大小又有方向的量,但有向线段不是向量.向量有大小和方向两个要素,而有向线段有起点、方向、长度三个要素,因此这是两个不同的量;
【2】在平面内,向量可以自由平移,而有向线段是固定的线段;
【3】向量可以用有向线段来表示,但是向量不是有向线段,也不能说有向线段是向量.
A(起点)
B(终点)
我们用有向线段表示向量,用有向线段的方向表示向量的方向,用有向线段的长度表示向量的大小,与起点的具体位置无关.
思考问题
(2)向量与有向线段的起点位置有关吗?
探求新知
向量可以用字母a,b,c,…表示
a
b
c
向量的字母表示法
在印刷时,用黑体小写字母a,b,c……表示向量,但手写时要写成带箭头的小写字母 ……
向量的字母表示法
思考:除了用有向线段表示向量,还有别的方法表示向量吗?
探求新知
向量的长度/模
向量 的大小称为向量 的长度(或称模),记作 .
长度为0的向量叫做零向量(zero vector),记作0,即|0|=0.
长度等于1个单位长度的向量,叫做单位向量(unit vector).若向量e为单位向量,则|e|=1.
向量的有关概念
特殊向量
注意:(1)零向量0的方向是任意的,所有的零向量0都相等.它与数字0不一样,数字0仅仅是一个只有大小的实数.
(2)单位向量不一定相等,易忽略向量的方向.
提醒:两个单位向量的模相等,但这两个单位向量不一定相等.
探求新知
D
【即时训练】
P
思考: 在平面上把所有单位向量的起点平移到同一点P,那么它们的终点的集合组成什么图形?
圆的半径是多少?
(1)温度含零上和零下温度,所以温度是向量( )
(2)向量的模是一个正实数( )
注意: 向量不能比较大小,向量的模可以比较大小
(3)若|a|>|b| ,则a > b ( )
例题2 如图所示,若每一个小格的边长均为1,指出图中各向量的长度,哪些是单位向量?
例题3 判断正误.
有意义
没有意义
探求新知
向量间的关系
思考:观察右图,你有什么发现?
记作 a ∥b ∥c
1.平行向量:方向相同或相反的非零向量叫做平行向量。
规定:0与任意向量平行。即对于任意向量a,都有0∥a
这就是说,任一组平行向量都可以平移到同一条直线上,因此,平行向量也叫做共线向量(collinear vectors).
a
b
c
O
A
B
C
l
探求新知
向量间的关系
如图,a, b, c是一组平行向量,任作一条与a所在直线平行的直线l,在l上任取一点O,则可在l上分别作出
注意:区别于平面几何中的直线平行。平行直线不包括重合的情况,而平行向量是可以重合的。
思考:如图所示两个向量 ,若两个向量大小相等,则它们是相同的向量吗?
是大小相等但方向相反的两个向量。这样的两个向量叫做相反向量。
同理可得,大小相等且方向相同的两个向量叫做相等向量。
注:向量是否相等(或相反)只与大小和方向有关,与起点、终点的位置无关. 任意两个相等的非零向量,都可用同一条有向线段表示,并且与有向线段的起点无关;同时方向相同且长度相等的有向线段表示同一个向量
与 长度相等,方向相反的向量叫 的相反向量.记为
探求新知
向量间的关系
a与b相等,记作 a =b .
规定:0 = 0
1.若a=b,则两向量在大小与方向上有何关系
几个容易混淆的知识
2.相等向量一定是平行向量吗?平行向量一定是相等向量吗?
3.如果 ,那么 吗
向量的平行不具有传递性,当 =0时,则不平行,只有当 ≠0才能得到平行。
向量相等 向量平行
探求新知
向量间的关系
若a=b,意味着|a|=|b|,且a与b的方向相同.
(1)若非零向量AB//CD ,那么AB//CD( )
(2)若a//b ,则a与b的方向一定相同或相反( )
(3)平行于同一个向量的两个向量平行( )
例题4 如图所示,找出其中平行的向量.
找出其中共线的向量.
例题5 判断正误.
注意零向量
找出与向量a平行的向量.
例题6 如图所示,已知四边形ABCD,则“四边形ABCD为平行四边形”是“ ”的什么条件?
A
B
C
D
例题 如右图,O是正六边形ABCDEF的中心.
(1)写出图中的共线向量;
(2)分别写出图中与 相等的向量.
1.思维辨析(对的打“√”,错的打“×”)
(1)两个有共同起点,且长度相等的向量,它们的终点相同.( )
(2)向量就是有向线段.( )
(3)零向量是最小的向量.( )
(4)单位向量都是同方向.( )
(5)长度为0的向量都是零向量.( )
(6)单位向量的长度都相等.( )
×
×
×
×
√
√
练习巩固
2.下列结论正确的是 _________(填写正确的序号).
(1)若a与b都是单位向量,则a=b.
(2)方向为南偏西60°的向量与北偏东60°的向量是共线向量.
(3)直角坐标平面上的x轴、y轴都是向量.
(4)若a与b是平行向量,则a=b.
(5)若用有向线段表示的向量 与 不相等,则点M与N不重合.
(6)海拔、温度、角度都不是向量.
(2)(5)(6)
练习巩固
3.如图,△ABC的三边均不相等,E、F、D分别是AC、AB、BC的中点.
(1)写出与 共线的向量;
(2)写出与 的模相等的向量;
(3)写出与 相等的向量.
练习巩固
D
B
应用知识
C
④⑥
应用知识
5.判断下列命题是否正确,若不正确,请简述理由.
①向量 与 是共线向量,则A、B、C、D 四点必在一直线上;
②单位向量都相等;
③零向量是没有方向的向量;
④共线的向量,若起点不同,则终点一定不同。
6. 下面几个命题中正确的个数是( )
(3)若|a|=|b|,则a = b
(2)若|a|=0,则a = 0
(1)若a = b,b = c,则a = c。
A.0 B. 1 C. 2 D. 3
B
应用知识
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
