北师大版八年级数学下册 第六章 平行四边形 章末检测(word版含解析)
文档属性
| 名称 | 北师大版八年级数学下册 第六章 平行四边形 章末检测(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 468.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 07:07:52 | ||
图片预览



文档简介
《第六章 平行四边形》章末检测
选择题
1.在平行四边形ABCD中,∠B=60°,那么下列各式中不成立的是( )
A.∠D=60°
B.∠A=120°
C.∠C+∠D=180°
D.∠C+∠A=180°
2.若一正多边形的内角和为540°,则该正多边形的每个外角的度数为( )
A.36°
B.72°
C.108°
D.360°
3.关于四边形ABCD有以下几个条件:①两组对边分别平行;②两组对边分别相等;③有两组角相等;④对角线AC和BD相等.其中可以判定四边形ABCD是平行四边形的有( )
A.1个
B.2个
C.3个
D.4个
4.(2020江苏常州溧阳期末)如图,平行四边形ABCD的对角线交于点O,且AB=8,△OCD的周长为20,则平行四边形ABCD的两条对角线长的和是( )
A.40
B.28
C.24
D.12
5.如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE= DF
B.BF= DE
C.AE=CF
D.∠1=∠2
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=50°,∠BAC=80°,则∠1的度数为( )
A.60°
B.50°
C.40°
D.25°
7.如图所示,M是ABCD的边AD上任意一点,若△CMB的面积为S,△CDM的面积为S1,△ABM的面积为S2,则下列说法中正确的是( )
A.
B.
C.
D.的关系无法确定
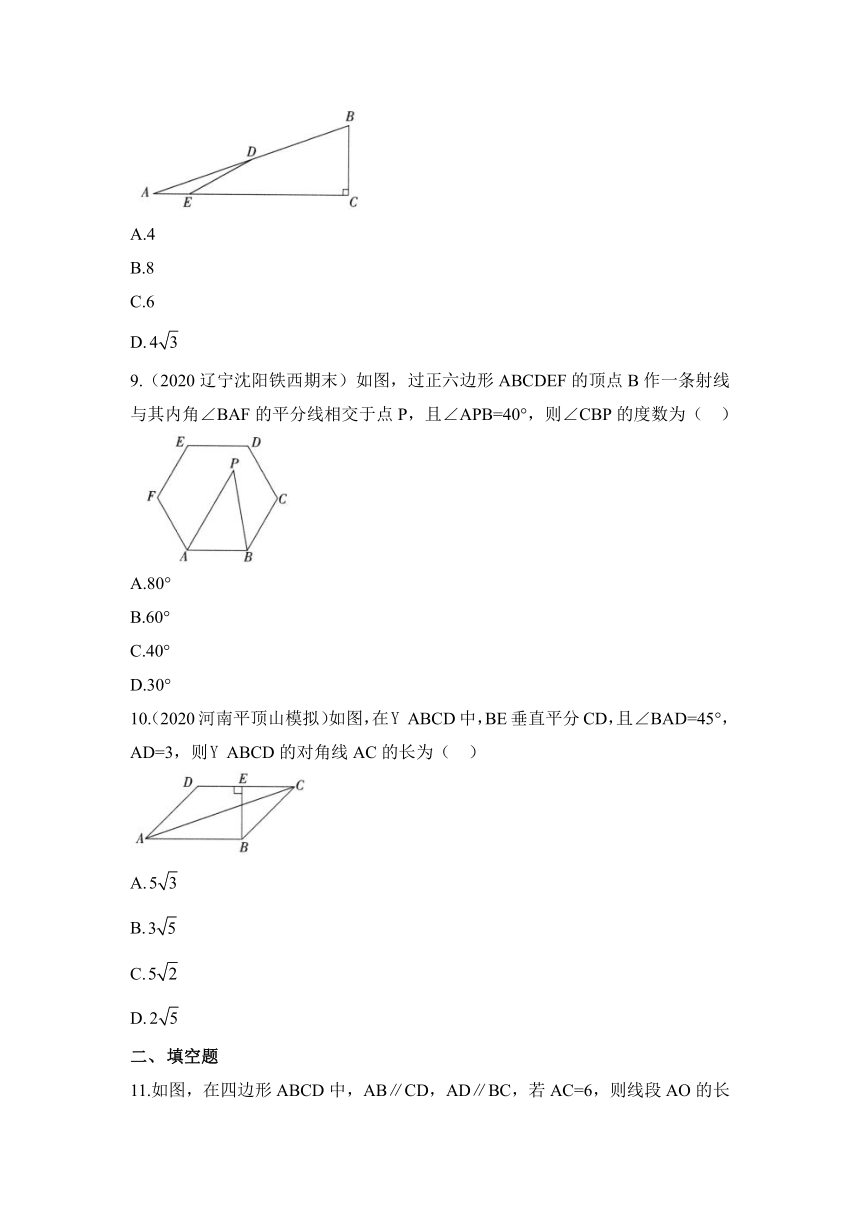
8.(2020独家原创试题)如图,△ABC中,∠C=90°,D是AB的中点,E在AC上,∠DEC=30°,DE=8,则BC的长为( )
A.4
B.8
C.6
D.
9.(2020辽宁沈阳铁西期末)如图,过正六边形ABCDEF的顶点B作一条射线与其内角∠BAF的平分线相交于点P,且∠APB=40°,则∠CBP的度数为( )
A.80°
B.60°
C.40°
D.30°
10.(2020河南平顶山模拟)如图,在ABCD中,BE垂直平分CD,且∠BAD=45°,AD=3,则ABCD的对角线AC的长为( )
A.
B.
C.
D.
填空题
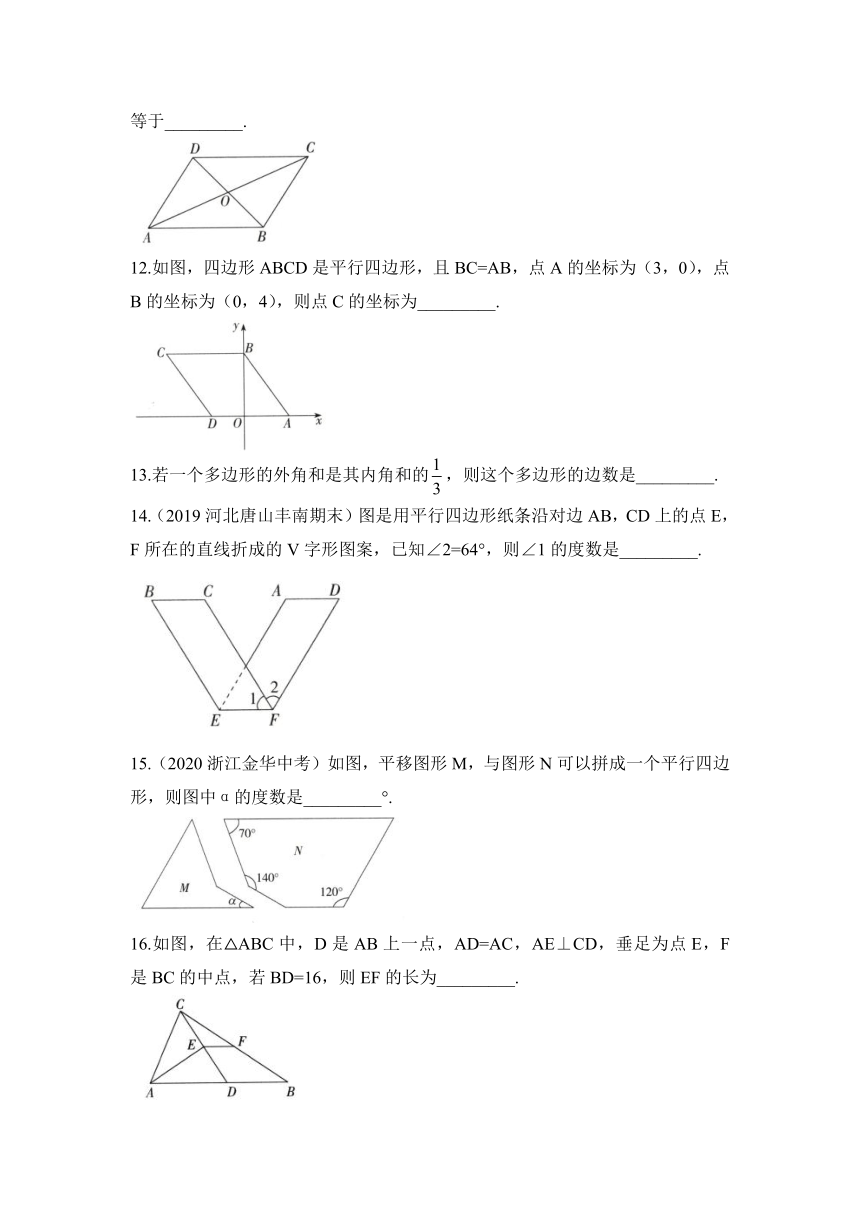
11.如图,在四边形ABCD中,AB∥CD,AD∥BC,若AC=6,则线段AO的长等于_________.
12.如图,四边形ABCD是平行四边形,且BC=AB,点A的坐标为(3,0),点B的坐标为(0,4),则点C的坐标为_________.
13.若一个多边形的外角和是其内角和的,则这个多边形的边数是_________.
14.(2019河北唐山丰南期末)图是用平行四边形纸条沿对边AB,CD上的点E,F所在的直线折成的V字形图案,已知∠2=64°,则∠1的度数是_________.
15.(2020浙江金华中考)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是_________°.
16.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为_________.
17.如图,在ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,若,则=_________.
18.(2020浙江宁波鄭州期中)如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积是_________.
解答题
19.(10分)一个正多边形的每一个内角都比其外角多100°,求该正多边形的边数.
20.(10分)如图,在□ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.求证:AE=BF.
21.(2018云南曲靖中考)(12分)如图,在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上的两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.
22.(2020山东淄博沂源一模)(14分)学习了《平行四边形》一章以后,小明根据学习平行四边形的经验,对平行四边形的判定问题进行了再次探究.
以下是小明的探究过程,请补充完整:
(1)在四边形ABCD中,对角线AC与BD相交于点O,若AB∥CD,补充下列条件中的__________,能判定四边形ABCD是平行四边形(写出你认为正确选项的序号即可);
A.BC=AD
B.AO=CO
(2)将(1)中的命题用文字语言表述如下:
①命题1:______________________________;
②画出图形,并写出命题1的已知、求证和证明;
(3)小明进一步探究发现:
若一个四边形ABCD的三个顶点A,B,C的位置如图所示,且这个四边形满足CD=AB,∠D=∠B,但四边形ABCD不是平行四边形,画出符合题意的四边形ABCD,进而小明发现:命题2:“一组对边相等,一组对角相等的四边形是平行四边形”是一个假命题.
参考答案
1.答案:D
解析:∵四边形ABCD是平行四边形,∴∠D=∠B=60°,故A成立;∵四边形ABCD是平行四边形,∴AD∥BC,∴∠A+∠B=180°,∴∠A=180°-∠B=120°,故B成立;∵四边形ABCD是平行四边形,∴AD∥BC,∴∠C+∠D=180°,故C成立;∵四边形ABCD是平行四边形,∴∠C=∠A=120°,故D不成立,故选D.
2.答案:B
解析:设这个正多边形的边数为n,则(n-2)·180°=540°,∴n=5,∴该正多边形的每个外角的度数为360°÷5=72°.故选B.
3.答案:B
解析:①是平行四边形的定义,②是平行四边形的判定定理.
4.答案:C
解析:∵四边形ABCD是平行四边形,
∴CD=AB=8,BD=2DO,AC=2OC,
∵△OCD的周长为20,
∴OD+OC=20-8=12,
∴平行四边形ABCD的两条对角线长的和=BD+AC=2(DO+OC)=24.故选C.
5.答案:C
解析:在ABCD中,AB∥CD,∴∠ABE=∠CDF.
添加AE=CF时,由“SSA”不能判定全等.
6.答案:B
解析:在△ABC中,∠ABC=50°,∠BAC=80°,
∴∠ACB=180°-50°-80°=50°.
∵四边形ABCD是平行四边形,∴OB=OD.
又∵E是CD的中点,∴OE是△BCD的中位线,
∴OE∥BC,∴∠1=∠ACB=50°.
7.答案:B
解析:过M作ME⊥BC于点E.∵四边形ABCD是平行四边形,∴AD=BC.∵△CMB的面积,△CDM的面积,△ABM的面积,∴S,S1,S2的关系是S=S1+S2,故选B.
8.答案:B
解析:取AC的中点F,连接DF,
∵D是AB的中点,∴DF∥BC,且DF=BC,
∵∠C=90°,∴∠DFE=∠C=90°,∵∠DEC=30°,∴DF=DE=4,∴BC=2DF=8.
9.答案:C
解析:∵多边形 ABCDEF是正六边形,
∴∠FAB=∠ABC=,
∵AP平分∠FAB,∴∠PAB=∠FAB=60°,
∵∠APB=40°,
∴∠ABP=180°-∠PAB-∠APB=80°,
∴∠CBP=∠ABC-∠ABP=40°.
故选C.
10.答案:B
解析:如图所示,连接BD,交AC于点O.
在ABCD中,BC=AD=3,∠BCD=∠BAD=45°,OB=OD,OA=OC.
∵BE垂直平分CD,∴BD=BC=3,
∴∠BDC=∠BCD=45°,∴∠CBD=90°,
∵BD=3,∴,
∴,
∴AC=2OC=.故选B.
11.答案:3
解析:∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∴OA=AC=3.
12.答案:(-5,4)
解析:∵点A的坐标为(3,0),点B的坐标为(0,4),∴OA=3,OB=4,∴,∴BC=AB=5,∵BC∥AD,点C在第二象限,∴点C的坐标为(-5,4).
13.答案:8
解析:∵一个多边形的外角和是其内角和的,多边形的外角和为360°,∴该多边形的内角和为360°×3=1080°.设这个多边形的边数为n,则(n-2)·180°=1080°,解得n=8,即这个多边形的边数是8.
14.答案:58°
解析:如图,根据题意可得∠3=∠1,
∵∠1+∠2+∠3=180°,∠2=64°,
∴∠1=(180°-64°)÷2=58°.
故答案为58°.
15.答案:30
解析:如图,∵四边形ABCD是平行四边形,
∴∠D+∠C=180°,
∴=180°-(540°-70°-140°-180°)=30°,
故答案为30.
16.答案:8
解析:∵AD=AC,AE⊥CD,∴CE=DE,又∵F是BC的中点,
∴EF是△BCD的中位线,∴EF=BD=8.
17.答案:18
解析:∵BF=2AF,
∴,
∴.
∵AE=2EC,∴,
∴.
∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,又∵AC=CA,
∴△ABC≌△CDA,∴
18.答案:8
解析:如图,连接EC,过A作AM∥BC交FE的延长线于M,
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE的DE边上的高和△CDE的DE边上的高相同,
∴△BDE的面积和△CDE的面积相等,
又△ADE的面积和△AME的面积相等,△DCE的面积和△FEC的面积相等
∴阴影部分的面积等于平行四边形ACFM的面积的一半,是(hCF为平行四边形ACFM的CF边上的高),
∵△ABC的面积是24,BC=3CF,
∴(hBC为△ABC的BC边上的高),
∴CF·hCF=16,
∴阴影部分的面积是×16=8,
故答案为8.
19.答案:见解析
解析:设该正多边形的每一个外角的度数为x,则每一个内角的度数为180°-x,
∴180°-x-x=100°,解得x=40°,
即该正多边形的每一个外角为40°,
∴这个正多边形的边数为360°÷40°=9.
20.答案:见解析
解析:证明:∵CF∥BD且CF=DE,
∴四边形CDEF是平行四边形,
∴CD∥EF,CD=EF.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴AB∥EF,AB=EF,
∴四边形ABFE是平行四边形,
∴AE= BF.
21.答案:见解析
解析:(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,∴∠AFN=∠CEM,
又∵FN=EM,AF=CE,∴△AFN≌△CEM(SAS).
(2)∵△AFN≌△CEM,∴∠NAF=∠MCE,
∵∠CMF=∠CEM+∠MCE,∴107°=72°+∠MCE,
∴∠MCE=35°,∴∠NAF=35°.
22.答案:见解析
解析:(1)B.
(2)①一组对边平行,一条对角线平分另一条对角线的四边形是平行四边形.
②已知:如图,在四边形ABCD中,AB∥CD,对角线AC与BD交于点O,AO=CO.
求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠ABO=∠CDO,∠BAO=∠DCO,
又∵AO=CO,∴△AOB≌△COD,∴AB=CD,
又∵AB∥CD,∴四边形ABCD是平行四边形.
(3)如图所示,四边形ABCD满足CD=AB,∠D=∠B,但四边形ABCD不是平行四边形.
选择题
1.在平行四边形ABCD中,∠B=60°,那么下列各式中不成立的是( )
A.∠D=60°
B.∠A=120°
C.∠C+∠D=180°
D.∠C+∠A=180°
2.若一正多边形的内角和为540°,则该正多边形的每个外角的度数为( )
A.36°
B.72°
C.108°
D.360°
3.关于四边形ABCD有以下几个条件:①两组对边分别平行;②两组对边分别相等;③有两组角相等;④对角线AC和BD相等.其中可以判定四边形ABCD是平行四边形的有( )
A.1个
B.2个
C.3个
D.4个
4.(2020江苏常州溧阳期末)如图,平行四边形ABCD的对角线交于点O,且AB=8,△OCD的周长为20,则平行四边形ABCD的两条对角线长的和是( )
A.40
B.28
C.24
D.12
5.如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
A.BE= DF
B.BF= DE
C.AE=CF
D.∠1=∠2
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,E是边CD的中点,连接OE.若∠ABC=50°,∠BAC=80°,则∠1的度数为( )
A.60°
B.50°
C.40°
D.25°
7.如图所示,M是ABCD的边AD上任意一点,若△CMB的面积为S,△CDM的面积为S1,△ABM的面积为S2,则下列说法中正确的是( )
A.
B.
C.
D.的关系无法确定
8.(2020独家原创试题)如图,△ABC中,∠C=90°,D是AB的中点,E在AC上,∠DEC=30°,DE=8,则BC的长为( )
A.4
B.8
C.6
D.
9.(2020辽宁沈阳铁西期末)如图,过正六边形ABCDEF的顶点B作一条射线与其内角∠BAF的平分线相交于点P,且∠APB=40°,则∠CBP的度数为( )
A.80°
B.60°
C.40°
D.30°
10.(2020河南平顶山模拟)如图,在ABCD中,BE垂直平分CD,且∠BAD=45°,AD=3,则ABCD的对角线AC的长为( )
A.
B.
C.
D.
填空题
11.如图,在四边形ABCD中,AB∥CD,AD∥BC,若AC=6,则线段AO的长等于_________.
12.如图,四边形ABCD是平行四边形,且BC=AB,点A的坐标为(3,0),点B的坐标为(0,4),则点C的坐标为_________.
13.若一个多边形的外角和是其内角和的,则这个多边形的边数是_________.
14.(2019河北唐山丰南期末)图是用平行四边形纸条沿对边AB,CD上的点E,F所在的直线折成的V字形图案,已知∠2=64°,则∠1的度数是_________.
15.(2020浙江金华中考)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是_________°.
16.如图,在△ABC中,D是AB上一点,AD=AC,AE⊥CD,垂足为点E,F是BC的中点,若BD=16,则EF的长为_________.
17.如图,在ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,若,则=_________.
18.(2020浙江宁波鄭州期中)如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积是_________.
解答题
19.(10分)一个正多边形的每一个内角都比其外角多100°,求该正多边形的边数.
20.(10分)如图,在□ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.求证:AE=BF.
21.(2018云南曲靖中考)(12分)如图,在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上的两点,且EM=FN,连接AN,CM.
(1)求证:△AFN≌△CEM;
(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.
22.(2020山东淄博沂源一模)(14分)学习了《平行四边形》一章以后,小明根据学习平行四边形的经验,对平行四边形的判定问题进行了再次探究.
以下是小明的探究过程,请补充完整:
(1)在四边形ABCD中,对角线AC与BD相交于点O,若AB∥CD,补充下列条件中的__________,能判定四边形ABCD是平行四边形(写出你认为正确选项的序号即可);
A.BC=AD
B.AO=CO
(2)将(1)中的命题用文字语言表述如下:
①命题1:______________________________;
②画出图形,并写出命题1的已知、求证和证明;
(3)小明进一步探究发现:
若一个四边形ABCD的三个顶点A,B,C的位置如图所示,且这个四边形满足CD=AB,∠D=∠B,但四边形ABCD不是平行四边形,画出符合题意的四边形ABCD,进而小明发现:命题2:“一组对边相等,一组对角相等的四边形是平行四边形”是一个假命题.
参考答案
1.答案:D
解析:∵四边形ABCD是平行四边形,∴∠D=∠B=60°,故A成立;∵四边形ABCD是平行四边形,∴AD∥BC,∴∠A+∠B=180°,∴∠A=180°-∠B=120°,故B成立;∵四边形ABCD是平行四边形,∴AD∥BC,∴∠C+∠D=180°,故C成立;∵四边形ABCD是平行四边形,∴∠C=∠A=120°,故D不成立,故选D.
2.答案:B
解析:设这个正多边形的边数为n,则(n-2)·180°=540°,∴n=5,∴该正多边形的每个外角的度数为360°÷5=72°.故选B.
3.答案:B
解析:①是平行四边形的定义,②是平行四边形的判定定理.
4.答案:C
解析:∵四边形ABCD是平行四边形,
∴CD=AB=8,BD=2DO,AC=2OC,
∵△OCD的周长为20,
∴OD+OC=20-8=12,
∴平行四边形ABCD的两条对角线长的和=BD+AC=2(DO+OC)=24.故选C.
5.答案:C
解析:在ABCD中,AB∥CD,∴∠ABE=∠CDF.
添加AE=CF时,由“SSA”不能判定全等.
6.答案:B
解析:在△ABC中,∠ABC=50°,∠BAC=80°,
∴∠ACB=180°-50°-80°=50°.
∵四边形ABCD是平行四边形,∴OB=OD.
又∵E是CD的中点,∴OE是△BCD的中位线,
∴OE∥BC,∴∠1=∠ACB=50°.
7.答案:B
解析:过M作ME⊥BC于点E.∵四边形ABCD是平行四边形,∴AD=BC.∵△CMB的面积,△CDM的面积,△ABM的面积,∴S,S1,S2的关系是S=S1+S2,故选B.
8.答案:B
解析:取AC的中点F,连接DF,
∵D是AB的中点,∴DF∥BC,且DF=BC,
∵∠C=90°,∴∠DFE=∠C=90°,∵∠DEC=30°,∴DF=DE=4,∴BC=2DF=8.
9.答案:C
解析:∵多边形 ABCDEF是正六边形,
∴∠FAB=∠ABC=,
∵AP平分∠FAB,∴∠PAB=∠FAB=60°,
∵∠APB=40°,
∴∠ABP=180°-∠PAB-∠APB=80°,
∴∠CBP=∠ABC-∠ABP=40°.
故选C.
10.答案:B
解析:如图所示,连接BD,交AC于点O.
在ABCD中,BC=AD=3,∠BCD=∠BAD=45°,OB=OD,OA=OC.
∵BE垂直平分CD,∴BD=BC=3,
∴∠BDC=∠BCD=45°,∴∠CBD=90°,
∵BD=3,∴,
∴,
∴AC=2OC=.故选B.
11.答案:3
解析:∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∴OA=AC=3.
12.答案:(-5,4)
解析:∵点A的坐标为(3,0),点B的坐标为(0,4),∴OA=3,OB=4,∴,∴BC=AB=5,∵BC∥AD,点C在第二象限,∴点C的坐标为(-5,4).
13.答案:8
解析:∵一个多边形的外角和是其内角和的,多边形的外角和为360°,∴该多边形的内角和为360°×3=1080°.设这个多边形的边数为n,则(n-2)·180°=1080°,解得n=8,即这个多边形的边数是8.
14.答案:58°
解析:如图,根据题意可得∠3=∠1,
∵∠1+∠2+∠3=180°,∠2=64°,
∴∠1=(180°-64°)÷2=58°.
故答案为58°.
15.答案:30
解析:如图,∵四边形ABCD是平行四边形,
∴∠D+∠C=180°,
∴=180°-(540°-70°-140°-180°)=30°,
故答案为30.
16.答案:8
解析:∵AD=AC,AE⊥CD,∴CE=DE,又∵F是BC的中点,
∴EF是△BCD的中位线,∴EF=BD=8.
17.答案:18
解析:∵BF=2AF,
∴,
∴.
∵AE=2EC,∴,
∴.
∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,又∵AC=CA,
∴△ABC≌△CDA,∴
18.答案:8
解析:如图,连接EC,过A作AM∥BC交FE的延长线于M,
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE的DE边上的高和△CDE的DE边上的高相同,
∴△BDE的面积和△CDE的面积相等,
又△ADE的面积和△AME的面积相等,△DCE的面积和△FEC的面积相等
∴阴影部分的面积等于平行四边形ACFM的面积的一半,是(hCF为平行四边形ACFM的CF边上的高),
∵△ABC的面积是24,BC=3CF,
∴(hBC为△ABC的BC边上的高),
∴CF·hCF=16,
∴阴影部分的面积是×16=8,
故答案为8.
19.答案:见解析
解析:设该正多边形的每一个外角的度数为x,则每一个内角的度数为180°-x,
∴180°-x-x=100°,解得x=40°,
即该正多边形的每一个外角为40°,
∴这个正多边形的边数为360°÷40°=9.
20.答案:见解析
解析:证明:∵CF∥BD且CF=DE,
∴四边形CDEF是平行四边形,
∴CD∥EF,CD=EF.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴AB∥EF,AB=EF,
∴四边形ABFE是平行四边形,
∴AE= BF.
21.答案:见解析
解析:(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB,∴∠AFN=∠CEM,
又∵FN=EM,AF=CE,∴△AFN≌△CEM(SAS).
(2)∵△AFN≌△CEM,∴∠NAF=∠MCE,
∵∠CMF=∠CEM+∠MCE,∴107°=72°+∠MCE,
∴∠MCE=35°,∴∠NAF=35°.
22.答案:见解析
解析:(1)B.
(2)①一组对边平行,一条对角线平分另一条对角线的四边形是平行四边形.
②已知:如图,在四边形ABCD中,AB∥CD,对角线AC与BD交于点O,AO=CO.
求证:四边形ABCD是平行四边形.
证明:∵AB∥CD,
∴∠ABO=∠CDO,∠BAO=∠DCO,
又∵AO=CO,∴△AOB≌△COD,∴AB=CD,
又∵AB∥CD,∴四边形ABCD是平行四边形.
(3)如图所示,四边形ABCD满足CD=AB,∠D=∠B,但四边形ABCD不是平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
