北师大版八年级数学下册 第六章 平行四边形 单元测试(word版含答案)
文档属性
| 名称 | 北师大版八年级数学下册 第六章 平行四边形 单元测试(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 361.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 07:17:15 | ||
图片预览

文档简介
单元测试(六) 平行四边形
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个正确的.
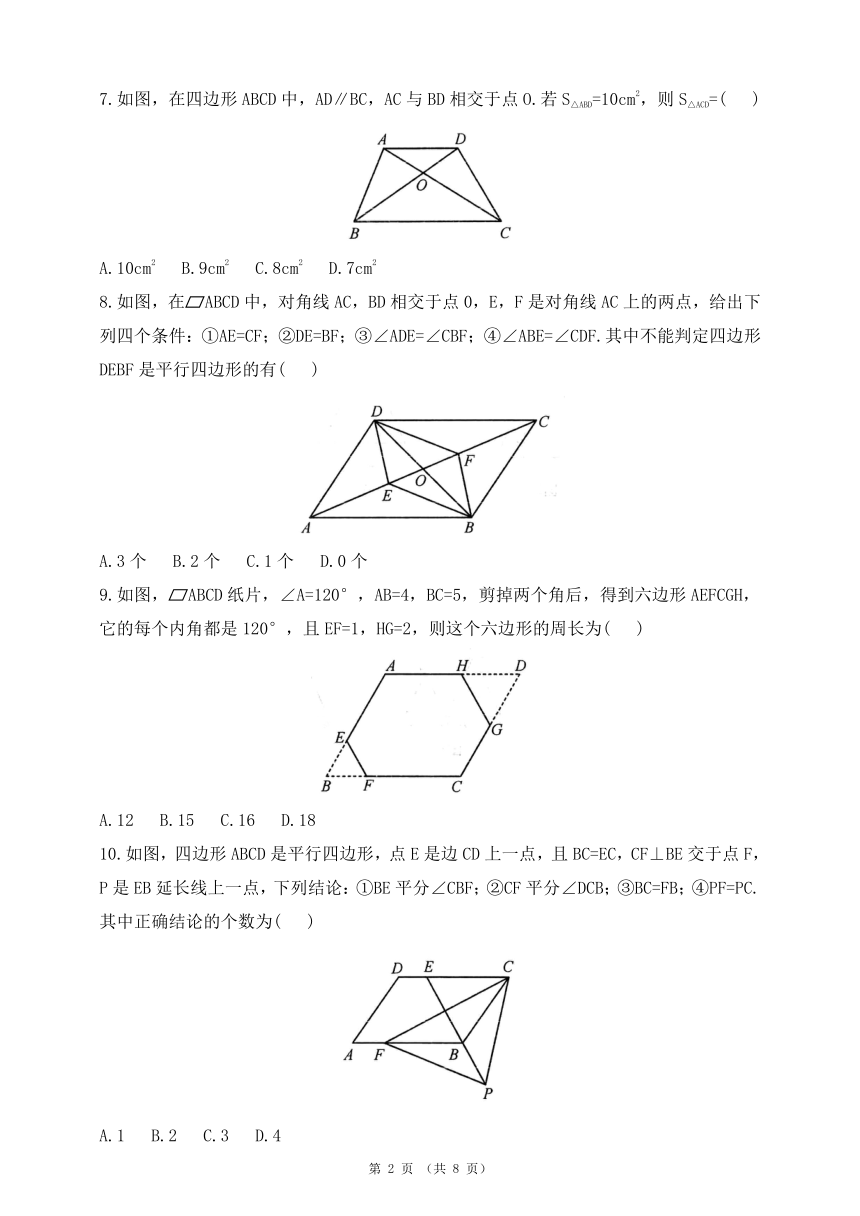
1.如图,在ABCD中,AB=3,AD=2,则CD=( )
A.3 B.2 C.1 D.5
2.若一个多边形的每个外角都等于36°,则它的内角和是( )
A.1080° B.1440° C.1800° D.2160°
3.下列性质中,平行四边形不一定具备的是( )
A.对边相等 B.对角相等 C.对角线互相平分 D.是轴对称图形
4.如图,在ABCD中,F是AD上的一点,CF=CD.若∠B=72°,则∠AFC的度数是( )
A.144° B.108° C.102° D.78°
5.如图所示,在平面直角坐标系中,原点0恰好是OABCD对角线的交点.若点A坐标为(2,3),则点C坐标为( )
A.(-3,-2) B.(-2,3) C.(-2,-3) D.(2,-3)
6.如图,已知四边形ABCD的面积为8cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A.4cm2 B.3cm2 C.2cm2 D.1cm2
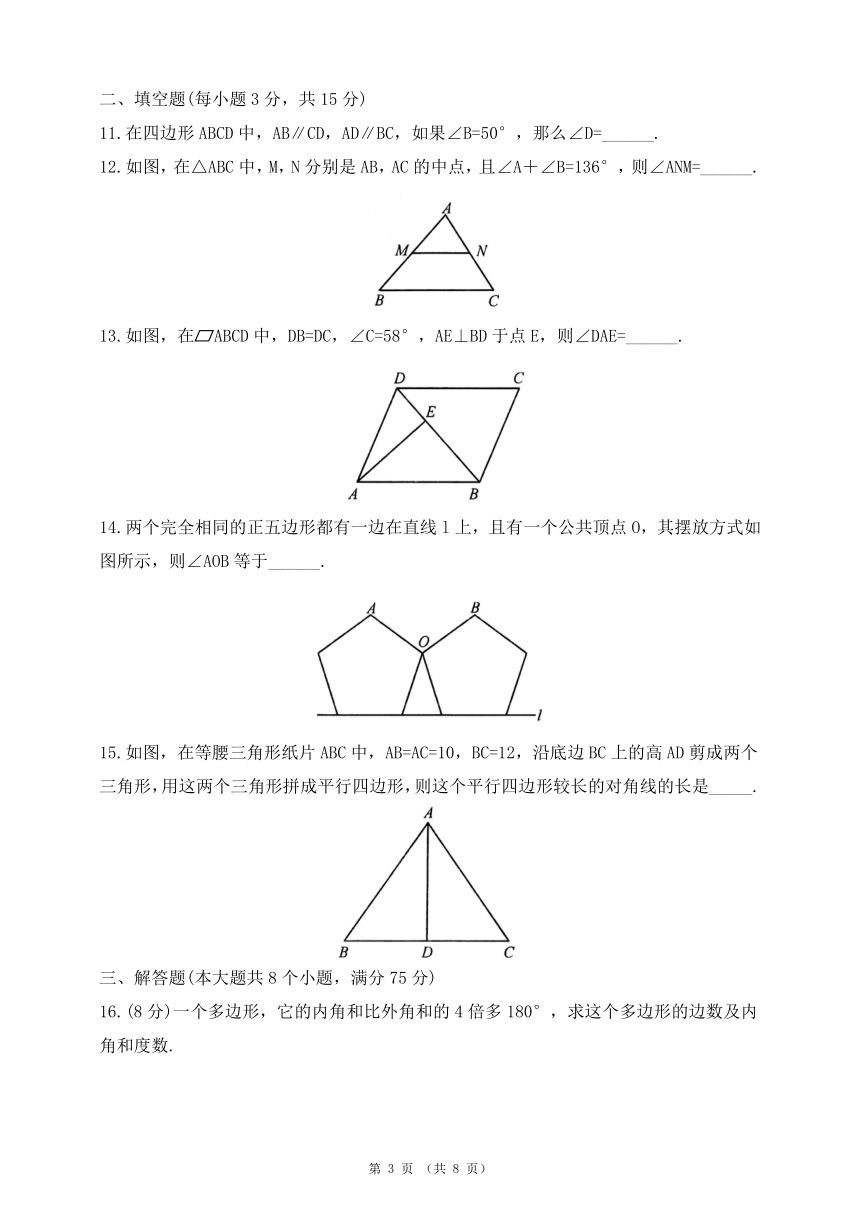
7.如图,在四边形ABCD中,AD∥BC,AC与BD相交于点O.若S△ABD=10cm2,则S△ACD=( )
A.10cm2 B.9cm2 C.8cm2 D.7cm2
8.如图,在ABCD中,对角线AC,BD相交于点0,E,F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.3个 B.2个 C.1个 D.0个
9.如图,ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
A.12 B.15 C.16 D.18
10.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共15分)
11.在四边形ABCD中,AB∥CD,AD∥BC,如果∠B=50°,那么∠D=______.
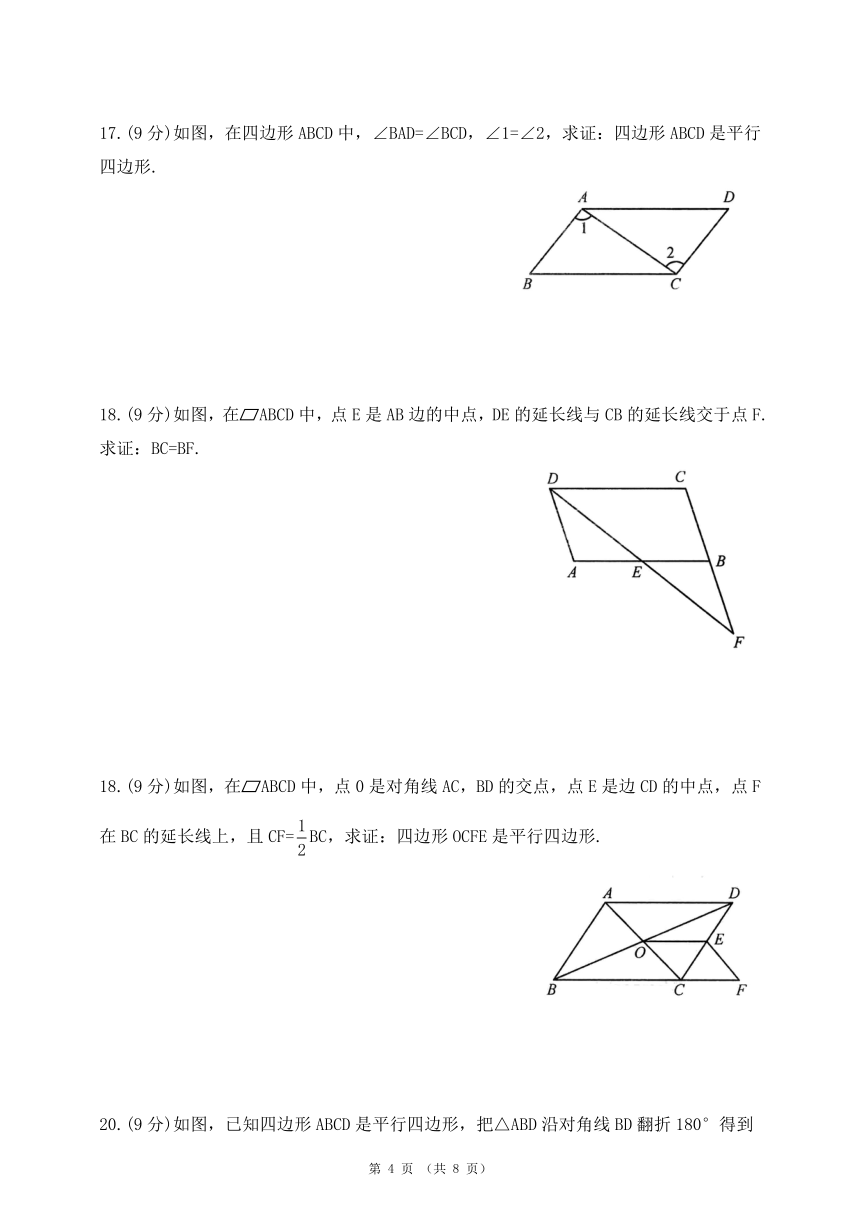
12.如图,在△ABC中,M,N分别是AB,AC的中点,且∠A+∠B=136°,则∠ANM=______.
13.如图,在ABCD中,DB=DC,∠C=58°,AE⊥BD于点E,则∠DAE=______.
14.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于______.
15.如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是_____.
三、解答题(本大题共8个小题,满分75分)
16.(8分)一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.
17.(9分)如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形.
18.(9分)如图,在ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.求证:BC=BF.
18.(9分)如图,在ABCD中,点0是对角线AC,BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=BC,求证:四边形OCFE是平行四边形.
20.(9分)如图,已知四边形ABCD是平行四边形,把△ABD沿对角线BD翻折180°得到△A’BD.
(1)利用尺规作出△A’BD(要求保留作图痕迹,不写作法);
(2)设DA’与BC交于点E,求证:△BA’E≌△DCE.
21.(10分)如图,在ABCD中,点E,F分别在CD,BC延长线上,AE∥BD,EF⊥BF.
(1)求证:四边形ABDE是平行四边形;
(2)若∠ABC=60°,CF=,求AB的长.
22.(10分)如图1,在ABCD中,点O是对角线AC的中点,EF过点0,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
23.(11分)在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
(1)如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系是PD+PE+PF=AB;当点P在△ABC内时,先在图2中作出相应的图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论;
(2)如图3,当点P在△ABC外时,先在图3中作出相应的图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)
参考答案
1.A 2.B 3.D 4.B 5.C 6.C 7.A 8.C 9.B 10.D
11.50°
12.44°
13.32°
14.108°
15.10或2或416.这个多边形的边数是11,内角和是1620°.
17.证明:∵∠BAD=∠BCD,∠1=∠2,∴∠CAD=∠ACB,∴AD∥BC.∵∠1=∠2,AC=CA. ∴△ACD≌△CAB(ASA).∴AD=BC.∴四边形ABCD是平行四边形.
18.证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴AD∥CF. ∴∠ADE=∠F.∵点E是AB边的中点,∴AE=BE.
在△ADE和△BFE中,,∴△ADE≌△BFE(AAS).∴AD=BF.∴BC=BF.
19.证明:∵四边形ABCD是平行四边形,∴点O是BD的中点.又∵点E是边CD的中点,∴0E是△BCD的中位线.∴0E∥BC,且0E=BC.又∵CF=BC,∴0E=CF.又∵OE∥CF,∴四边形OCFE是平行四边形.
20.(1)图略.(2)证明:∵四边形ABCD是平行四边形,∴AB=CD,∠BAD=∠C.
由折叠的性质可得∠BA’D=∠BAD,A’B=AB,∴∠BA’D=∠C,,A’B=CD.在△BA’E和△DCE中,,∴△BA’E≌△DCE(△AS).
21.(1)证明:在ABCD中,AB∥DC,∵点E在CD的延长线上,∴AB∥DE.又∵AE∥BD,∴四边形ABDE是平行四边形.
(2)AB=.
22.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC.∴∠EAO=∠FCO. ∵0是AC中点,∴OA=OC.在△OAE和△OCF中,,∴△OAE≌△OCF(ASA).∴0E=OF.同理OG=OH.∴四边形EGFH是平行四边形.
(2)GBCH,ABFE,EFCD,EGFH.
23.(1)图略,PD+PE+PF=AB.证明:∵PE∥AC.PF∥AB,∴四边形PEAF是平行四边形. ∴PE=AF.∵FD∥AB,∴∠B=∠FDC. ∵AB=AC,∴∠B=∠C.∴∠FDC=∠C.∴FD=FC,即PF+PD=FC.∴PE+PF+PD=AF+FC=AC=AB.
(2)图略,PE+PF-PD=AB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第 1 页 (共 8 页)
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个正确的.
1.如图,在ABCD中,AB=3,AD=2,则CD=( )
A.3 B.2 C.1 D.5
2.若一个多边形的每个外角都等于36°,则它的内角和是( )
A.1080° B.1440° C.1800° D.2160°
3.下列性质中,平行四边形不一定具备的是( )
A.对边相等 B.对角相等 C.对角线互相平分 D.是轴对称图形
4.如图,在ABCD中,F是AD上的一点,CF=CD.若∠B=72°,则∠AFC的度数是( )
A.144° B.108° C.102° D.78°
5.如图所示,在平面直角坐标系中,原点0恰好是OABCD对角线的交点.若点A坐标为(2,3),则点C坐标为( )
A.(-3,-2) B.(-2,3) C.(-2,-3) D.(2,-3)
6.如图,已知四边形ABCD的面积为8cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A.4cm2 B.3cm2 C.2cm2 D.1cm2
7.如图,在四边形ABCD中,AD∥BC,AC与BD相交于点O.若S△ABD=10cm2,则S△ACD=( )
A.10cm2 B.9cm2 C.8cm2 D.7cm2
8.如图,在ABCD中,对角线AC,BD相交于点0,E,F是对角线AC上的两点,给出下列四个条件:①AE=CF;②DE=BF;③∠ADE=∠CBF;④∠ABE=∠CDF.其中不能判定四边形DEBF是平行四边形的有( )
A.3个 B.2个 C.1个 D.0个
9.如图,ABCD纸片,∠A=120°,AB=4,BC=5,剪掉两个角后,得到六边形AEFCGH,它的每个内角都是120°,且EF=1,HG=2,则这个六边形的周长为( )
A.12 B.15 C.16 D.18
10.如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
A.1 B.2 C.3 D.4
二、填空题(每小题3分,共15分)
11.在四边形ABCD中,AB∥CD,AD∥BC,如果∠B=50°,那么∠D=______.
12.如图,在△ABC中,M,N分别是AB,AC的中点,且∠A+∠B=136°,则∠ANM=______.
13.如图,在ABCD中,DB=DC,∠C=58°,AE⊥BD于点E,则∠DAE=______.
14.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,其摆放方式如图所示,则∠AOB等于______.
15.如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,沿底边BC上的高AD剪成两个三角形,用这两个三角形拼成平行四边形,则这个平行四边形较长的对角线的长是_____.
三、解答题(本大题共8个小题,满分75分)
16.(8分)一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.
17.(9分)如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形.
18.(9分)如图,在ABCD中,点E是AB边的中点,DE的延长线与CB的延长线交于点F.求证:BC=BF.
18.(9分)如图,在ABCD中,点0是对角线AC,BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=BC,求证:四边形OCFE是平行四边形.
20.(9分)如图,已知四边形ABCD是平行四边形,把△ABD沿对角线BD翻折180°得到△A’BD.
(1)利用尺规作出△A’BD(要求保留作图痕迹,不写作法);
(2)设DA’与BC交于点E,求证:△BA’E≌△DCE.
21.(10分)如图,在ABCD中,点E,F分别在CD,BC延长线上,AE∥BD,EF⊥BF.
(1)求证:四边形ABDE是平行四边形;
(2)若∠ABC=60°,CF=,求AB的长.
22.(10分)如图1,在ABCD中,点O是对角线AC的中点,EF过点0,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.
(1)求证:四边形EGFH是平行四边形;
(2)如图2,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图2中与四边形AGHD面积相等的所有平行四边形(四边形AGHD除外).
23.(11分)在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
(1)如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系是PD+PE+PF=AB;当点P在△ABC内时,先在图2中作出相应的图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论;
(2)如图3,当点P在△ABC外时,先在图3中作出相应的图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)
参考答案
1.A 2.B 3.D 4.B 5.C 6.C 7.A 8.C 9.B 10.D
11.50°
12.44°
13.32°
14.108°
15.10或2或416.这个多边形的边数是11,内角和是1620°.
17.证明:∵∠BAD=∠BCD,∠1=∠2,∴∠CAD=∠ACB,∴AD∥BC.∵∠1=∠2,AC=CA. ∴△ACD≌△CAB(ASA).∴AD=BC.∴四边形ABCD是平行四边形.
18.证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∴AD∥CF. ∴∠ADE=∠F.∵点E是AB边的中点,∴AE=BE.
在△ADE和△BFE中,,∴△ADE≌△BFE(AAS).∴AD=BF.∴BC=BF.
19.证明:∵四边形ABCD是平行四边形,∴点O是BD的中点.又∵点E是边CD的中点,∴0E是△BCD的中位线.∴0E∥BC,且0E=BC.又∵CF=BC,∴0E=CF.又∵OE∥CF,∴四边形OCFE是平行四边形.
20.(1)图略.(2)证明:∵四边形ABCD是平行四边形,∴AB=CD,∠BAD=∠C.
由折叠的性质可得∠BA’D=∠BAD,A’B=AB,∴∠BA’D=∠C,,A’B=CD.在△BA’E和△DCE中,,∴△BA’E≌△DCE(△AS).
21.(1)证明:在ABCD中,AB∥DC,∵点E在CD的延长线上,∴AB∥DE.又∵AE∥BD,∴四边形ABDE是平行四边形.
(2)AB=.
22.(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC.∴∠EAO=∠FCO. ∵0是AC中点,∴OA=OC.在△OAE和△OCF中,,∴△OAE≌△OCF(ASA).∴0E=OF.同理OG=OH.∴四边形EGFH是平行四边形.
(2)GBCH,ABFE,EFCD,EGFH.
23.(1)图略,PD+PE+PF=AB.证明:∵PE∥AC.PF∥AB,∴四边形PEAF是平行四边形. ∴PE=AF.∵FD∥AB,∴∠B=∠FDC. ∵AB=AC,∴∠B=∠C.∴∠FDC=∠C.∴FD=FC,即PF+PD=FC.∴PE+PF+PD=AF+FC=AC=AB.
(2)图略,PE+PF-PD=AB.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
第 1 页 (共 8 页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
