【解析】上海市松江区2013届高三上学期期末质量监控数学理试题
文档属性
| 名称 | 【解析】上海市松江区2013届高三上学期期末质量监控数学理试题 |  | |
| 格式 | zip | ||
| 文件大小 | 457.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-03 10:13:53 | ||
图片预览




文档简介
松江区2012学年度第一学期高三期末考试
数学(理科)试卷(一模)
(满分150分,完卷时间120分钟) 2013.1
一、填空题 (本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.已知集合,,若,则 ▲ .
【答案】4
【21世纪教育网解析】因为,所以或。若,则,,满足。若,则,,不满足,所以。
2.若行列式,则 ▲ .
【答案】2
【21世纪教育网解析】由得,即,所以。
3.若函数的图像与的图像关于直线对称,则= ▲ .
【答案】1
【21世纪教育网解析】因为函数的图像与的图像关于直线对称,所以由,即,所以,所以。
4.某林场有树苗30000棵,其中松树苗4000棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为 ▲ .
【答案】20
【21世纪教育网解析】设样本中松树苗的数量为,则有,解得。
5.已知数列的前项和,则 ▲ .
【答案】5
【21世纪教育网解析】因为,所以。
6.己知,,且,则 ▲ ..[21世纪教育网]
【答案】
【21世纪教育网解析】因为,所以,即,所以。
7.抛物线的焦点为椭圆 的右焦点,顶点在椭圆的中心,则抛物线方程为 ▲
【答案】
【21世纪教育网解析】由椭圆方程可知,所以,即,所以椭圆的右焦点为,因为抛物线的焦点为椭圆的右焦点,所以,所以。所以抛物线的方程为。
8.已知,则的最小值为 ▲ .
【答案】2
【21世纪教育网解析】由得且,即。所以,所以的最小值为2.
9.在△ABC中,角所对的边分别是,若,且,
则△ABC的面积等于 ▲ .
【答案】
【21世纪教育网解析】由得,所以,所以,所以。
10.若二项式展开式中项的系数是7,则= ▲ .
【答案】
【21世纪教育网解析】二项展开式的通项为,令得,,所以,所以的系数为,所以。所以。
11.给出四个函数:①,②,③,④,其中满足条件:对任意实数及任意正数,都有及的函数为 ▲ .(写出所有满足条件的函数的序号)
【答案】③
【21世纪教育网解析】由得,所以函数为奇函数。对任意实数及任意正数由可知,函数为增函数。①为奇函数,但在上不单调。②为偶函数。,③满足条件。④为奇函数,但在在上不单调。所以满足条件的函数的序号为③。
12.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为,再由乙猜想甲刚才想的数字,把乙猜的数字记为,且,若,则称甲乙“心有灵犀”.现找两个人玩这个游戏,得出他们“心有灵犀”的概率为 ▲ .
【答案】
【21世纪教育网解析】试验发生的所有事件是从0,1,2,3,4,5,6,7,8,9十个数中任取两个共有10×10种不同的结果,
则的情况有0,0;1,1;2,2;3,3;4,4;5,5;6,6;7,7;8,8;9,9;0,1;1,0;1,2;2,1;2,3;3,2;3,4;4,3;4,5;5,4;5,6;6,5;6,7;7,6;7,8;8,7;8,9;9,8共28种情况,
甲乙出现的结果共有10×10=100,
所以他们”心有灵犀”的概率为P==.
13.已知是定义在上的增函数,且的图像关于点对称.若实数满足不等式,则的取值范围是 ▲ .
【答案】
【21世纪教育网解析】因为函数的图像关于点对称,所以,由得,因为函数是定义在上的增函数,所以得,即,配方得,所以圆心为,半径为1,的几何意义为圆上动点到原点距离的平方的最值。圆心到原点的距离为,所以动点到原点的距离的范围是,所以,所以的取值范围是。
14.定义变换将平面内的点变换到平面内的点.
若曲线经变换后得到曲线,曲线经变换后得到曲线,依次类推,曲线经变换后得到曲线,当时,记曲线与、轴正半轴的交点为和.某同学研究后认为曲线具有如下性质:
①对任意的,曲线都关于原点对称;
②对任意的,曲线恒过点;
③对任意的,曲线均在矩形(含边界)的内部,其中的坐标为;
④记矩形的面积为,则
其中所有正确结论的序号是 ▲ .
【答案】③④
【21世纪教育网解析】设上一点,则该点是由变换来的,所以,即。①因为,所以不可能关于原点对称,所以①错误。②当,则,所以,所以②错误。③因为,所以曲线均在矩形(含边界)的内部,所以③正确。④因为,所以,所以,所以④正确,所以所有正确结论的序号是③④。
二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生必须在答题纸相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.21世纪教育网
15.过点且与直线平行的直线方程是
A. B.
C. D.
【答案】D
【21世纪教育网解析】设所求的平行直线方程为,因为直线过点,所以,即,所以所求直线方程为,选D.
16.对于原命题:“已知,若 ,则”,以及它的逆命题、否命题、逆否命题,在这4个命题中,真命题的个数为
A.0个 B.1个 C.2个 D.4个
【答案】C
【21世纪教育网解析】当时,不成立,所以原命题错误,即逆否命题错误。原命题的逆命题为“已知,若 ,则”,所以逆命题正确,即否命题也正确,所以这4个命题中,真命题的个数为2个,选C.
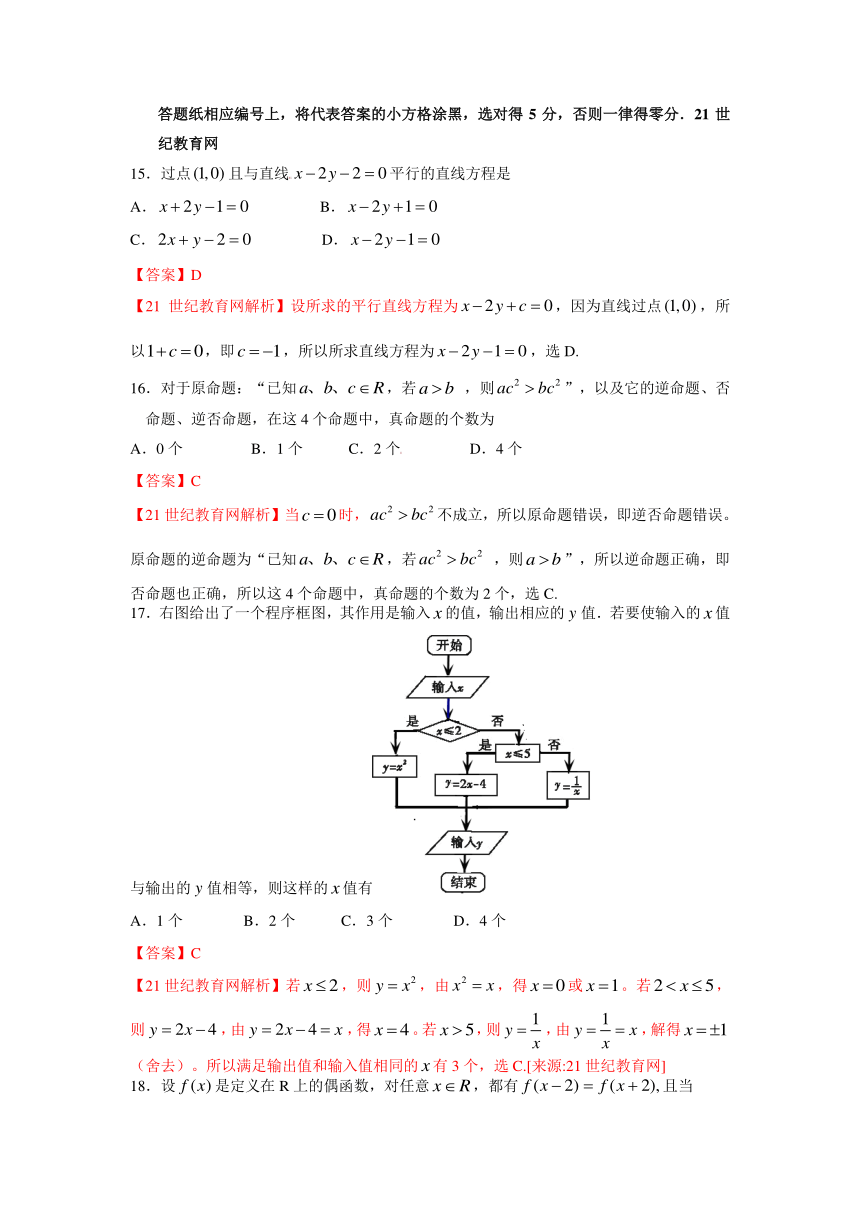
17.右图给出了一个程序框图,其作用是输入的值,输出相应的值.若要使输入的值与输出的值相等,则这样的值有
A.1个 B.2个 C.3个 D.4个
【答案】C
【21世纪教育网解析】若,则,由,得或。若,则,由,得。若,则,由,解得(舍去)。所以满足输出值和输入值相同的有3个,选C.[来源:21世纪教育网]
18.设是定义在R上的偶函数,对任意,都有且当时,.若在区间内关于的方程恰有3个不同的实数根,则实数的取值范围是
A. B. C. D.
【答案】D
【21世纪教育网解析】由得,所以函数的周期是4,又函数为偶函数,所以,即函数关于对称。且。由得,令
,做出函数的图象如图,由图象可知,要使方程恰有3个不同的实数根,则有,即,所以,即,解得,所以选D.
三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)
已知,,其中.设函数,求的最小正周期、最大值和最小值.
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分
已知,且满足.
(1)求;
(2)若,,求证:.
[来源:21世纪教育网]
21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度(单位:千克/年)是养殖密度(单位:尾/立方米)的函数.当不超过4(尾/立方米)时,的值为(千克/年);当时,是的一次函数;当达到(尾/立方米)时,因缺氧等原因,的值为(千克/年)。
(1)当时,求函数的表达式;
(2)当养殖密度为多大时,鱼的年生长量(单位:千克/立方米)可以达到最大,并求出最大值.
21世纪教育网
21世纪教育网
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分
已知递增的等差数列的首项,且、、成等比数列.
(1)求数列的通项公式;
(2)设数列对任意,都有成立,求的值.
(3)若,求证:数列中的任意一项总可以表示成其他两项之积.
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
对于双曲线,定义为其伴随曲线,记双曲线的左、右顶点为、.
(1)当时,记双曲线的半焦距为,其伴随椭圆的半焦距为,若,求双曲线的渐近线方程;
(2)若双曲线的方程为,弦轴,记直线与直线的交点为,求动点的轨迹方程;
(3)过双曲线的左焦点,且斜率为的直线与双曲线交于、两点,求证:对任意的,在伴随曲线上总存在点,使得.
松江区2012学年度第一学期高三期末考试
数学(理科)试卷参考答案
2013.1
1. 4 2. 2
3. 1 4. 20
5. 5 6.
7. 8. 2
9. 10. [来源:21世纪教育网]
11.③ 12. 21世纪教育网
13. 14. ③④
15.D 16. C 17.C 18.D
19.解:由题意知 ……………………… 3分
………………………………… 6分
∴最小正周期 ……………………8分
当,即时,………………10分
当,即时,…………12分
20.解:(1)设,则, …………2分
由
得 ……………………………4分
解得 或 ……………………………… 5分
∴或……………………………… 7分
(2)当时,
…………………… 10分
当时,
………………………13分
∴ ……………………………14分[来源:21世纪教育网]
21.解:(1)由题意:当时,; …………………………2分
当时,设,显然在是减函数,
由已知得,解得 …………………………4分
故函数= …………………………6分
(2)依题意并由(1)可得 ………8分
当时,为增函数,故; …………10分
当时,,
. …………………………12分
所以,当时, 的最大值为.
当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为千克/立方米.
…………………………14分
22.解:(1)∵是递增的等差数列,设公差为 ……………………1分
、、成等比数列,∴ ……………………2分
由 及得 ……………………………3分
∴ ……………………………4分
(2)∵, 对都成立
当时,得 ……………………………5分
当时,由①,及②
①-②得,得 …………7分
∴ ……………8分
∴ …………10分
(3)对于给定的,若存在,使得 ………11分
∵,只需, …………………12分
即,即
即, 取,则 …………………14分
∴对数列中的任意一项,都存在和
使得 ………………………16分
23.解:(1)∵, ………………………1分
由,得,即
可得 ………………………3分
∴的渐近线方程为 ………………………4分
(2)设,,又、,
∴直线的方程为…………①
直线的方程为…………② ……………………6分
由①②得 ………………………………8分
∵ 在双曲线上21世纪教育网
∴ ∴ ………………………………10分
(3)证明:点的坐标为,直线的方程为,
设、的坐标分别为、 ……………………………11分
则由 得,
即,
当时,
∵
∴, ………………………13分
由 知 ,
∴ …………………………………16分
∵双曲线的伴随曲线是圆,圆上任意一点到的距离,
∴ …………………………………17分
∵
∴对任意的,在伴随曲线上总存在点,
使得………………………………18分
数学(理科)试卷(一模)
(满分150分,完卷时间120分钟) 2013.1
一、填空题 (本大题满分56分)本大题共有14题,考生必须在答题纸相应编号的空格内直接填写结果,每个空格填对得4分,否则一律得零分.
1.已知集合,,若,则 ▲ .
【答案】4
【21世纪教育网解析】因为,所以或。若,则,,满足。若,则,,不满足,所以。
2.若行列式,则 ▲ .
【答案】2
【21世纪教育网解析】由得,即,所以。
3.若函数的图像与的图像关于直线对称,则= ▲ .
【答案】1
【21世纪教育网解析】因为函数的图像与的图像关于直线对称,所以由,即,所以,所以。
4.某林场有树苗30000棵,其中松树苗4000棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为 ▲ .
【答案】20
【21世纪教育网解析】设样本中松树苗的数量为,则有,解得。
5.已知数列的前项和,则 ▲ .
【答案】5
【21世纪教育网解析】因为,所以。
6.己知,,且,则 ▲ ..[21世纪教育网]
【答案】
【21世纪教育网解析】因为,所以,即,所以。
7.抛物线的焦点为椭圆 的右焦点,顶点在椭圆的中心,则抛物线方程为 ▲
【答案】
【21世纪教育网解析】由椭圆方程可知,所以,即,所以椭圆的右焦点为,因为抛物线的焦点为椭圆的右焦点,所以,所以。所以抛物线的方程为。
8.已知,则的最小值为 ▲ .
【答案】2
【21世纪教育网解析】由得且,即。所以,所以的最小值为2.
9.在△ABC中,角所对的边分别是,若,且,
则△ABC的面积等于 ▲ .
【答案】
【21世纪教育网解析】由得,所以,所以,所以。
10.若二项式展开式中项的系数是7,则= ▲ .
【答案】
【21世纪教育网解析】二项展开式的通项为,令得,,所以,所以的系数为,所以。所以。
11.给出四个函数:①,②,③,④,其中满足条件:对任意实数及任意正数,都有及的函数为 ▲ .(写出所有满足条件的函数的序号)
【答案】③
【21世纪教育网解析】由得,所以函数为奇函数。对任意实数及任意正数由可知,函数为增函数。①为奇函数,但在上不单调。②为偶函数。,③满足条件。④为奇函数,但在在上不单调。所以满足条件的函数的序号为③。
12.甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为,再由乙猜想甲刚才想的数字,把乙猜的数字记为,且,若,则称甲乙“心有灵犀”.现找两个人玩这个游戏,得出他们“心有灵犀”的概率为 ▲ .
【答案】
【21世纪教育网解析】试验发生的所有事件是从0,1,2,3,4,5,6,7,8,9十个数中任取两个共有10×10种不同的结果,
则的情况有0,0;1,1;2,2;3,3;4,4;5,5;6,6;7,7;8,8;9,9;0,1;1,0;1,2;2,1;2,3;3,2;3,4;4,3;4,5;5,4;5,6;6,5;6,7;7,6;7,8;8,7;8,9;9,8共28种情况,
甲乙出现的结果共有10×10=100,
所以他们”心有灵犀”的概率为P==.
13.已知是定义在上的增函数,且的图像关于点对称.若实数满足不等式,则的取值范围是 ▲ .
【答案】
【21世纪教育网解析】因为函数的图像关于点对称,所以,由得,因为函数是定义在上的增函数,所以得,即,配方得,所以圆心为,半径为1,的几何意义为圆上动点到原点距离的平方的最值。圆心到原点的距离为,所以动点到原点的距离的范围是,所以,所以的取值范围是。
14.定义变换将平面内的点变换到平面内的点.
若曲线经变换后得到曲线,曲线经变换后得到曲线,依次类推,曲线经变换后得到曲线,当时,记曲线与、轴正半轴的交点为和.某同学研究后认为曲线具有如下性质:
①对任意的,曲线都关于原点对称;
②对任意的,曲线恒过点;
③对任意的,曲线均在矩形(含边界)的内部,其中的坐标为;
④记矩形的面积为,则
其中所有正确结论的序号是 ▲ .
【答案】③④
【21世纪教育网解析】设上一点,则该点是由变换来的,所以,即。①因为,所以不可能关于原点对称,所以①错误。②当,则,所以,所以②错误。③因为,所以曲线均在矩形(含边界)的内部,所以③正确。④因为,所以,所以,所以④正确,所以所有正确结论的序号是③④。
二、选择题(本大题满分20分)本大题共有4题,每题有且只有一个正确答案,考生必须在答题纸相应编号上,将代表答案的小方格涂黑,选对得5分,否则一律得零分.21世纪教育网
15.过点且与直线平行的直线方程是
A. B.
C. D.
【答案】D
【21世纪教育网解析】设所求的平行直线方程为,因为直线过点,所以,即,所以所求直线方程为,选D.
16.对于原命题:“已知,若 ,则”,以及它的逆命题、否命题、逆否命题,在这4个命题中,真命题的个数为
A.0个 B.1个 C.2个 D.4个
【答案】C
【21世纪教育网解析】当时,不成立,所以原命题错误,即逆否命题错误。原命题的逆命题为“已知,若 ,则”,所以逆命题正确,即否命题也正确,所以这4个命题中,真命题的个数为2个,选C.
17.右图给出了一个程序框图,其作用是输入的值,输出相应的值.若要使输入的值与输出的值相等,则这样的值有
A.1个 B.2个 C.3个 D.4个
【答案】C
【21世纪教育网解析】若,则,由,得或。若,则,由,得。若,则,由,解得(舍去)。所以满足输出值和输入值相同的有3个,选C.[来源:21世纪教育网]
18.设是定义在R上的偶函数,对任意,都有且当时,.若在区间内关于的方程恰有3个不同的实数根,则实数的取值范围是
A. B. C. D.
【答案】D
【21世纪教育网解析】由得,所以函数的周期是4,又函数为偶函数,所以,即函数关于对称。且。由得,令
,做出函数的图象如图,由图象可知,要使方程恰有3个不同的实数根,则有,即,所以,即,解得,所以选D.
三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.
19.(本题满分12分)
已知,,其中.设函数,求的最小正周期、最大值和最小值.
20.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分
已知,且满足.
(1)求;
(2)若,,求证:.
[来源:21世纪教育网]
21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度(单位:千克/年)是养殖密度(单位:尾/立方米)的函数.当不超过4(尾/立方米)时,的值为(千克/年);当时,是的一次函数;当达到(尾/立方米)时,因缺氧等原因,的值为(千克/年)。
(1)当时,求函数的表达式;
(2)当养殖密度为多大时,鱼的年生长量(单位:千克/立方米)可以达到最大,并求出最大值.
21世纪教育网
21世纪教育网
22.(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分
已知递增的等差数列的首项,且、、成等比数列.
(1)求数列的通项公式;
(2)设数列对任意,都有成立,求的值.
(3)若,求证:数列中的任意一项总可以表示成其他两项之积.
23.(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分
对于双曲线,定义为其伴随曲线,记双曲线的左、右顶点为、.
(1)当时,记双曲线的半焦距为,其伴随椭圆的半焦距为,若,求双曲线的渐近线方程;
(2)若双曲线的方程为,弦轴,记直线与直线的交点为,求动点的轨迹方程;
(3)过双曲线的左焦点,且斜率为的直线与双曲线交于、两点,求证:对任意的,在伴随曲线上总存在点,使得.
松江区2012学年度第一学期高三期末考试
数学(理科)试卷参考答案
2013.1
1. 4 2. 2
3. 1 4. 20
5. 5 6.
7. 8. 2
9. 10. [来源:21世纪教育网]
11.③ 12. 21世纪教育网
13. 14. ③④
15.D 16. C 17.C 18.D
19.解:由题意知 ……………………… 3分
………………………………… 6分
∴最小正周期 ……………………8分
当,即时,………………10分
当,即时,…………12分
20.解:(1)设,则, …………2分
由
得 ……………………………4分
解得 或 ……………………………… 5分
∴或……………………………… 7分
(2)当时,
…………………… 10分
当时,
………………………13分
∴ ……………………………14分[来源:21世纪教育网]
21.解:(1)由题意:当时,; …………………………2分
当时,设,显然在是减函数,
由已知得,解得 …………………………4分
故函数= …………………………6分
(2)依题意并由(1)可得 ………8分
当时,为增函数,故; …………10分
当时,,
. …………………………12分
所以,当时, 的最大值为.
当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为千克/立方米.
…………………………14分
22.解:(1)∵是递增的等差数列,设公差为 ……………………1分
、、成等比数列,∴ ……………………2分
由 及得 ……………………………3分
∴ ……………………………4分
(2)∵, 对都成立
当时,得 ……………………………5分
当时,由①,及②
①-②得,得 …………7分
∴ ……………8分
∴ …………10分
(3)对于给定的,若存在,使得 ………11分
∵,只需, …………………12分
即,即
即, 取,则 …………………14分
∴对数列中的任意一项,都存在和
使得 ………………………16分
23.解:(1)∵, ………………………1分
由,得,即
可得 ………………………3分
∴的渐近线方程为 ………………………4分
(2)设,,又、,
∴直线的方程为…………①
直线的方程为…………② ……………………6分
由①②得 ………………………………8分
∵ 在双曲线上21世纪教育网
∴ ∴ ………………………………10分
(3)证明:点的坐标为,直线的方程为,
设、的坐标分别为、 ……………………………11分
则由 得,
即,
当时,
∵
∴, ………………………13分
由 知 ,
∴ …………………………………16分
∵双曲线的伴随曲线是圆,圆上任意一点到的距离,
∴ …………………………………17分
∵
∴对任意的,在伴随曲线上总存在点,
使得………………………………18分
同课章节目录
