多边形的内角和
图片预览





文档简介
课件17张PPT。多边形的内角和复习回顾1、什么是多边形?
2、多边形的内角,四边形有几个内角?
五边形有几个内角?n边形有几个内
角?
3、多边形的对角线,n边形从一个顶点
出发可以引多少条对角线?它们将n
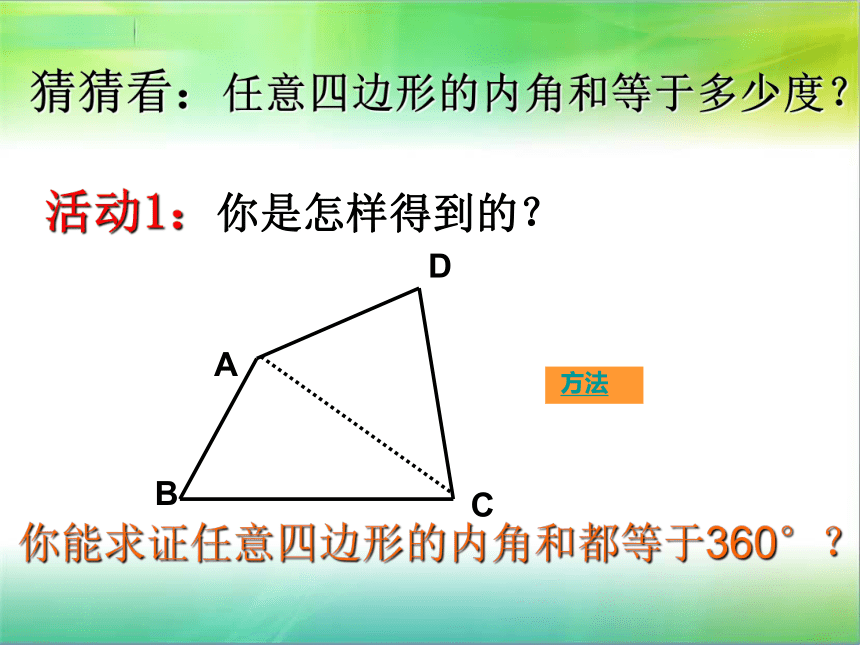
边形分为多少个三角形? 三角形的内角和等于180°正方形,长方形的内角和都是360°你能求出梯形、平行四边形的内角和度数吗?猜猜看:任意四边形的内角和等于多少度? 活动1:你是怎样得到的?你能求证任意四边形的内角和都等于360°?1234
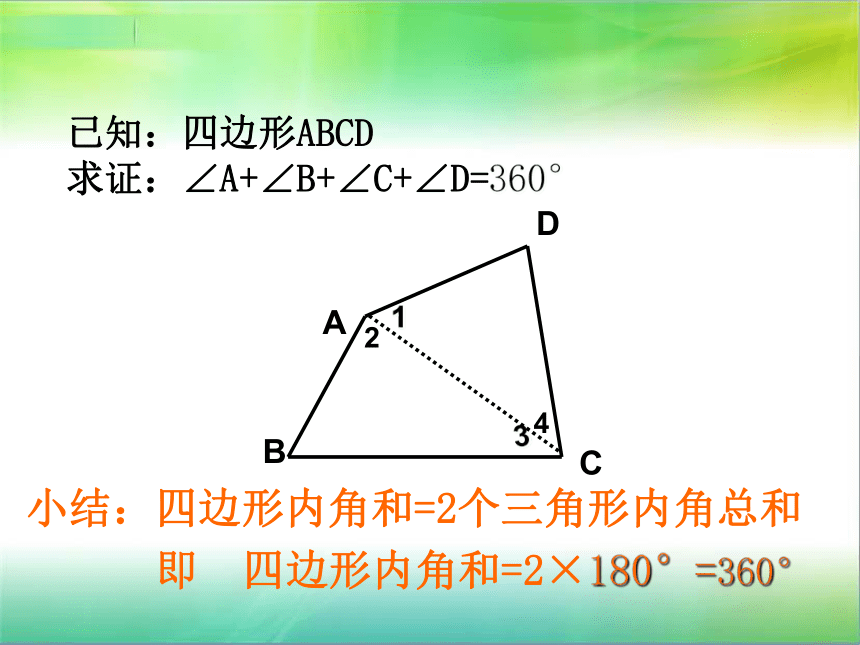
已知:四边形ABCD 求证:∠A+∠B+∠C+∠D=360°小结:四边形内角和=2个三角形内角总和
即 四边形内角和=2×180°=360°
活动2:选择此种方法分别求出任意五边形、六边形的内角和等于多少度?3×180°=540°4×180°=720° 四边形 五边形 六边形从四边形的一个顶点出发,可以引 条对角线,它们将四边形分
为 个三角形,四边形的内角和等于 。从五边形的一个顶点出发,可以引 条对角线,它们将五边形分
为 个三角形,五边形的内角和等于 。 从六边形的一个顶点出发,可以引 条对角线,它们将六边形分
为 个三角形,六边形的内角和等于 。 12(4-2)×180 °23(5-2)×180 °34(6-2)×180 °通过以上过程,你能发现所分三角形个数与边数的关系吗?n边形内角和=(n-2)×180°活动3:类比四边形、五边形、六边形内角和的推导过程,求
n边形的内角和。A1A2A3A4A5A6A7An从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于 。 n-3n-2(n-2)×180 ° N边形内角和=
(n-2)×180°
练习1:你能说出七边形的内角和吗? 十边形呢? 解:七边形内角和:
(7-2)×180°=900°十边形内角和:
(10-2)× 180°
= 1440°
练习2: 一个多边形的内角和等于1260°, 它是几边形?解1:设这个多边形是n边形,依题意得,
(n-2)×180°=1260°
解得:n=9解2:1260°÷180°+2
=7+2
=9
答:这个多边形是九边形。课堂 小结:n边形内角和 =(n-2)×180°
边数n = n边形内角和÷180°+2
例题:如果一个四边形的一组对角互补,那么另一 组对角有什么关系?解:如图所示,四边形ABCD中,
∠A+∠C=180°
因为
∠A+∠B+ ∠C+ ∠D=(4-2)×180° =360°
所以
∠B+ ∠D =360°-( ∠A+∠C )
=360°- 180°
=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。课后作业:课本P84 :2、5题 一个多边形减去一个内角后,其余各内角和2012°,求这个多边形的边数 。思考题
180°×2=360°180°×3 -180°=360°180°×4 -360°=360°PP
2、多边形的内角,四边形有几个内角?
五边形有几个内角?n边形有几个内
角?
3、多边形的对角线,n边形从一个顶点
出发可以引多少条对角线?它们将n
边形分为多少个三角形? 三角形的内角和等于180°正方形,长方形的内角和都是360°你能求出梯形、平行四边形的内角和度数吗?猜猜看:任意四边形的内角和等于多少度? 活动1:你是怎样得到的?你能求证任意四边形的内角和都等于360°?1234
已知:四边形ABCD 求证:∠A+∠B+∠C+∠D=360°小结:四边形内角和=2个三角形内角总和
即 四边形内角和=2×180°=360°
活动2:选择此种方法分别求出任意五边形、六边形的内角和等于多少度?3×180°=540°4×180°=720° 四边形 五边形 六边形从四边形的一个顶点出发,可以引 条对角线,它们将四边形分
为 个三角形,四边形的内角和等于 。从五边形的一个顶点出发,可以引 条对角线,它们将五边形分
为 个三角形,五边形的内角和等于 。 从六边形的一个顶点出发,可以引 条对角线,它们将六边形分
为 个三角形,六边形的内角和等于 。 12(4-2)×180 °23(5-2)×180 °34(6-2)×180 °通过以上过程,你能发现所分三角形个数与边数的关系吗?n边形内角和=(n-2)×180°活动3:类比四边形、五边形、六边形内角和的推导过程,求
n边形的内角和。A1A2A3A4A5A6A7An从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于 。 n-3n-2(n-2)×180 ° N边形内角和=
(n-2)×180°
练习1:你能说出七边形的内角和吗? 十边形呢? 解:七边形内角和:
(7-2)×180°=900°十边形内角和:
(10-2)× 180°
= 1440°
练习2: 一个多边形的内角和等于1260°, 它是几边形?解1:设这个多边形是n边形,依题意得,
(n-2)×180°=1260°
解得:n=9解2:1260°÷180°+2
=7+2
=9
答:这个多边形是九边形。课堂 小结:n边形内角和 =(n-2)×180°
边数n = n边形内角和÷180°+2
例题:如果一个四边形的一组对角互补,那么另一 组对角有什么关系?解:如图所示,四边形ABCD中,
∠A+∠C=180°
因为
∠A+∠B+ ∠C+ ∠D=(4-2)×180° =360°
所以
∠B+ ∠D =360°-( ∠A+∠C )
=360°- 180°
=180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。课后作业:课本P84 :2、5题 一个多边形减去一个内角后,其余各内角和2012°,求这个多边形的边数 。思考题
180°×2=360°180°×3 -180°=360°180°×4 -360°=360°PP
