北师大版(2019)高中数学 必修第二册 1.4.4诱导公式与旋转 教案
文档属性
| 名称 | 北师大版(2019)高中数学 必修第二册 1.4.4诱导公式与旋转 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 22.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-20 14:34:43 | ||
图片预览

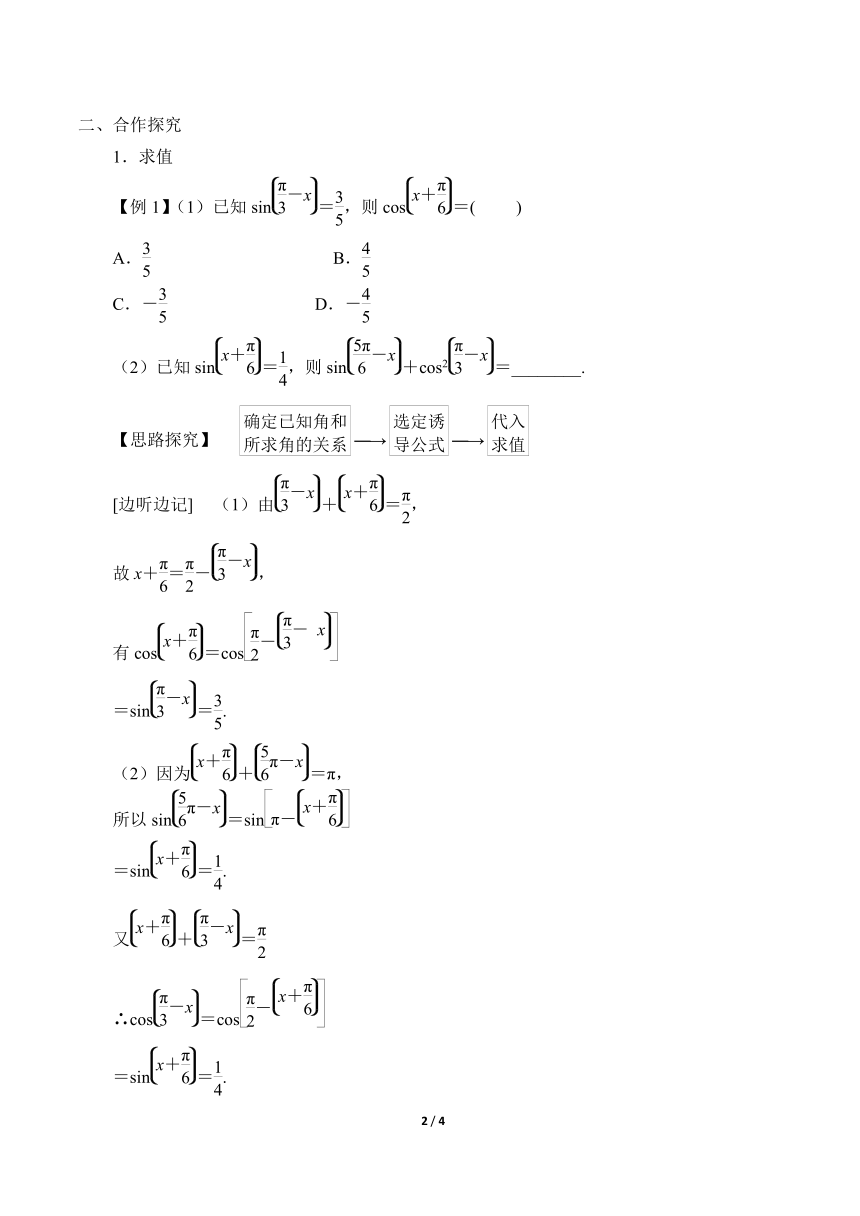
文档简介
诱导公式与旋转
【教学目标】
1.根据角的终边的旋转关系,推导并掌握对应的诱导公式.
2.对所有诱导公式进行综合应用.
【教学重难点】
诱导公式的应用.
【教学过程】
一、基础铺垫
1.诱导公式与旋转:
sin=cos α,cos=-sin α.
sin=cos α,cos=sin α.
2.对正弦、余弦函数诱导公式的理解
(1)利用诱导公式,可以将任意角的正弦、余弦函数问题转化为锐角的正弦、余弦函数问题.具体步骤是:首先将任意负角的三角函数利用公式转化为任意正角的三角函数,其次转化为0°~360°的三角函数,然后转化为锐角的三角函数,最后运用特殊角的三角函数值求值.步骤可简记为“负化正,大化小,化到锐角再求值”.如:
cos=cos =cos=cos =cos=-cos =-.
(2)所有诱导公式可用口诀“奇变偶不变,符号看象限”来记忆,其中:
①“变”与“不变”是指等式两边的三角函数名是否改变.
②“奇”“偶”是对k·±α中的整数k来讲的.
③“象限”指k·±α中,将α看作锐角时,k·±α所在象限,再根据“一全正,二正弦,四余弦”的符号规律确定原函数值符号.
例如,将cos写成cos,因为1是奇数,则“cos”变为正弦函数符号“sin”,又将α看作锐角时,+α是第二象限角,cos的符号为“-”,故有cos=-sin α.
二、合作探究
1.求值
【例1】(1)已知sin=,则cos=( )
A. B.
C.- D.-
(2)已知sin=,则sin+cos2=________.
【思路探究】 ―→―→
[边听边记] (1)由+=,
故x+=-,
有cos=cos
=sin=.
(2)因为+=π,
所以sin=sin
=sin=.
又+=
∴cos=cos
=sin=.
所以sin+cos2
=+=.
【规律方法】
(1)解答这类求值的问题,首先应把所给的值进行化简,再结合被求值的式子的特点,观察所给值的式子与被求式的特点,找出它们之间的内在联系,特别是角之间的关系,恰当地选择诱导公式.
(2)常见的角之间的关系有+=;
+=;A+B+C=π,=(A,B,C是△ABC的三个内角)等.
[变式训练]
1.(1)已知sin=,那么cos α=( )
A.- B.-
C. D.
(2)已知cos=,求cos的值.
解析: (1)sin=sin
=sin=cos α=.
(2)cos=cos
=-cos=-.
2.利用诱导公式化简
【例2】化简:.
[解]原式=
==
==-1.
【规律方法】
三角函数式的化简是对式子进行某种变形以清晰地显示式子中所有项之间的关系,其变形过程就是统一角、统一函数名称的过程,所以对式子变形时,一方面要注意角与角之间的关系,另一方面要根据不同的变形目的,对公式进行合理选择.化简的基本要求是:(1)能求出值的求出值;(2)使三角函数名称尽量少;(3)使项数尽量少;(4)使次数尽量低;(5)使分母尽量不含三角函数;(6)使被开方数(式)尽量不含三角函数.
1 / 3
【教学目标】
1.根据角的终边的旋转关系,推导并掌握对应的诱导公式.
2.对所有诱导公式进行综合应用.
【教学重难点】
诱导公式的应用.
【教学过程】
一、基础铺垫
1.诱导公式与旋转:
sin=cos α,cos=-sin α.
sin=cos α,cos=sin α.
2.对正弦、余弦函数诱导公式的理解
(1)利用诱导公式,可以将任意角的正弦、余弦函数问题转化为锐角的正弦、余弦函数问题.具体步骤是:首先将任意负角的三角函数利用公式转化为任意正角的三角函数,其次转化为0°~360°的三角函数,然后转化为锐角的三角函数,最后运用特殊角的三角函数值求值.步骤可简记为“负化正,大化小,化到锐角再求值”.如:
cos=cos =cos=cos =cos=-cos =-.
(2)所有诱导公式可用口诀“奇变偶不变,符号看象限”来记忆,其中:
①“变”与“不变”是指等式两边的三角函数名是否改变.
②“奇”“偶”是对k·±α中的整数k来讲的.
③“象限”指k·±α中,将α看作锐角时,k·±α所在象限,再根据“一全正,二正弦,四余弦”的符号规律确定原函数值符号.
例如,将cos写成cos,因为1是奇数,则“cos”变为正弦函数符号“sin”,又将α看作锐角时,+α是第二象限角,cos的符号为“-”,故有cos=-sin α.
二、合作探究
1.求值
【例1】(1)已知sin=,则cos=( )
A. B.
C.- D.-
(2)已知sin=,则sin+cos2=________.
【思路探究】 ―→―→
[边听边记] (1)由+=,
故x+=-,
有cos=cos
=sin=.
(2)因为+=π,
所以sin=sin
=sin=.
又+=
∴cos=cos
=sin=.
所以sin+cos2
=+=.
【规律方法】
(1)解答这类求值的问题,首先应把所给的值进行化简,再结合被求值的式子的特点,观察所给值的式子与被求式的特点,找出它们之间的内在联系,特别是角之间的关系,恰当地选择诱导公式.
(2)常见的角之间的关系有+=;
+=;A+B+C=π,=(A,B,C是△ABC的三个内角)等.
[变式训练]
1.(1)已知sin=,那么cos α=( )
A.- B.-
C. D.
(2)已知cos=,求cos的值.
解析: (1)sin=sin
=sin=cos α=.
(2)cos=cos
=-cos=-.
2.利用诱导公式化简
【例2】化简:.
[解]原式=
==
==-1.
【规律方法】
三角函数式的化简是对式子进行某种变形以清晰地显示式子中所有项之间的关系,其变形过程就是统一角、统一函数名称的过程,所以对式子变形时,一方面要注意角与角之间的关系,另一方面要根据不同的变形目的,对公式进行合理选择.化简的基本要求是:(1)能求出值的求出值;(2)使三角函数名称尽量少;(3)使项数尽量少;(4)使次数尽量低;(5)使分母尽量不含三角函数;(6)使被开方数(式)尽量不含三角函数.
1 / 3
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
