苏科版数学八年级上册第二章勾股定理和平方根2.5 实数复习课件(21ppt)
文档属性
| 名称 | 苏科版数学八年级上册第二章勾股定理和平方根2.5 实数复习课件(21ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 506.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-03-03 00:00:00 | ||
图片预览






文档简介
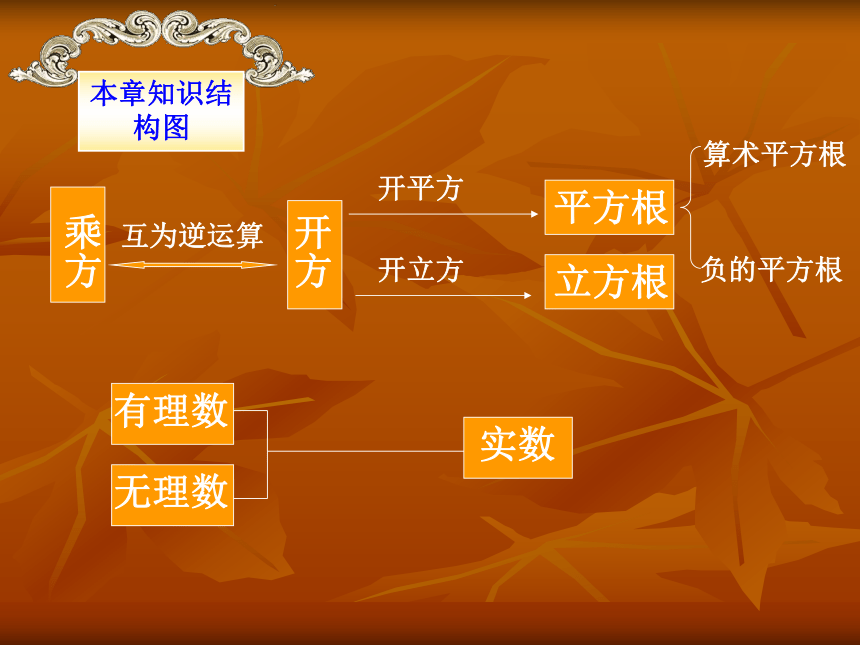
课件21张PPT。实数复习(一)本章知识结构图乘方开方开平方开立方平方根立方根有理数无理数实数互为逆运算算术平方根负的平方根平方根、立方根概念及性质1.算术平方根的定义:一般地,如果一个正数x的平方等于
a,即 =a,那么这个正数x叫做a的
算术平方根。a的算术平方根记为 ,
读作“根号a”,a叫做被开方数。
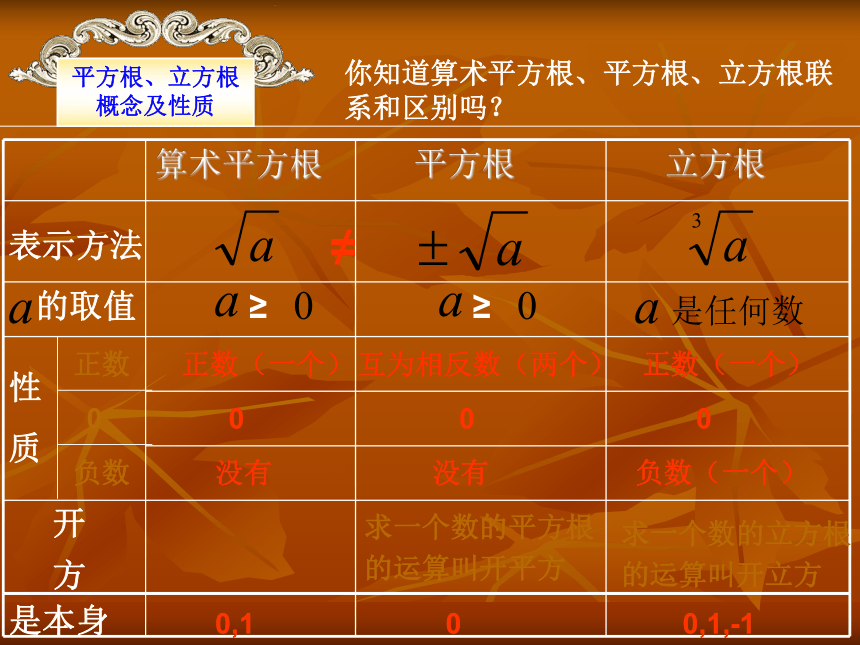
特殊:0的算术平方根是0。一般地,如果一个数的平方等于a ,那么这个数就叫做a 的平方根(或二次方根). 这就是说,如果x 2 = a ,那么 x 就叫做 a 的平方根.a的平方根记为± 2. 平方根的定义:3.平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。平方根、立方根概念及性质4.立方根的定义:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作 .5.立方根的性质:平方根、立方根概念及性质你知道算术平方根、平方根、立方根联系和区别吗?表示方法的取值性
质≥开
方≥正数0负数正数(一个)0没有互为相反数(两个)0没有正数(一个)0负数(一个)求一个数的平方根
的运算叫开平方求一个数的立方根
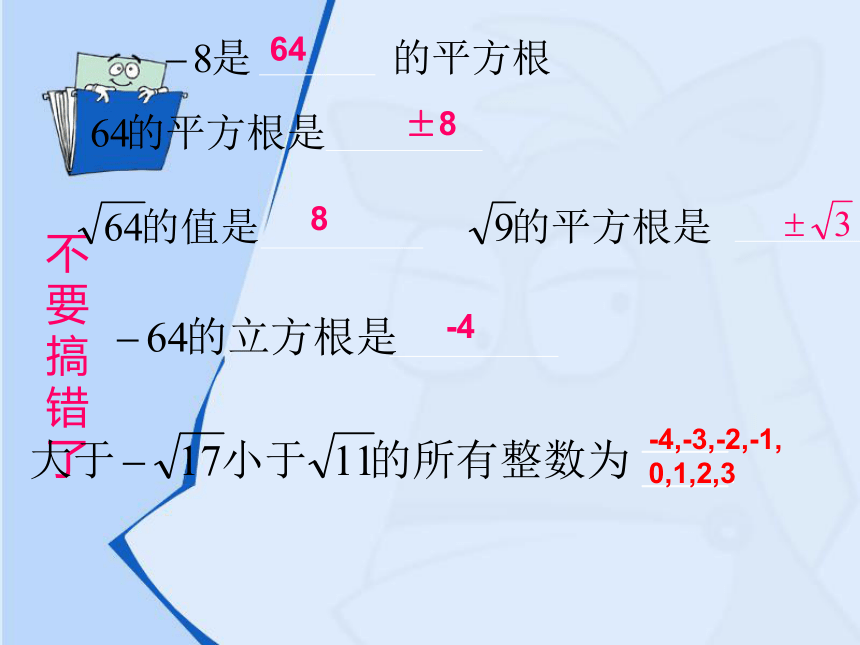
的运算叫开立方≠是本身0,100,1,-1=你知道吗?课后练习题1.求下列各数的算术平方根:(1) 0.04;(2) 1; (3) 56 ; (4) (-3)2 ; (5) 3.求下列各数的立方根:(1) 121;(2) 16; (3) 0 ; (4) (-3)2 ; (5) 2.求下列各数的平方根:(1) -0.008;(2) 43; (3) -64; (4) (-3)3; (5) 4.求下列各式的值:求根也好,求值也好,关键要弄清它是什么意思,然后可以选择定义和性质来求.不要搞错了64±88-4______.-4,-3,-2,-1,
0,1,2,3不要遗漏哦!解下列方程:当方程中出现平方时,若有解,一般都有两个解当方程中出现立方时,一般都有一个解1.解:2.解:掌握规律 注意平方根和立方根的移位法则1、无限不循环的小数 叫做无理数. 有理数和无理数统称实数. 4、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样6、在进行实数的运算时,有理数的运算法则及运算性质同样适用。实数的有关概念和性质2、实数与数轴上的点是一一对应的.3、同样的,平面直角坐标系中的点与有序实数对是一一对应的.5、实数的大小比较方法有:利用数轴比较、利用绝对值比较、求平方比较、求差比较、求商比较和计算近似值比较等方法。实数有理数无理数分数整数正整数 0负整数正分数负分数自然数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况是负数等于它的相反数是正数等于它本身是负数里面的数的符号
化简绝对值要看它等于它的相反数要学会计算哟!计算:
1、2、(结果保留3个有效数字)注意:计算过程中要多保留一位!如图是两个边长1的正方形操作探索拼成的长方形, 其面积是2. 现剪下两个角重新拼成一个 正方形, 新正方形的边长是_____ 下图数轴中, 正方形的对角线长为____, 以原点为圆心, 对角线长为半径画弧截得一点, 该点与原点的距离是____, 该点表示的数是____. 实数与数轴上的点是一一对应关系.0132-1-2问题:边长为1的正方形,对角线长为多少?操作探索 平面直角坐标系中的点与有序实数对是一一对应的.-3123-1-2xyABCD 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。实数的大小比较方法多种,要具体观察实数的特点,灵活选择最好的比较方法 通过这节课的学习,你有何收获?回顾我们大家来总结!再见!
a,即 =a,那么这个正数x叫做a的
算术平方根。a的算术平方根记为 ,
读作“根号a”,a叫做被开方数。
特殊:0的算术平方根是0。一般地,如果一个数的平方等于a ,那么这个数就叫做a 的平方根(或二次方根). 这就是说,如果x 2 = a ,那么 x 就叫做 a 的平方根.a的平方根记为± 2. 平方根的定义:3.平方根的性质:
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。平方根、立方根概念及性质4.立方根的定义:
一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作 .5.立方根的性质:平方根、立方根概念及性质你知道算术平方根、平方根、立方根联系和区别吗?表示方法的取值性
质≥开
方≥正数0负数正数(一个)0没有互为相反数(两个)0没有正数(一个)0负数(一个)求一个数的平方根
的运算叫开平方求一个数的立方根
的运算叫开立方≠是本身0,100,1,-1=你知道吗?课后练习题1.求下列各数的算术平方根:(1) 0.04;(2) 1; (3) 56 ; (4) (-3)2 ; (5) 3.求下列各数的立方根:(1) 121;(2) 16; (3) 0 ; (4) (-3)2 ; (5) 2.求下列各数的平方根:(1) -0.008;(2) 43; (3) -64; (4) (-3)3; (5) 4.求下列各式的值:求根也好,求值也好,关键要弄清它是什么意思,然后可以选择定义和性质来求.不要搞错了64±88-4______.-4,-3,-2,-1,
0,1,2,3不要遗漏哦!解下列方程:当方程中出现平方时,若有解,一般都有两个解当方程中出现立方时,一般都有一个解1.解:2.解:掌握规律 注意平方根和立方根的移位法则1、无限不循环的小数 叫做无理数. 有理数和无理数统称实数. 4、在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样6、在进行实数的运算时,有理数的运算法则及运算性质同样适用。实数的有关概念和性质2、实数与数轴上的点是一一对应的.3、同样的,平面直角坐标系中的点与有序实数对是一一对应的.5、实数的大小比较方法有:利用数轴比较、利用绝对值比较、求平方比较、求差比较、求商比较和计算近似值比较等方法。实数有理数无理数分数整数正整数 0负整数正分数负分数自然数正无理数负无理数无限不循环小数有限小数及无限循环小数一般有三种情况是负数等于它的相反数是正数等于它本身是负数里面的数的符号
化简绝对值要看它等于它的相反数要学会计算哟!计算:
1、2、(结果保留3个有效数字)注意:计算过程中要多保留一位!如图是两个边长1的正方形操作探索拼成的长方形, 其面积是2. 现剪下两个角重新拼成一个 正方形, 新正方形的边长是_____ 下图数轴中, 正方形的对角线长为____, 以原点为圆心, 对角线长为半径画弧截得一点, 该点与原点的距离是____, 该点表示的数是____. 实数与数轴上的点是一一对应关系.0132-1-2问题:边长为1的正方形,对角线长为多少?操作探索 平面直角坐标系中的点与有序实数对是一一对应的.-3123-1-2xyABCD 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。实数的大小比较方法多种,要具体观察实数的特点,灵活选择最好的比较方法 通过这节课的学习,你有何收获?回顾我们大家来总结!再见!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
