2021-2022学年度湘教版九年级数学下册 1.5.1 利用二次函数解决几何图形问题及实物抛物线问题 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版九年级数学下册 1.5.1 利用二次函数解决几何图形问题及实物抛物线问题 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第1章
二次函数
九年级数学湘教版·下册
1.5.1 利用二次函数解决几何图形问题及实物抛物线问题
授课人:XXXX
2.利用二次函数解决几何图形问题.(难点)
教学目标
1.通过分析实际问题中变量之间的关系,建立二次函数模型.(难点)
3.利用二次函数解决实物抛物线问题.(难点)
新课导入
前面我们学习了利用二次函数解决棒球、铅球等球类在空中运动的轨迹问题.下面学习通过建立二次函数模型解决几何问题.
新知探究
一、利用二次函数解决抛物线型问题
分析:
新知探究
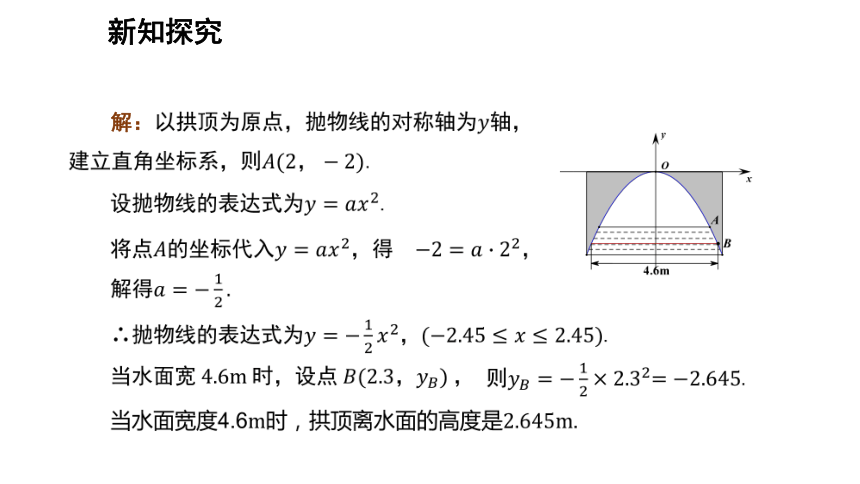
解:
新知探究
利用二次函数解决抛物线型问题的方法
(1)根据题意建立二次函数模型(若需要自己建立平面直角坐标系,则以使解决问题简便为原则);
(2)根据题目中的条件,求出抛物线的解析式(写出自变量的取值范围);
(3)根据二次函数的图象和性质解决问题;
(4)通过验证得出实际问题的答案.
新知探究
分析:
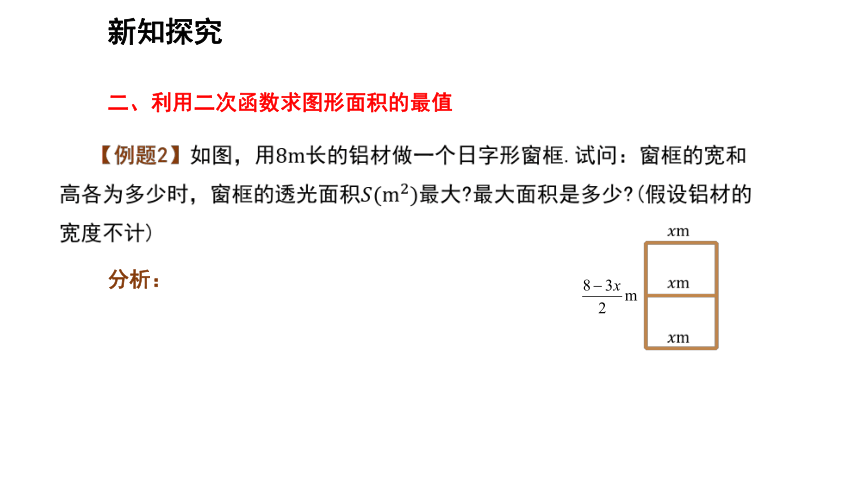
二、利用二次函数求图形面积的最值
新知探究
解:
新知探究
利用二次函数求图形面积最值问题的方法
①顶点的横坐标在自变量的取值范围之内时,最值就在顶点处取得;
②顶点的横坐标不在自变量的取值范围之内时,则根据二次函数的增减性结合自变量的取值范围来确定最值.
(1)根据题目中的数量关系建立二次函数模型,求出二次函数的解析式;
(2)根据二次函数的图象和性质确定最值:
新知探究
分析:
新知探究
解:
本课小结
一、利用二次函数解决抛物线型问题的方法
(1)根据题意建立二次函数模型(若需要自己建立平面直角坐标系,则以使解决问题简便为原则);
(2)根据题目中的条件,求出抛物线的解析式(写出自变量的取值范围);
(3)根据二次函数的图象和性质解决问题;
(4)通过验证得出实际问题的答案.
本课小结
二、利用二次函数求图形面积最值问题的方法
①顶点的横坐标在自变量的取值范围之内时,最值就在顶点处取得;
②顶点的横坐标不在自变量的取值范围之内时,则根据二次函数的增减性结合自变量的取值范围来确定最值.
(1)根据题目中的数量关系建立二次函数模型,求出二次函数的解析式;
(2)根据二次函数的图象和性质确定最值:
课堂小测
课堂小测
2.某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解:(1)设矩形一边长为x,则另一边长为(6-x),
∴S=x(6-x)=-x2+6x,其中0课堂小测
∴当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元)
(2)S=-x2+6x=-(x-3) +9.
第1章
二次函数
九年级数学湘教版·下册
1.5.1 利用二次函数解决几何图形问题及实物抛物线问题
授课人:XXXX
2.利用二次函数解决几何图形问题.(难点)
教学目标
1.通过分析实际问题中变量之间的关系,建立二次函数模型.(难点)
3.利用二次函数解决实物抛物线问题.(难点)
新课导入
前面我们学习了利用二次函数解决棒球、铅球等球类在空中运动的轨迹问题.下面学习通过建立二次函数模型解决几何问题.
新知探究
一、利用二次函数解决抛物线型问题
分析:
新知探究
解:
新知探究
利用二次函数解决抛物线型问题的方法
(1)根据题意建立二次函数模型(若需要自己建立平面直角坐标系,则以使解决问题简便为原则);
(2)根据题目中的条件,求出抛物线的解析式(写出自变量的取值范围);
(3)根据二次函数的图象和性质解决问题;
(4)通过验证得出实际问题的答案.
新知探究
分析:
二、利用二次函数求图形面积的最值
新知探究
解:
新知探究
利用二次函数求图形面积最值问题的方法
①顶点的横坐标在自变量的取值范围之内时,最值就在顶点处取得;
②顶点的横坐标不在自变量的取值范围之内时,则根据二次函数的增减性结合自变量的取值范围来确定最值.
(1)根据题目中的数量关系建立二次函数模型,求出二次函数的解析式;
(2)根据二次函数的图象和性质确定最值:
新知探究
分析:
新知探究
解:
本课小结
一、利用二次函数解决抛物线型问题的方法
(1)根据题意建立二次函数模型(若需要自己建立平面直角坐标系,则以使解决问题简便为原则);
(2)根据题目中的条件,求出抛物线的解析式(写出自变量的取值范围);
(3)根据二次函数的图象和性质解决问题;
(4)通过验证得出实际问题的答案.
本课小结
二、利用二次函数求图形面积最值问题的方法
①顶点的横坐标在自变量的取值范围之内时,最值就在顶点处取得;
②顶点的横坐标不在自变量的取值范围之内时,则根据二次函数的增减性结合自变量的取值范围来确定最值.
(1)根据题目中的数量关系建立二次函数模型,求出二次函数的解析式;
(2)根据二次函数的图象和性质确定最值:
课堂小测
课堂小测
2.某广告公司设计一幅周长为12m的矩形广告牌,广告设计费用每平方米1000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的关系式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解:(1)设矩形一边长为x,则另一边长为(6-x),
∴S=x(6-x)=-x2+6x,其中0
∴当x=3时,即矩形的一边长为3m时,矩形面积最大,为9m2.
这时设计费最多,为9×1000=9000(元)
(2)S=-x2+6x=-(x-3) +9.
