2021-2022学年度湘教版九年级数学下册 2.1 圆的对称性 课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版九年级数学下册 2.1 圆的对称性 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 15:21:48 | ||
图片预览




文档简介
(共17张PPT)
第2章
圆
九年级数学湘教版·下册
2.1 圆的对称性
授课人:XXXX
1.认识并理解圆的两种概念.(重点)
教学目标
2.掌握点和圆的位置关系.(重点)
3.认识弦、直径、弧、优弧、劣弧、等圆、等弧等与圆有关的概念,并了解它们之间的区别和联系.(难点)
4.掌握点和圆的对称性.(难点)
新课导入
在我们的生活中,经常会看到圆的形象(如图).
新知探究
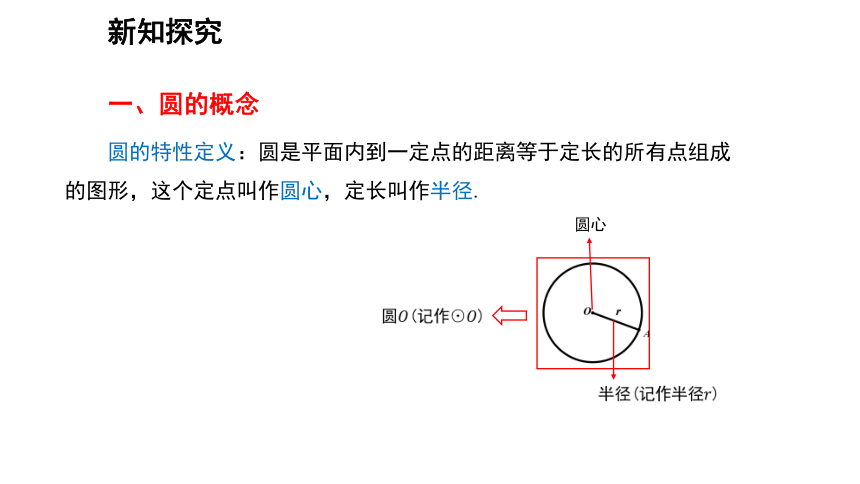
一、圆的概念
圆的特性定义:圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径.
圆心
新知探究
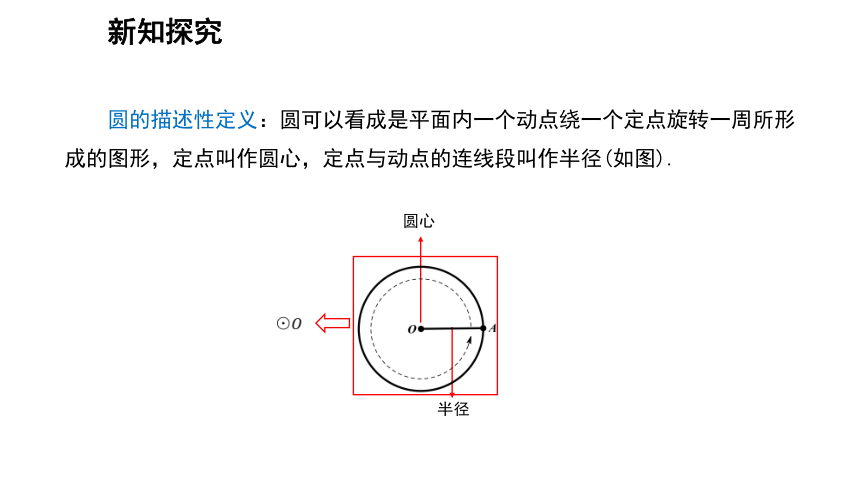
圆的描述性定义:圆可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径(如图).
圆心
半径
新知探究
二、点和圆的位置关系
到圆心的距离等于半径的点叫作圆上的点;
到圆心的距离小于半径的点叫作圆内的点;
到圆心的距离大于半径的点叫作圆外的点.
平面内点和圆的位置关系有三种:
①点在圆内;
②点在圆上;
③点在圆外.
新知探究
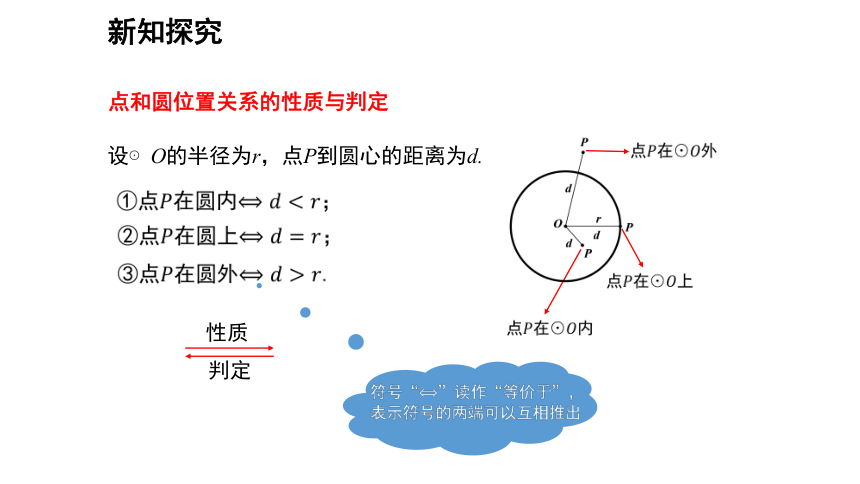
点和圆位置关系的性质与判定
设⊙O的半径为r,点P到圆心的距离为d.
性质
判定
新知探究
三、与圆有关的概念
连接圆上任意两点的线段叫作弦,
经过圆心的弦叫作直径.
圆上任意两点间的部分叫作圆弧,简称弧,
直径
弦
弧用符号“⌒”表示
新知探究
能够互相重合的两个圆叫作等圆.
能够互相重合的弧叫作等弧.
新知探究
1.圆绕圆心旋转任意角度,都能与自身重合(旋转不变性).
2.圆是中心对称图形,圆心是它的对称中心.
四、圆的对称性
3.圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
把车轮做成圆形的原因:(1)圆形易滚动;(2)车轮上各点到车轮中
心轴(圆心)的距离都等于车轮的半径,当车轮滚动时,车轮轴到地面的距离保
持不变,车能非常平稳地运行.
新知探究
【例题1】为什么通常要把车轮设计成圆形 请说说理由.
解:
新知探究
【例题2】如图,已知矩形ABCD的边AB=3,AD=4. 以A为圆心,4为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
解:
∵AD=4=r,∴D点在⊙A上.
∵AB=3∵AC=5>r,∴C点在⊙A外.
本课小结
一、圆的概念
圆的特性定义:圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径.
圆的描述性定义:圆可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径.
二、点和圆的位置关系
设⊙O的半径为r,点P到圆心的距离为d.
本课小结
1.圆绕圆心旋转任意角度,都能与自身重合(旋转不变性).
2.圆是中心对称图形,圆心是它的对称中心.
三、圆的对称性
3.圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
1. ⊙O的半径为10cm,A,B,C三点到圆心的距离分别为8cm,10cm,12cm,则点A,B,C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
课堂小测
2. ⊙O的半径r为5,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为 ( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.在⊙O上或⊙O外
圆内
圆上
圆外
B
课堂小测
3.判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
×
×
×
×
×
√
√
第2章
圆
九年级数学湘教版·下册
2.1 圆的对称性
授课人:XXXX
1.认识并理解圆的两种概念.(重点)
教学目标
2.掌握点和圆的位置关系.(重点)
3.认识弦、直径、弧、优弧、劣弧、等圆、等弧等与圆有关的概念,并了解它们之间的区别和联系.(难点)
4.掌握点和圆的对称性.(难点)
新课导入
在我们的生活中,经常会看到圆的形象(如图).
新知探究
一、圆的概念
圆的特性定义:圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径.
圆心
新知探究
圆的描述性定义:圆可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径(如图).
圆心
半径
新知探究
二、点和圆的位置关系
到圆心的距离等于半径的点叫作圆上的点;
到圆心的距离小于半径的点叫作圆内的点;
到圆心的距离大于半径的点叫作圆外的点.
平面内点和圆的位置关系有三种:
①点在圆内;
②点在圆上;
③点在圆外.
新知探究
点和圆位置关系的性质与判定
设⊙O的半径为r,点P到圆心的距离为d.
性质
判定
新知探究
三、与圆有关的概念
连接圆上任意两点的线段叫作弦,
经过圆心的弦叫作直径.
圆上任意两点间的部分叫作圆弧,简称弧,
直径
弦
弧用符号“⌒”表示
新知探究
能够互相重合的两个圆叫作等圆.
能够互相重合的弧叫作等弧.
新知探究
1.圆绕圆心旋转任意角度,都能与自身重合(旋转不变性).
2.圆是中心对称图形,圆心是它的对称中心.
四、圆的对称性
3.圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
把车轮做成圆形的原因:(1)圆形易滚动;(2)车轮上各点到车轮中
心轴(圆心)的距离都等于车轮的半径,当车轮滚动时,车轮轴到地面的距离保
持不变,车能非常平稳地运行.
新知探究
【例题1】为什么通常要把车轮设计成圆形 请说说理由.
解:
新知探究
【例题2】如图,已知矩形ABCD的边AB=3,AD=4. 以A为圆心,4为半径作⊙A,则点B,C,D与⊙A的位置关系如何?
解:
∵AD=4=r,∴D点在⊙A上.
∵AB=3
本课小结
一、圆的概念
圆的特性定义:圆是平面内到一定点的距离等于定长的所有点组成的图形,这个定点叫作圆心,定长叫作半径.
圆的描述性定义:圆可以看成是平面内一个动点绕一个定点旋转一周所形成的图形,定点叫作圆心,定点与动点的连线段叫作半径.
二、点和圆的位置关系
设⊙O的半径为r,点P到圆心的距离为d.
本课小结
1.圆绕圆心旋转任意角度,都能与自身重合(旋转不变性).
2.圆是中心对称图形,圆心是它的对称中心.
三、圆的对称性
3.圆是轴对称图形,任意一条直径所在的直线都是圆的对称轴.
1. ⊙O的半径为10cm,A,B,C三点到圆心的距离分别为8cm,10cm,12cm,则点A,B,C与⊙O的位置关系是:点A在 ;点B在 ;点C在 .
课堂小测
2. ⊙O的半径r为5,O为原点,点P的坐标为(3,4),则点P与⊙O的位置关系为 ( )
A.在⊙O内 B.在⊙O上 C.在⊙O外 D.在⊙O上或⊙O外
圆内
圆上
圆外
B
课堂小测
3.判断下列说法的正误:
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
×
×
×
×
×
√
√
