2021-2022学年度湘教版九年级数学下册课件 2.2.2.1 圆周角定理及推论(共18张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版九年级数学下册课件 2.2.2.1 圆周角定理及推论(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 13:37:55 | ||
图片预览




文档简介
(共18张PPT)
第2章
圆
九年级数学湘教版·下册
2.2.2.1 圆周角定理及推论1
授课人:XXXX
1.理解圆周角的概念,会叙述并证明圆周角定理.
教学目标
2.能运用圆周角定理解决简单的几何问题.(重点、难点)
3.理解掌握圆周角定理的推论1,并能熟练运用.(难点)
新课导入
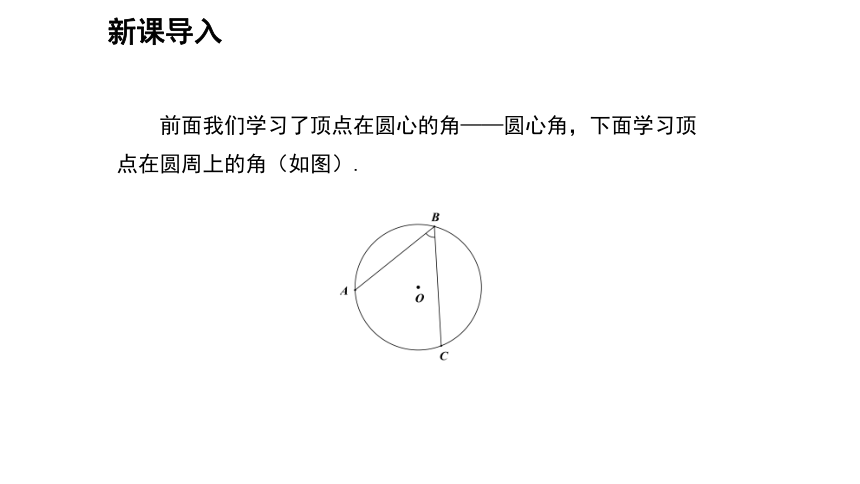
前面我们学习了顶点在圆心的角——圆心角,下面学习顶点在圆周上的角(如图).
新知探究
一、圆周角
顶点在圆上,且角的两边与圆相交的角叫作圆周角.
①
②
④
③
新知探究
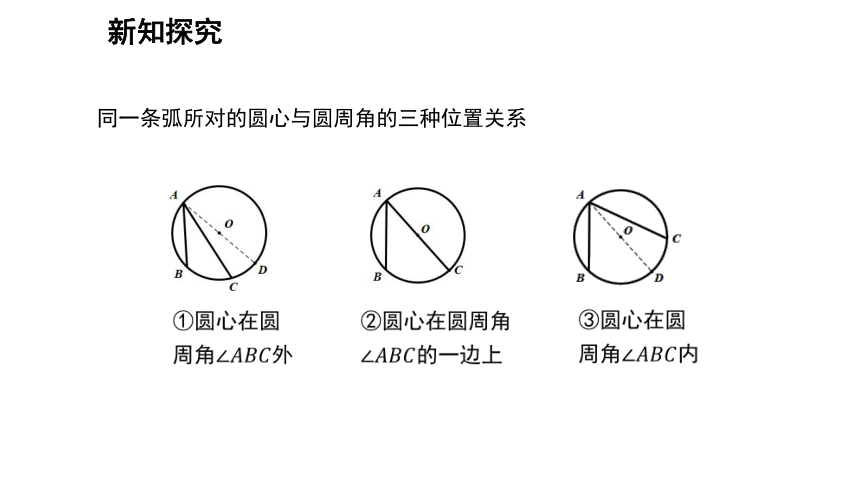
同一条弧所对的圆心与圆周角的三种位置关系
新知探究
C
分析:
新知探究
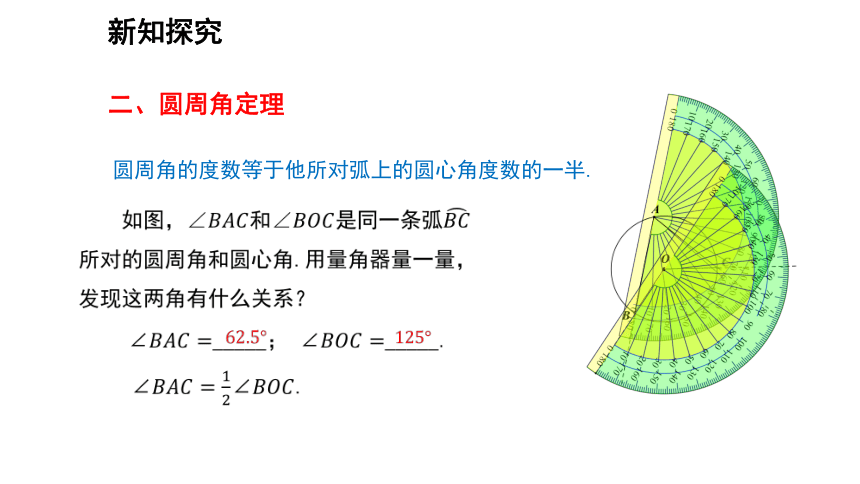
二、圆周角定理
圆周角的度数等于他所对弧上的圆心角度数的一半.
新知探究
证明:
①圆周角的一边过圆心.
新知探究
②圆心在圆周角的内部.
新知探究
③圆心在圆周角的外部.
新知探究
分析:
根据圆周角定理,得
三、圆周角定理的推论1
新知探究
在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
圆周角定理的推论
练习 如图,点A,B,C,D在☉O上,点A与点D在点B,C所在直线的同侧,∠BAC=37 ,则 ∠BOC= ,∠BDC= .
74
37
新知探究
解:
新知探究
解:
E
本课小结
一、圆周角
顶点在圆上,且角的两边与圆相交的角叫作圆周角.
二、圆周角定理
圆周角的度数等于他所对弧上的圆心角度数的一半.
三、圆周角定理的推论1
在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
课堂小测
1.判断
(1)同一个圆中等弧所对的圆周角相等; ( )
(2)相等的弦所对的圆周角也相等; ( )
(3)同弦所对的圆周角相等. ( )
√
×
×
课堂小测
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°,
则∠AOB=__________.
B
A
C
O
3.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
166°
第2章
圆
九年级数学湘教版·下册
2.2.2.1 圆周角定理及推论1
授课人:XXXX
1.理解圆周角的概念,会叙述并证明圆周角定理.
教学目标
2.能运用圆周角定理解决简单的几何问题.(重点、难点)
3.理解掌握圆周角定理的推论1,并能熟练运用.(难点)
新课导入
前面我们学习了顶点在圆心的角——圆心角,下面学习顶点在圆周上的角(如图).
新知探究
一、圆周角
顶点在圆上,且角的两边与圆相交的角叫作圆周角.
①
②
④
③
新知探究
同一条弧所对的圆心与圆周角的三种位置关系
新知探究
C
分析:
新知探究
二、圆周角定理
圆周角的度数等于他所对弧上的圆心角度数的一半.
新知探究
证明:
①圆周角的一边过圆心.
新知探究
②圆心在圆周角的内部.
新知探究
③圆心在圆周角的外部.
新知探究
分析:
根据圆周角定理,得
三、圆周角定理的推论1
新知探究
在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
圆周角定理的推论
练习 如图,点A,B,C,D在☉O上,点A与点D在点B,C所在直线的同侧,∠BAC=37 ,则 ∠BOC= ,∠BDC= .
74
37
新知探究
解:
新知探究
解:
E
本课小结
一、圆周角
顶点在圆上,且角的两边与圆相交的角叫作圆周角.
二、圆周角定理
圆周角的度数等于他所对弧上的圆心角度数的一半.
三、圆周角定理的推论1
在同圆(或等圆)中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等.
课堂小测
1.判断
(1)同一个圆中等弧所对的圆周角相等; ( )
(2)相等的弦所对的圆周角也相等; ( )
(3)同弦所对的圆周角相等. ( )
√
×
×
课堂小测
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°,
则∠AOB=__________.
B
A
C
O
3.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
166°
