2021-2022学年度湘教版九年级数学下册 2.5.2.1 圆的切线的判定 课件(共14张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版九年级数学下册 2.5.2.1 圆的切线的判定 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第2章
圆
九年级数学湘教版·下册
2.5.2.1 圆的切线的判定
授课人:XXXX
教学目标
2.会过圆上一点作圆的切线;
1.理解并掌握圆的切线的判定定理.(重点)
3.能运用圆的切线的判定定理解决问题.(难点)
新课导入
生活中我们常常看到切线的实例,那么如何判断一条直线是不是圆的切线呢?
新知探究
一、圆的切线的判定
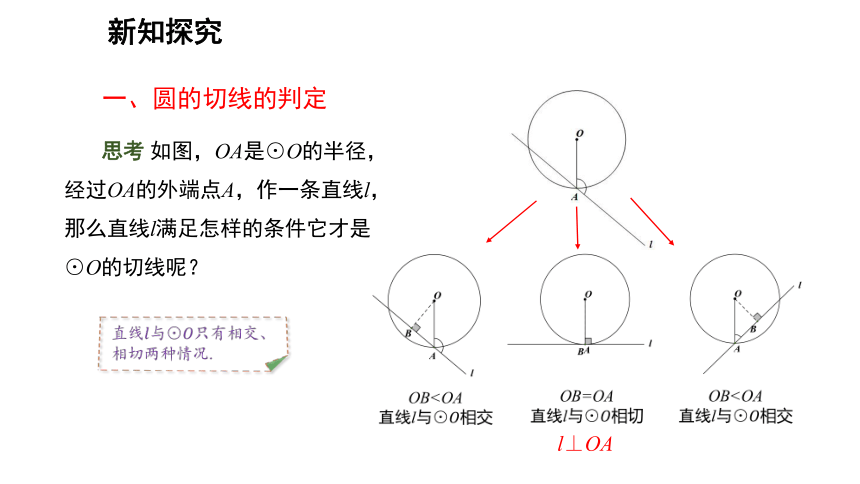
思考 如图,OA是⊙O的半径,
经过OA的外端点A,作一条直线l,
那么直线l满足怎样的条件它才是
⊙O的切线呢?
l⊥OA
新知探究
圆的切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
练习 如图,∠ABC=45°,直线AB是☉O上的直径,且AB=AC.
求证:AC是☉O的切线.
证明:
∵AB是☉O的直径,
∴ AC是☉O的切线.
新知探究
二、过圆上一点画圆的切线(用三角尺)
画法:
(1)连接OP,将三角尺的直角顶点放在
点P处,并使一直角边与半径OP重合;
(2)过点P沿着三角尺的另一条直角边画直线l,
则l就是所要画的切线.
如图,已知⊙O上一点P,用三角尺过点P画⊙O的切线.
新知探究
【例题1】如图,已知AD是⊙O的直径,直线BC经过点D,并且AB=AC. ∠BAD=∠CAD. 求证:直线BC是⊙O的切线.
∵AB=AC , ∠BAD=∠CAD,
证明:
∴AD⊥BC.
又∵OD是⊙O的半径,且BC经过点D,
∴直线BC是⊙O的切线.
新知探究
分析:
当直线与圆没有明确的公共点时,利用
“作垂直,证半径”证明圆的切线.
新知探究
证明:
本课小结
圆的切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
证切线的方法
(1) 直线与圆明确交点,(连半径),证垂直;(例题1)
(2) 直线与圆没有明确交点,作垂直,证半径.(例题2)
课堂小测
1.判断下列命题是否正确.
⑴ 经过半径外端的直线是圆的切线. ( )
⑵ 垂直于半径的直线是圆的切线. ( )
⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线.( )
⑷ 和圆只有一个公共点的直线是圆的切线. ( )
⑸ 过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
课堂小测
2.如图所示,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 .
相切
课堂小测
3.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.
O
A
B
C
E
P
∴PE为⊙O的切线.
证明:
连接OP.
∵AB=AC,
∴∠B=∠C.
∵OB=OP,
∴∠B=∠OPB.
∴∠OPB=∠C.
∴OP∥AC.
∵PE⊥AC,
∴PE⊥OP.
第2章
圆
九年级数学湘教版·下册
2.5.2.1 圆的切线的判定
授课人:XXXX
教学目标
2.会过圆上一点作圆的切线;
1.理解并掌握圆的切线的判定定理.(重点)
3.能运用圆的切线的判定定理解决问题.(难点)
新课导入
生活中我们常常看到切线的实例,那么如何判断一条直线是不是圆的切线呢?
新知探究
一、圆的切线的判定
思考 如图,OA是⊙O的半径,
经过OA的外端点A,作一条直线l,
那么直线l满足怎样的条件它才是
⊙O的切线呢?
l⊥OA
新知探究
圆的切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
练习 如图,∠ABC=45°,直线AB是☉O上的直径,且AB=AC.
求证:AC是☉O的切线.
证明:
∵AB是☉O的直径,
∴ AC是☉O的切线.
新知探究
二、过圆上一点画圆的切线(用三角尺)
画法:
(1)连接OP,将三角尺的直角顶点放在
点P处,并使一直角边与半径OP重合;
(2)过点P沿着三角尺的另一条直角边画直线l,
则l就是所要画的切线.
如图,已知⊙O上一点P,用三角尺过点P画⊙O的切线.
新知探究
【例题1】如图,已知AD是⊙O的直径,直线BC经过点D,并且AB=AC. ∠BAD=∠CAD. 求证:直线BC是⊙O的切线.
∵AB=AC , ∠BAD=∠CAD,
证明:
∴AD⊥BC.
又∵OD是⊙O的半径,且BC经过点D,
∴直线BC是⊙O的切线.
新知探究
分析:
当直线与圆没有明确的公共点时,利用
“作垂直,证半径”证明圆的切线.
新知探究
证明:
本课小结
圆的切线的判定定理
经过半径的外端并且垂直于这条半径的直线是圆的切线.
证切线的方法
(1) 直线与圆明确交点,(连半径),证垂直;(例题1)
(2) 直线与圆没有明确交点,作垂直,证半径.(例题2)
课堂小测
1.判断下列命题是否正确.
⑴ 经过半径外端的直线是圆的切线. ( )
⑵ 垂直于半径的直线是圆的切线. ( )
⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线.( )
⑷ 和圆只有一个公共点的直线是圆的切线. ( )
⑸ 过直径一端点且垂直于直径的直线是圆的切线. ( )
×
×
√
√
√
课堂小测
2.如图所示,A是☉O上一点,且AO=5,PO=13,AP=12,则PA与☉O的位置关系是 .
相切
课堂小测
3.如图,△ABC中,AB=AC,以AB为直径的⊙O交边BC于P, PE⊥AC于E.
求证:PE是⊙O的切线.
O
A
B
C
E
P
∴PE为⊙O的切线.
证明:
连接OP.
∵AB=AC,
∴∠B=∠C.
∵OB=OP,
∴∠B=∠OPB.
∴∠OPB=∠C.
∴OP∥AC.
∵PE⊥AC,
∴PE⊥OP.
