2021-2022学年度湘教版九年级数学下册 2.5.3 切线长定理 课件(共14张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版九年级数学下册 2.5.3 切线长定理 课件(共14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 16:16:36 | ||
图片预览





文档简介
(共14张PPT)
第2章
圆
九年级数学湘教版·下册
2.5.3 切线长定理
授课人:XXXX
教学目标
1.理解并掌握切线长的定义及切线长定理.(重点)
2.会运用切线长定理进行计算与证明.(难点)
新课导入
我们学习了用三角尺过圆上一点画圆的切线,那么如何用三角尺过圆外一点画圆的切线呢?
新知探究
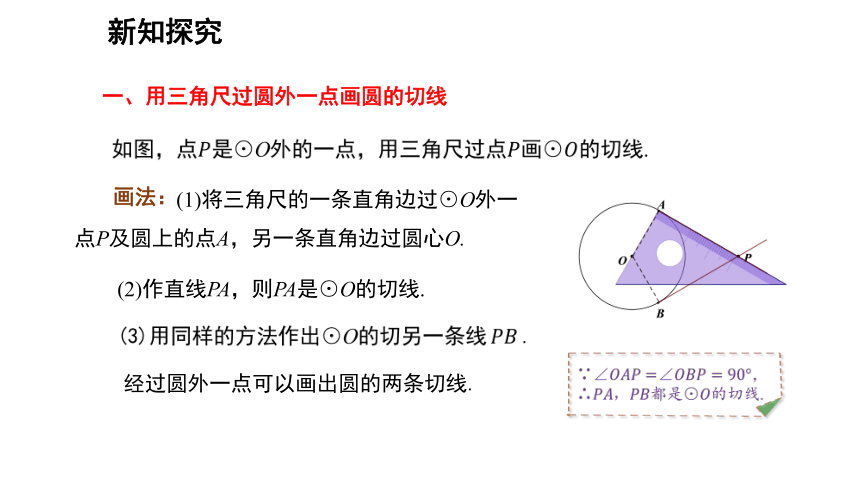
一、用三角尺过圆外一点画圆的切线
(1)将三角尺的一条直角边过⊙O外一点P及圆上的点A,另一条直角边过圆心O.
画法:
(2)作直线PA,则PA是⊙O的切线.
经过圆外一点可以画出圆的两条切线.
新知探究
二、切线长定理
②切线长是线段的长度,它是一个度量值.
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
切线长与切线的区别:
①切线是直线,它是几何图形.
新知探究
切线长定理
过圆外一点所画的圆的两条切线长相等,
圆心和这点的连线平分两条切线的夹角.
新知探究
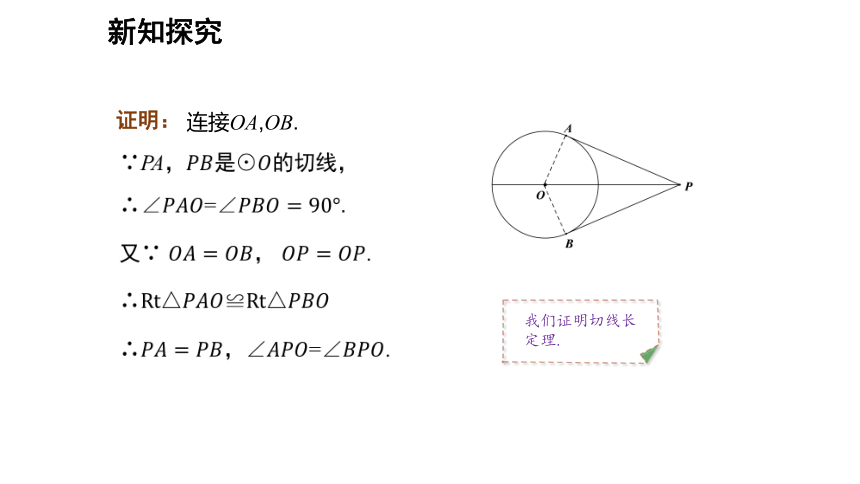
证明:
我们证明切线长定理.
连接OA,OB.
新知探究
证明:
构造直径对的圆周角是常用的辅助线.
新知探究
连接过切点的半径是常用的辅助线.
证明:
新知探究
【例题3】已知:如图,四边形ABCD的边AB,BC,CD,DA与⊙O分别相切于点E,F,G,H.求证:AB+CD=AD+BC.
出现圆外一点到圆的切线图形,就要联想到切线长定理.
证明:
∴ AE=AH,BE=BF,CG=CF,DG=DH.
∴ AE+BE+CG+DG=AH+BF+CF+DH.
∴AB+CD=AD+BC.
本课小结
一、圆的切线长
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
二、切线长定理
过圆外一点所作的圆的两条切线长相等,圆心和这点的连线平分两条切线的夹角.
课堂小测
5
6
1.PA,PB是☉O的两条切线,A,B是切点,OA=3.
(1)若AP=4,则OP= ;
(2)若∠BPA=60 °,则OP= .
课堂小测
证明:
连接OD,
∵AC切⊙O点D,∴OD⊥AC,
在Rt△OCD和Rt△OCB中,OD=OB ,OC=OC,
∴Rt△ODC≌Rt△OBC.
∴∠DOC=∠BOC.
∵OD=OE,
∴∠ODE=∠OED,
∵∠DOB=∠ODE+∠OED,
∴DE∥OC.
∴∠BOC=∠OED,
第2章
圆
九年级数学湘教版·下册
2.5.3 切线长定理
授课人:XXXX
教学目标
1.理解并掌握切线长的定义及切线长定理.(重点)
2.会运用切线长定理进行计算与证明.(难点)
新课导入
我们学习了用三角尺过圆上一点画圆的切线,那么如何用三角尺过圆外一点画圆的切线呢?
新知探究
一、用三角尺过圆外一点画圆的切线
(1)将三角尺的一条直角边过⊙O外一点P及圆上的点A,另一条直角边过圆心O.
画法:
(2)作直线PA,则PA是⊙O的切线.
经过圆外一点可以画出圆的两条切线.
新知探究
二、切线长定理
②切线长是线段的长度,它是一个度量值.
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
切线长与切线的区别:
①切线是直线,它是几何图形.
新知探究
切线长定理
过圆外一点所画的圆的两条切线长相等,
圆心和这点的连线平分两条切线的夹角.
新知探究
证明:
我们证明切线长定理.
连接OA,OB.
新知探究
证明:
构造直径对的圆周角是常用的辅助线.
新知探究
连接过切点的半径是常用的辅助线.
证明:
新知探究
【例题3】已知:如图,四边形ABCD的边AB,BC,CD,DA与⊙O分别相切于点E,F,G,H.求证:AB+CD=AD+BC.
出现圆外一点到圆的切线图形,就要联想到切线长定理.
证明:
∴ AE=AH,BE=BF,CG=CF,DG=DH.
∴ AE+BE+CG+DG=AH+BF+CF+DH.
∴AB+CD=AD+BC.
本课小结
一、圆的切线长
经过圆外一点作圆的切线,这点和切点之间的线段的长,叫作这点到圆的切线长.
二、切线长定理
过圆外一点所作的圆的两条切线长相等,圆心和这点的连线平分两条切线的夹角.
课堂小测
5
6
1.PA,PB是☉O的两条切线,A,B是切点,OA=3.
(1)若AP=4,则OP= ;
(2)若∠BPA=60 °,则OP= .
课堂小测
证明:
连接OD,
∵AC切⊙O点D,∴OD⊥AC,
在Rt△OCD和Rt△OCB中,OD=OB ,OC=OC,
∴Rt△ODC≌Rt△OBC.
∴∠DOC=∠BOC.
∵OD=OE,
∴∠ODE=∠OED,
∵∠DOB=∠ODE+∠OED,
∴DE∥OC.
∴∠BOC=∠OED,
