2021-2022学年度湘教版九年级数学下册 2.5.4 三角形的内切圆 课件(共13张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版九年级数学下册 2.5.4 三角形的内切圆 课件(共13张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 16:17:28 | ||
图片预览




文档简介
(共13张PPT)
第2章
圆
九年级数学湘教版·下册
2.5.4 三角形的内切圆
授课人:XXXX
教学目标
1.掌握三角形内切圆的尺规作图方法;
2.掌握三角形内切圆的概念、三角形内心的性质,并能运用解决问题.
(重点、难点)
新课导入
我们知道三角形的外接圆经过三角形的三个顶点,那么有没有一个圆与三角形的三条边都相切呢?
新知探究
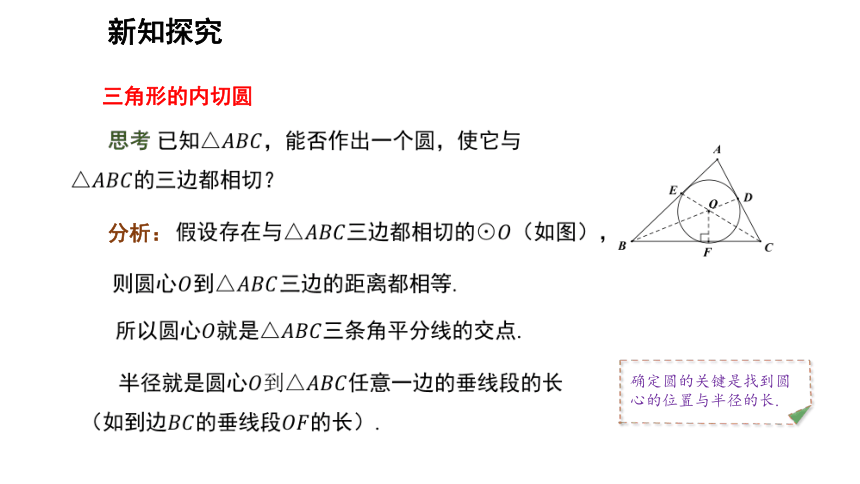
三角形的内切圆
分析:
确定圆的关键是找到圆心的位置与半径的长.
新知探究
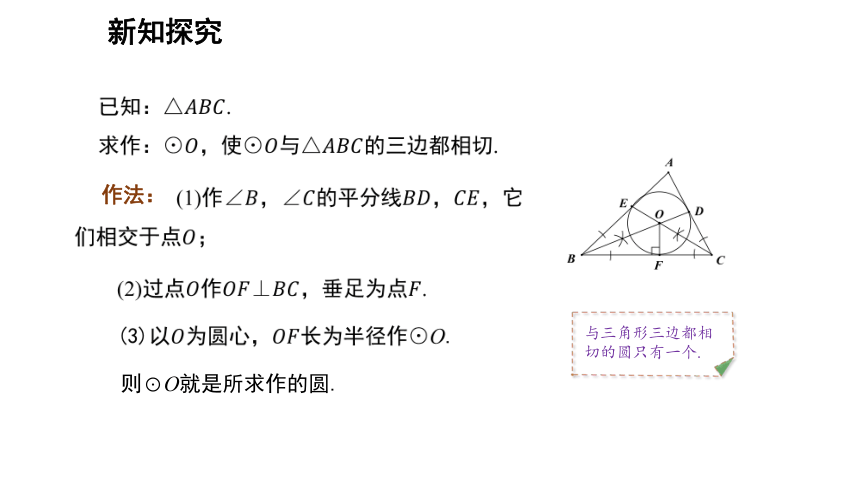
作法:
则⊙O就是所求作的圆.
与三角形三边都相切的圆只有一个.
新知探究
三角形内心的性质:三角形的内心到三角形三边的距离都相等.
与三角形各边都相切的圆叫作三角形的内切圆,这个三角形叫作圆的外切三角形.
三角形内切圆的圆心叫作三角形的内心.
三角形的内心是这个三角形的三条角平分线的交点.
新知探究
解:
新知探究
连接过切点的半径是常用的辅助线.
证明:
新知探究
抓住三角形内心与平移这两个关键条件.
解:
本课小结
三角形的内切圆
三角形内心的性质:三角形的内心到三角形三边的距离相等.
与三角形各边都相切的圆叫作三角形的内切圆,这个三角形叫作圆的外切三角形..
三角形内切圆的圆心叫作三角形的内心.
三角形的内心是这个三角形的三条角平分线的交点.
课堂小测
1.如图,△ABC中,∠ B=43°,∠C=61 °,点I是△ABC的内心,求
∠ BIC的度数.
连接IB,IC.
∵点I是△ABC的内心,
∴IB,IC分别是∠ B,∠C的平分线,
在△IBC中,
解:
课堂小测
2.如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:BD=ID.
证明:
∴BD=ID.
连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
第2章
圆
九年级数学湘教版·下册
2.5.4 三角形的内切圆
授课人:XXXX
教学目标
1.掌握三角形内切圆的尺规作图方法;
2.掌握三角形内切圆的概念、三角形内心的性质,并能运用解决问题.
(重点、难点)
新课导入
我们知道三角形的外接圆经过三角形的三个顶点,那么有没有一个圆与三角形的三条边都相切呢?
新知探究
三角形的内切圆
分析:
确定圆的关键是找到圆心的位置与半径的长.
新知探究
作法:
则⊙O就是所求作的圆.
与三角形三边都相切的圆只有一个.
新知探究
三角形内心的性质:三角形的内心到三角形三边的距离都相等.
与三角形各边都相切的圆叫作三角形的内切圆,这个三角形叫作圆的外切三角形.
三角形内切圆的圆心叫作三角形的内心.
三角形的内心是这个三角形的三条角平分线的交点.
新知探究
解:
新知探究
连接过切点的半径是常用的辅助线.
证明:
新知探究
抓住三角形内心与平移这两个关键条件.
解:
本课小结
三角形的内切圆
三角形内心的性质:三角形的内心到三角形三边的距离相等.
与三角形各边都相切的圆叫作三角形的内切圆,这个三角形叫作圆的外切三角形..
三角形内切圆的圆心叫作三角形的内心.
三角形的内心是这个三角形的三条角平分线的交点.
课堂小测
1.如图,△ABC中,∠ B=43°,∠C=61 °,点I是△ABC的内心,求
∠ BIC的度数.
连接IB,IC.
∵点I是△ABC的内心,
∴IB,IC分别是∠ B,∠C的平分线,
在△IBC中,
解:
课堂小测
2.如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.
求证:BD=ID.
证明:
∴BD=ID.
连接BI.
∵I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD,
