2021-2022学年度湘教版九年级数学下册 4.3用频率估计概率 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年度湘教版九年级数学下册 4.3用频率估计概率 课件(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
第4章
概率
九年级数学湘教版·下册
4.3 用频率估计概率
授课人:XXXX
教学目标
2.理解试验次数较大时试验频率趋于稳定这一规律;(重点)
3.结合具体问题会用频率估计概率.(重点、难点)
1.通过计算和试验理解概率与频率之间的关系;
新课导入
前面我们学习了用概率公式求等可能事件的概率. 而通过大量的重复试验既可以估计出等可能事件概率,也可以估计出结果非有限个或非等可能事件的概率.
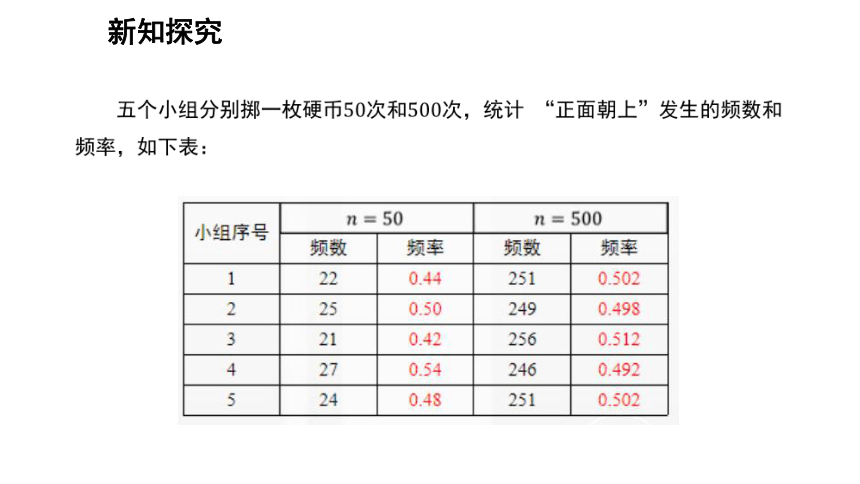
新知探究
一、概率是频率的稳定值
新知探究
新知探究
新知探究
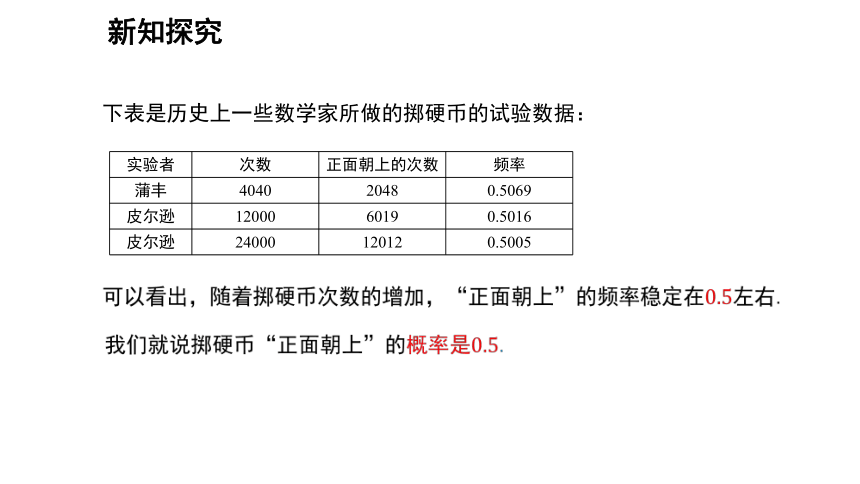
下表是历史上一些数学家所做的掷硬币的试验数据:
实验者 次数 正面朝上的次数 频率
蒲丰 4040 2048 0.5069
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
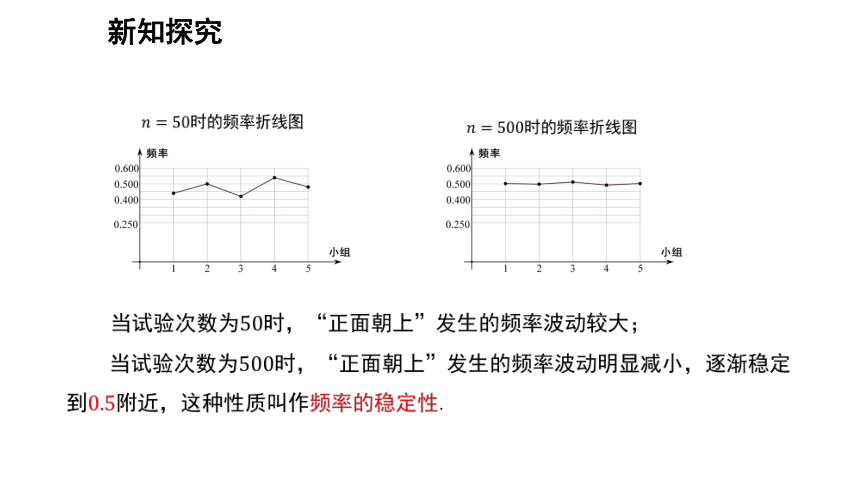
新知探究
在随机事件中,每次试验的结果都是随机的,无法预测,但随着试验次数的增加,事件的频率逐渐稳定到某一个数值附近,这种性质叫作频率的稳定性.
对于掷硬币试验,它的所有可能结果只有两个,而且出现两种可能结果的可能性相等,可以用前面学习的概率计算公式求出概率.
新知探究
二、用频率估计概率
对于一般的随机事件,当试验所有可能的结果不是有限个,或者各种可能结果发生的可能性不相等时,就不能用公式求概率了,而是通过大量的重复试验,用频率估计概率.
新知探究
试验2 在一块平整地板上抛掷一个矿泉水瓶盖,瓶盖落地后有两种可能情况“开口朝上”和“开口不朝上”.
由于瓶盖质地不均匀(头重脚轻),上下不对称,“开口朝上”和“开口不朝上”的可能性是不一样的,那么出现哪种情况的可能性大一些呢
通过大量重复试验来解决这个问题.
新知探究
将全班同学分成6组,每组同学依次抛掷瓶盖80次,观察瓶盖着地时的情况,并根据全班试验结果得到了下表:
累计抛掷次数 80 160 240 320 400 480
“开口朝上”的次数 50 84 135 177 227 271
“开口朝上”的频率 0.6250 0.5250 0.5625 0.5531 0.5675 0.5646
“开口朝上”频率折线图
新知探究
“开口朝上”频率折线图
新知探究
大量重复试验能够呈现事件发生可能性大小的规律——概率. 我们可以通过多次重复试验,利用频率的稳定性去估计概率.而试验次数越大,得到概率较精确的估计值的可能性越大.
频率和概率都是随机事件可能性大小的定量的刻画,但频率与试验次数及具体的试验有关,因此,频率具有随机性;
而概率是刻画随机事件发生可能性大小的数值,是一个固定的量,不具有随机性.
新知探究
【例题1】瓷砖生产过程中的“合格品”是一个随机事件,这个事件的概率称为“合格品率”.由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计值.
某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
(1)计算上表中合格品的各频率(精确到0.001);
(2)估计这种瓷砖的合格品率(精确到0.01);
(3)若该工厂本月生产该型号瓷砖500000块,试估计合格品数.
新知探究
解:
(1)逐项计算,填表如下:
本课小结
一、概率是频率的稳定值
在随机事件中,每次试验的结果都是随机的,无法预测,但随着试验次数的增加,事件的频率逐渐稳定到某一个数值附近,这种性质叫作频率的稳定性.
本课小结
二、用频率估计概率
我们可以通过多次重复试验,利用频率的稳定性去估计概率. 而试验次数越大,得到概率较精确的估计值的可能性越大.
课堂小测
1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼 尾,鲢鱼 尾.
310
270
课堂小测
分析:
12
第4章
概率
九年级数学湘教版·下册
4.3 用频率估计概率
授课人:XXXX
教学目标
2.理解试验次数较大时试验频率趋于稳定这一规律;(重点)
3.结合具体问题会用频率估计概率.(重点、难点)
1.通过计算和试验理解概率与频率之间的关系;
新课导入
前面我们学习了用概率公式求等可能事件的概率. 而通过大量的重复试验既可以估计出等可能事件概率,也可以估计出结果非有限个或非等可能事件的概率.
新知探究
一、概率是频率的稳定值
新知探究
新知探究
新知探究
下表是历史上一些数学家所做的掷硬币的试验数据:
实验者 次数 正面朝上的次数 频率
蒲丰 4040 2048 0.5069
皮尔逊 12000 6019 0.5016
皮尔逊 24000 12012 0.5005
新知探究
在随机事件中,每次试验的结果都是随机的,无法预测,但随着试验次数的增加,事件的频率逐渐稳定到某一个数值附近,这种性质叫作频率的稳定性.
对于掷硬币试验,它的所有可能结果只有两个,而且出现两种可能结果的可能性相等,可以用前面学习的概率计算公式求出概率.
新知探究
二、用频率估计概率
对于一般的随机事件,当试验所有可能的结果不是有限个,或者各种可能结果发生的可能性不相等时,就不能用公式求概率了,而是通过大量的重复试验,用频率估计概率.
新知探究
试验2 在一块平整地板上抛掷一个矿泉水瓶盖,瓶盖落地后有两种可能情况“开口朝上”和“开口不朝上”.
由于瓶盖质地不均匀(头重脚轻),上下不对称,“开口朝上”和“开口不朝上”的可能性是不一样的,那么出现哪种情况的可能性大一些呢
通过大量重复试验来解决这个问题.
新知探究
将全班同学分成6组,每组同学依次抛掷瓶盖80次,观察瓶盖着地时的情况,并根据全班试验结果得到了下表:
累计抛掷次数 80 160 240 320 400 480
“开口朝上”的次数 50 84 135 177 227 271
“开口朝上”的频率 0.6250 0.5250 0.5625 0.5531 0.5675 0.5646
“开口朝上”频率折线图
新知探究
“开口朝上”频率折线图
新知探究
大量重复试验能够呈现事件发生可能性大小的规律——概率. 我们可以通过多次重复试验,利用频率的稳定性去估计概率.而试验次数越大,得到概率较精确的估计值的可能性越大.
频率和概率都是随机事件可能性大小的定量的刻画,但频率与试验次数及具体的试验有关,因此,频率具有随机性;
而概率是刻画随机事件发生可能性大小的数值,是一个固定的量,不具有随机性.
新知探究
【例题1】瓷砖生产过程中的“合格品”是一个随机事件,这个事件的概率称为“合格品率”.由于烧制结果不是等可能的,我们常用“合格品”的频率作为“合格品率”的估计值.
某瓷砖厂对最近出炉的一大批某型号瓷砖进行质量抽检,结果如下:
(1)计算上表中合格品的各频率(精确到0.001);
(2)估计这种瓷砖的合格品率(精确到0.01);
(3)若该工厂本月生产该型号瓷砖500000块,试估计合格品数.
新知探究
解:
(1)逐项计算,填表如下:
本课小结
一、概率是频率的稳定值
在随机事件中,每次试验的结果都是随机的,无法预测,但随着试验次数的增加,事件的频率逐渐稳定到某一个数值附近,这种性质叫作频率的稳定性.
本课小结
二、用频率估计概率
我们可以通过多次重复试验,利用频率的稳定性去估计概率. 而试验次数越大,得到概率较精确的估计值的可能性越大.
课堂小测
1.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾,一渔民通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率是31%和42%,则这个水塘里有鲤鱼 尾,鲢鱼 尾.
310
270
课堂小测
分析:
12
