人教A版高中数学必修第一册课件《 函数及其表示方法》(共22张ppt)
文档属性
| 名称 | 人教A版高中数学必修第一册课件《 函数及其表示方法》(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-22 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
3.1.1函数及其表示方法(第一课时)
【自主预习】
1.变量:在一个变化过程中,数值发生变化的量叫变量.
2.函数的传统定义:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就称y是x的函数.
3.初中实际上是用变量的观点和解析式来描述函数的。
4.初中学过哪几种函数?正比例函数、反比例函数、一次函数、二次函数。
第三章 函 数
[数学文化]——了解函数的演变过程
1.早期函数概念——几何观念下的函数
1673年,德国数学家莱布尼茨首次使用“function”(函数)表示“幂”.用这个词表示与曲线上的点有关的线段长度,并使用这个词表示变量之间的依赖关系。
2.十八世纪函数概念——代数观念下的函数
1734年,瑞士数学家欧拉首次使用字母f表示函数,在《微积分》中将函数定义为“如果某些变量,以一种方式依赖于另一些变量,我们将前面的变量称为后面变量的函数.”
3.十九世纪函数概念——对应关系下的函数
1837年德国数学家狄利克雷提出:“如果对于x的每一个值,y总有一个完全确定的值与之对应,则y是x的函数.”
1851年德国数学家黎曼给出的函数定义是:假定z是一个变量,它可以依次取所有可能的实数集,如果对于它的每一个值,都有未知量w的唯一确定的一个值与之对应,则w称为z的一个函数,
4. 20世纪函数概念-----关系说下的函数
1939年,法国布尔巴基学派定义为,设F是定义在集合X和Y上的一个二元关系,如果对于每一个
称这个关系为函数.
【教学目标 】
1.在初中用变量之间的依赖关系描述函数的基础上,用集合语言和对应关系刻画函数,建立完整的函数概念,培养数学抽象的核心素养;
2.体会集合语言和对应关系在刻画函数概念中的作用;
3.了解构成函数的要素及同一个函数的概念,能求简单函数的定义域和值域,提升数学运算的核心素养.
教学重点:函数概念的抽象与认识
教学难点:用对应关系刻画函数概念,抽象符号的引入.
情境(1) 国家统计局的课题组公布,如果将2005年中国创新指数记为100,近些年来中国创新指数的情况如下表所示,以 y表示年度值, i 表示中国创新指数的取值,
问题1.这里 i是y 的函数吗 如果是,这个函数用数学符号可以怎样表示
创设情境, 引入概念.
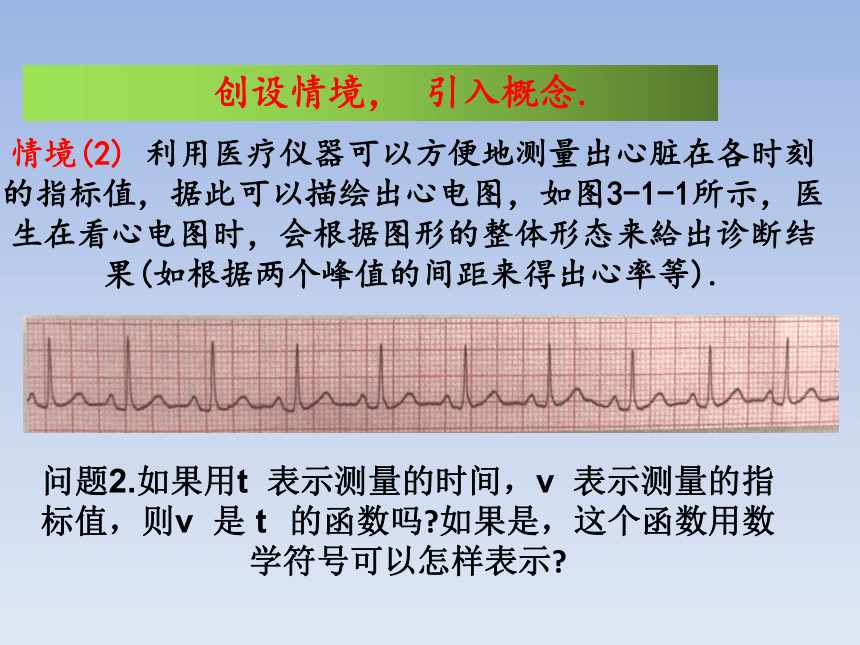
情境(2) 利用医疗仪器可以方便地测量出心脏在各时刻的指标值,据此可以描绘出心电图,如图3-1-1所示,医生在看心电图时,会根据图形的整体形态来給出诊断结果(如根据两个峰值的间距来得出心率等).
问题2.如果用t 表示测量的时间,v 表示测量的指标值,则v 是 t 的函数吗 如果是,这个函数用数学符号可以怎样表示
创设情境, 引入概念.
函数的定义:一般地,给定两个非空实数集A与B,以及对应关系f,如果对于集合A中的每一个实数x,在集合B中都有唯一确定的实数y与x对应,则称f为定义在集合A上的一个函数,记作y=f(x),x∈A.其中x称为自变量,自变量取值的范围(即数集A)称为这个函数的定义域.y称为因变量,所有函数值组成的集合{y∈B|y=f(x),x∈A},称为函数的值域。
[环节一] 抽象概念,剖析概念.
[问题3] 函数的这种定义强调的是什么?
[问题4] 如何判断一个对应关系是不是函数,要从哪些方面判断?
[问题5]函数的定义中,定义域和集合A有什么关系?值域和集合B有什么关系?
[问题6]函数定义中, y=f(x)表示什么?f(x)与f(1)有什么区别?
[问题7]自变量与因变量用什么字母表示有关系吗?
[问题8]在函数的概念中,如果函数y=f(x)的定义域与对应关系确定,那么函数的值域确定吗?
[问题9]如果两个函数是同一函数,需要满足什么条件?
1.函数的值域被定义域和对应关系完全确定,所以确定一个函数只需要知道函数的定义域和对应关系。
2.同一函数:如果两个函数表达式表示的函数定义域相同,对应关系也相同(即对自变量的每一个值,两个函数表达式得到的函数值都相等),则称这两个函数表达式表示的就是同一个函数。
问题11.表示函数时,函数的定义域可以不写吗?若不写,则函数的定义域是什么?
3.函数的定义域就是使函数有意义的所有实数组成的集合
[环节一] 抽象概念,剖析概念.
[环节二] 应用概念,学以致用.
例 1 (1)判断下列“箭头图”表示的对应关系 f: A→B 是否为函数.
思考:判断一个对应f: A→B是否是函数的方法
满足①A、B非空数集②A中元素的任意性③B中元素的唯一性
由例(1)可知定义域=A,值域是B的子集
思考:如何判断一个图像是否是函数的图像呢?
取垂直于的x轴直线在定义域内平行移动,与图形只有一个交点则是函数图像,否则不是
相关概念的考察.
[环节二] 应用概念,学以致用.
(3)(多选)已知下列四组函数表示同一函数的是( )
思考: 同一函数的判定方法 .
定义域相同,对应关系也相同的函数是同一函数,二者中有一个不同,则不是同一函数 .
[环节二] 应用概念,学以致用.
思考:函数的定义域不写时,是如何约定的?
函数的定义域就是使函数有意义的所有实数组成的集合.
例2 求下列函数的定义域:
;
函数定义域的求法
小结:对于一个确定的函数关系式,我们通常从哪些方面考虑求函数的定义域?
(1)整式:
(2)分式:
(3)二次根式(偶次根式):
(4)零次幂:
(5)若函数由几部分构成:
(6)实际问题:
分母不为0
被开方数≥0
全体实数
幂底数不为0
定义域是使各部分式子都有意义的集合的交集
除考虑解析式本身有意义外,还应考虑实际问题有意义
[环节二] 应用概念,学以致用.
跟踪训练1. 求下列函数的定义域.
[环节二] 应用概念,学以致用.
[环节二] 应用概念,学以致用.
例3
函数值与函数值域
思考:函数的值域由什么确定?.
函数的值域由定义域和对应关系确定,故求值域要考虑这两方面
跟踪训练2.已知函数f(x)= 的值域为S,
试判断 是否是S中的元素.
[环节二] 应用概念,学以致用.
课堂小结,总结升华.通过本节课的学习,你有什么收获?
当堂检测
1.(多选)下列说法中,正确的是 ( )
A.在函数y=f(x)中,对于不同的x,y也不同.
B.函数f(x)=x2-x与g(t)=t2-t不是同一函数
C.定义域和对应法则确定后,函数值域也就确定
D.若函数的定义域只有一个元素,则值域也只有一个元素
2.若A={x|0≤x≤2},B={y|1≤y≤2},下列图形中能表示以A为定义域,B为值域的函数的是( )
CD
B
{x|x≥-5且x≠2}
课后作业,巩固新知.
阅读课本,结合学案,进行知识整理,形成系统.
课本93页94页练习A1、2、3、4、5,
练习B 1、2、4、5;
预习函数的表示方法。
谢谢大家!
3.1.1函数及其表示方法(第一课时)
【自主预习】
1.变量:在一个变化过程中,数值发生变化的量叫变量.
2.函数的传统定义:在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么就称y是x的函数.
3.初中实际上是用变量的观点和解析式来描述函数的。
4.初中学过哪几种函数?正比例函数、反比例函数、一次函数、二次函数。
第三章 函 数
[数学文化]——了解函数的演变过程
1.早期函数概念——几何观念下的函数
1673年,德国数学家莱布尼茨首次使用“function”(函数)表示“幂”.用这个词表示与曲线上的点有关的线段长度,并使用这个词表示变量之间的依赖关系。
2.十八世纪函数概念——代数观念下的函数
1734年,瑞士数学家欧拉首次使用字母f表示函数,在《微积分》中将函数定义为“如果某些变量,以一种方式依赖于另一些变量,我们将前面的变量称为后面变量的函数.”
3.十九世纪函数概念——对应关系下的函数
1837年德国数学家狄利克雷提出:“如果对于x的每一个值,y总有一个完全确定的值与之对应,则y是x的函数.”
1851年德国数学家黎曼给出的函数定义是:假定z是一个变量,它可以依次取所有可能的实数集,如果对于它的每一个值,都有未知量w的唯一确定的一个值与之对应,则w称为z的一个函数,
4. 20世纪函数概念-----关系说下的函数
1939年,法国布尔巴基学派定义为,设F是定义在集合X和Y上的一个二元关系,如果对于每一个
称这个关系为函数.
【教学目标 】
1.在初中用变量之间的依赖关系描述函数的基础上,用集合语言和对应关系刻画函数,建立完整的函数概念,培养数学抽象的核心素养;
2.体会集合语言和对应关系在刻画函数概念中的作用;
3.了解构成函数的要素及同一个函数的概念,能求简单函数的定义域和值域,提升数学运算的核心素养.
教学重点:函数概念的抽象与认识
教学难点:用对应关系刻画函数概念,抽象符号的引入.
情境(1) 国家统计局的课题组公布,如果将2005年中国创新指数记为100,近些年来中国创新指数的情况如下表所示,以 y表示年度值, i 表示中国创新指数的取值,
问题1.这里 i是y 的函数吗 如果是,这个函数用数学符号可以怎样表示
创设情境, 引入概念.
情境(2) 利用医疗仪器可以方便地测量出心脏在各时刻的指标值,据此可以描绘出心电图,如图3-1-1所示,医生在看心电图时,会根据图形的整体形态来給出诊断结果(如根据两个峰值的间距来得出心率等).
问题2.如果用t 表示测量的时间,v 表示测量的指标值,则v 是 t 的函数吗 如果是,这个函数用数学符号可以怎样表示
创设情境, 引入概念.
函数的定义:一般地,给定两个非空实数集A与B,以及对应关系f,如果对于集合A中的每一个实数x,在集合B中都有唯一确定的实数y与x对应,则称f为定义在集合A上的一个函数,记作y=f(x),x∈A.其中x称为自变量,自变量取值的范围(即数集A)称为这个函数的定义域.y称为因变量,所有函数值组成的集合{y∈B|y=f(x),x∈A},称为函数的值域。
[环节一] 抽象概念,剖析概念.
[问题3] 函数的这种定义强调的是什么?
[问题4] 如何判断一个对应关系是不是函数,要从哪些方面判断?
[问题5]函数的定义中,定义域和集合A有什么关系?值域和集合B有什么关系?
[问题6]函数定义中, y=f(x)表示什么?f(x)与f(1)有什么区别?
[问题7]自变量与因变量用什么字母表示有关系吗?
[问题8]在函数的概念中,如果函数y=f(x)的定义域与对应关系确定,那么函数的值域确定吗?
[问题9]如果两个函数是同一函数,需要满足什么条件?
1.函数的值域被定义域和对应关系完全确定,所以确定一个函数只需要知道函数的定义域和对应关系。
2.同一函数:如果两个函数表达式表示的函数定义域相同,对应关系也相同(即对自变量的每一个值,两个函数表达式得到的函数值都相等),则称这两个函数表达式表示的就是同一个函数。
问题11.表示函数时,函数的定义域可以不写吗?若不写,则函数的定义域是什么?
3.函数的定义域就是使函数有意义的所有实数组成的集合
[环节一] 抽象概念,剖析概念.
[环节二] 应用概念,学以致用.
例 1 (1)判断下列“箭头图”表示的对应关系 f: A→B 是否为函数.
思考:判断一个对应f: A→B是否是函数的方法
满足①A、B非空数集②A中元素的任意性③B中元素的唯一性
由例(1)可知定义域=A,值域是B的子集
思考:如何判断一个图像是否是函数的图像呢?
取垂直于的x轴直线在定义域内平行移动,与图形只有一个交点则是函数图像,否则不是
相关概念的考察.
[环节二] 应用概念,学以致用.
(3)(多选)已知下列四组函数表示同一函数的是( )
思考: 同一函数的判定方法 .
定义域相同,对应关系也相同的函数是同一函数,二者中有一个不同,则不是同一函数 .
[环节二] 应用概念,学以致用.
思考:函数的定义域不写时,是如何约定的?
函数的定义域就是使函数有意义的所有实数组成的集合.
例2 求下列函数的定义域:
;
函数定义域的求法
小结:对于一个确定的函数关系式,我们通常从哪些方面考虑求函数的定义域?
(1)整式:
(2)分式:
(3)二次根式(偶次根式):
(4)零次幂:
(5)若函数由几部分构成:
(6)实际问题:
分母不为0
被开方数≥0
全体实数
幂底数不为0
定义域是使各部分式子都有意义的集合的交集
除考虑解析式本身有意义外,还应考虑实际问题有意义
[环节二] 应用概念,学以致用.
跟踪训练1. 求下列函数的定义域.
[环节二] 应用概念,学以致用.
[环节二] 应用概念,学以致用.
例3
函数值与函数值域
思考:函数的值域由什么确定?.
函数的值域由定义域和对应关系确定,故求值域要考虑这两方面
跟踪训练2.已知函数f(x)= 的值域为S,
试判断 是否是S中的元素.
[环节二] 应用概念,学以致用.
课堂小结,总结升华.通过本节课的学习,你有什么收获?
当堂检测
1.(多选)下列说法中,正确的是 ( )
A.在函数y=f(x)中,对于不同的x,y也不同.
B.函数f(x)=x2-x与g(t)=t2-t不是同一函数
C.定义域和对应法则确定后,函数值域也就确定
D.若函数的定义域只有一个元素,则值域也只有一个元素
2.若A={x|0≤x≤2},B={y|1≤y≤2},下列图形中能表示以A为定义域,B为值域的函数的是( )
CD
B
{x|x≥-5且x≠2}
课后作业,巩固新知.
阅读课本,结合学案,进行知识整理,形成系统.
课本93页94页练习A1、2、3、4、5,
练习B 1、2、4、5;
预习函数的表示方法。
谢谢大家!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
