北师大版数学八年级上册 1.1.2 勾股定理的验证及其简单应用 同步课件 (共16张PPT)
文档属性
| 名称 | 北师大版数学八年级上册 1.1.2 勾股定理的验证及其简单应用 同步课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 869.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
1.1 第2课时勾股定理的验证及其简单应用
第一章 勾股定理
知识回顾
勾股定理
在Rt△ABC 中,若直角边长分别是a,b,斜边长是c,
则:
这个定理叫做:勾股定理
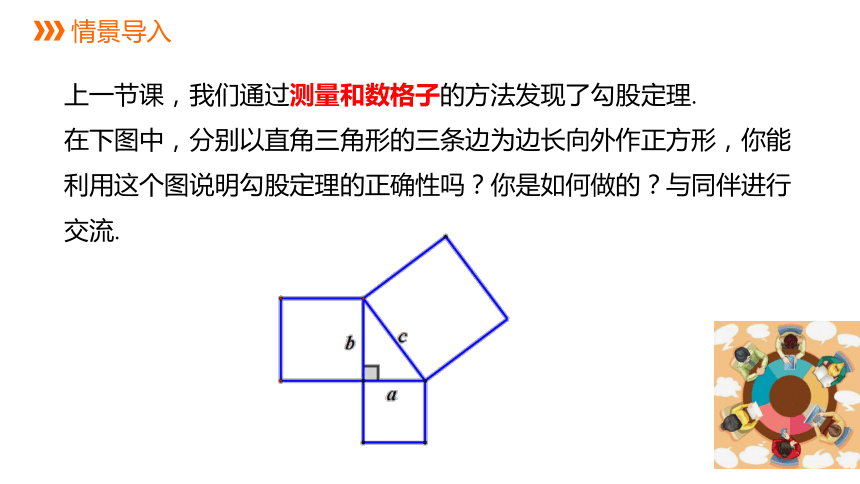
上一节课,我们通过测量和数格子的方法发现了勾股定理.
在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
情景导入
在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这幅图说明勾股定理的正确性吗?
割
补
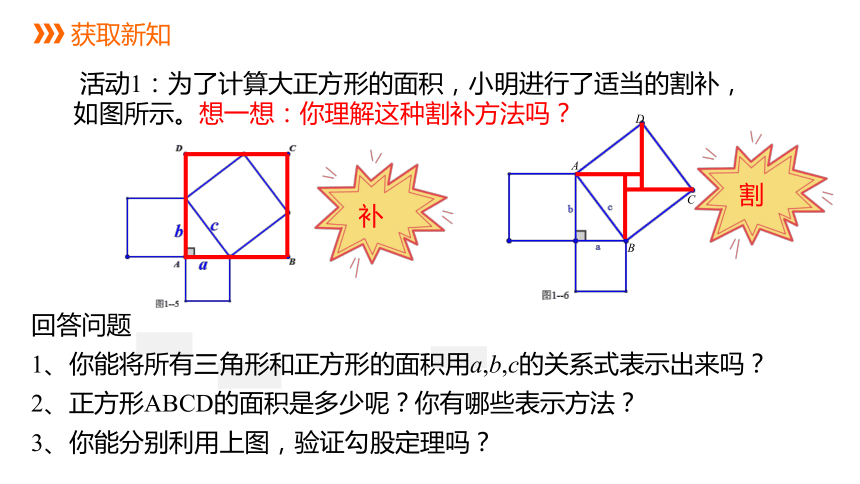
获取新知
活动1:为了计算大正方形的面积,小明进行了适当的割补,如图所示。想一想:你理解这种割补方法吗?
A
B
C
D
补
割
回答问题
1、你能将所有三角形和正方形的面积用a,b,c的关系式表示出来吗?
2、正方形ABCD的面积是多少呢?你有哪些表示方法?
3、你能分别利用上图,验证勾股定理吗?
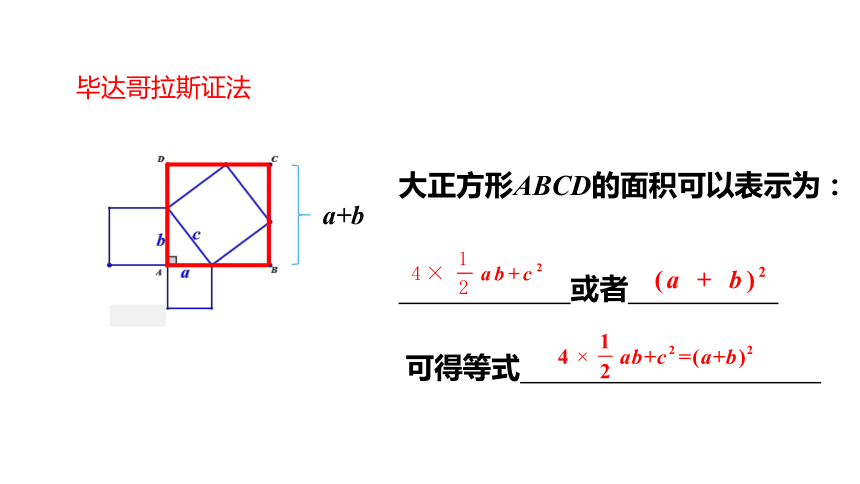
毕达哥拉斯证法
a+b
大正方形ABCD的面积可以表示为:
或者
可得等式
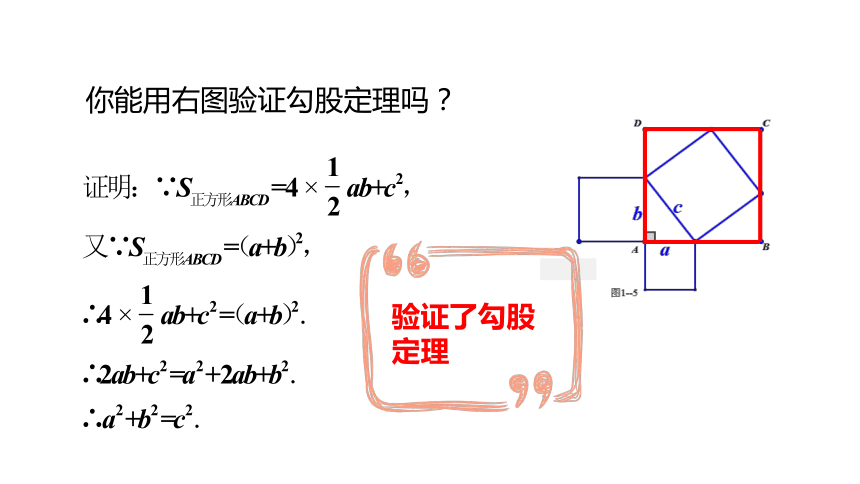
你能用右图验证勾股定理吗?
验证了勾股定理
赵爽弦图
A
B
C
D
小正方形ABCD的面积可以表示为:
或者
可得等式
你能用右图验证勾股定理吗?
A
B
C
D
也验证了勾股定理
美国总统证法
1876年,美国总统伽菲尔德(James Abram Garfield)利用下图证明了勾股定理,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系.
利用面积法证明
割补法是几何证明题中常用的方法,要注意这种方法的应用.你还能用其他方法证明勾股定理吗?
点击播放
例题讲解
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速公路,已知沿江高速公路的建设成本为5 000万元/km,该沿江高速公路的造价预计是多少?
30 km
40 km
50 km
120 km
课堂小结
勾股定理的验证方法
随堂演练
1.如图1-1,一棵高为8 m的大树被台风刮断,若树在离地面3 m的点C处折断,则树顶端落在离树底部( )
A.4 m处 B.5 m处 C.6 m处 D.7 m处
2.如图1-2,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,他们仅仅少走了 m路,却踩伤了花草( )
A.1 B.2 C.5 D.12
图1-1
图1-2
A
B
3.如图1-1-17,在海上观察所A,我边防海警发现正北方向5 km的B处有一可疑船只正在向正东方向12 km的C处行驶, 我边防海警立刻派船前往C处拦截.若可疑船只的行驶速度为60 km/h,则我边防海警船的速度至少为多少时,才能恰好在C处将可疑船只截住
解:由勾股定理,可以得到AC2=AB2+BC2,
即AC2=52+122,所以AC=13,可疑船只从B到C的时间为12÷60=0.2(h),所以我边防海警船的速度为13÷0.2=65(km/h)
答:我边防海警船的速度至少为65 km/h时,才能恰好在C处将可疑船只截住.
4.一辆装满货物的车,其外形高25m,宽1.6m,要开进厂门形状如图所示的某工厂,厂门上部为半圆形,下部为长方形,已知长方形的宽为2m,高为23m,半圆的直径与门的宽相等.这辆车能否通过该工厂的厂门 请说明理由.
解:能.
理由:如图,AB为半圆的直径,O为圆心,在AB上取一点D,使OD=0.8m.过点D作CH⊥AB,交半圆于点C,交门的底部于点H.
在Rt△OCD中,∠CDO=90°,OC=1m, OD=0.8m,由勾股定理得CD2=OC2-OD2=12-0.82=0.36,
所以CD=0.6(m).
所以CH=CD+DH=0.6+2.3=2.9(m)>2.5m.
所以这辆车能通过该工厂的厂门.
1.1 第2课时勾股定理的验证及其简单应用
第一章 勾股定理
知识回顾
勾股定理
在Rt△ABC 中,若直角边长分别是a,b,斜边长是c,
则:
这个定理叫做:勾股定理
上一节课,我们通过测量和数格子的方法发现了勾股定理.
在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
情景导入
在下图中,分别以直角三角形的三条边为边长向外作正方形,你能利用这幅图说明勾股定理的正确性吗?
割
补
获取新知
活动1:为了计算大正方形的面积,小明进行了适当的割补,如图所示。想一想:你理解这种割补方法吗?
A
B
C
D
补
割
回答问题
1、你能将所有三角形和正方形的面积用a,b,c的关系式表示出来吗?
2、正方形ABCD的面积是多少呢?你有哪些表示方法?
3、你能分别利用上图,验证勾股定理吗?
毕达哥拉斯证法
a+b
大正方形ABCD的面积可以表示为:
或者
可得等式
你能用右图验证勾股定理吗?
验证了勾股定理
赵爽弦图
A
B
C
D
小正方形ABCD的面积可以表示为:
或者
可得等式
你能用右图验证勾股定理吗?
A
B
C
D
也验证了勾股定理
美国总统证法
1876年,美国总统伽菲尔德(James Abram Garfield)利用下图证明了勾股定理,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系.
利用面积法证明
割补法是几何证明题中常用的方法,要注意这种方法的应用.你还能用其他方法证明勾股定理吗?
点击播放
例题讲解
如图是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速公路,已知沿江高速公路的建设成本为5 000万元/km,该沿江高速公路的造价预计是多少?
30 km
40 km
50 km
120 km
课堂小结
勾股定理的验证方法
随堂演练
1.如图1-1,一棵高为8 m的大树被台风刮断,若树在离地面3 m的点C处折断,则树顶端落在离树底部( )
A.4 m处 B.5 m处 C.6 m处 D.7 m处
2.如图1-2,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,他们仅仅少走了 m路,却踩伤了花草( )
A.1 B.2 C.5 D.12
图1-1
图1-2
A
B
3.如图1-1-17,在海上观察所A,我边防海警发现正北方向5 km的B处有一可疑船只正在向正东方向12 km的C处行驶, 我边防海警立刻派船前往C处拦截.若可疑船只的行驶速度为60 km/h,则我边防海警船的速度至少为多少时,才能恰好在C处将可疑船只截住
解:由勾股定理,可以得到AC2=AB2+BC2,
即AC2=52+122,所以AC=13,可疑船只从B到C的时间为12÷60=0.2(h),所以我边防海警船的速度为13÷0.2=65(km/h)
答:我边防海警船的速度至少为65 km/h时,才能恰好在C处将可疑船只截住.
4.一辆装满货物的车,其外形高25m,宽1.6m,要开进厂门形状如图所示的某工厂,厂门上部为半圆形,下部为长方形,已知长方形的宽为2m,高为23m,半圆的直径与门的宽相等.这辆车能否通过该工厂的厂门 请说明理由.
解:能.
理由:如图,AB为半圆的直径,O为圆心,在AB上取一点D,使OD=0.8m.过点D作CH⊥AB,交半圆于点C,交门的底部于点H.
在Rt△OCD中,∠CDO=90°,OC=1m, OD=0.8m,由勾股定理得CD2=OC2-OD2=12-0.82=0.36,
所以CD=0.6(m).
所以CH=CD+DH=0.6+2.3=2.9(m)>2.5m.
所以这辆车能通过该工厂的厂门.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
